【2023版】人教版数学八上-第13章 轴对称 13.3.1 第2课时 等腰三角形的判定 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第13章 轴对称 13.3.1 第2课时 等腰三角形的判定 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览






文档简介
(共28张PPT)
13.3.1第2课时 等腰三角形的判定
第十三章 轴对称
必
●
知识要点全练
夯实基础
000000000000000000000000000000000000
知识点1
等腰三角形的判定
1.如图,已知OC平分∠AOB,CD∥OB.若
OD=3cm,则CD等于
(A)
A.3 cm
B.4 cm
C.1,5 cm
B
D.2 cm
2.(2022·广州)如图,点D,E在人ABC的边
BC上,∠B=∠C,BD=CE,求证:△ABD
≌ACE.
证明:。∠B=∠C,。AB=
AC,在△ABD和△ACE
AB=AC,
B
D
E
中∠B=∠C,
BD=CE,
.'.△ABD2△ACE(SAS).
知识点2
等腰三角形性质与判定的综合应用
3.在下列三角形中,若AB=AC,则不能被一条
直线分成两个小等腰三角形的是
(B)
436
A
45°
108
B
B
B
B
A
B
C
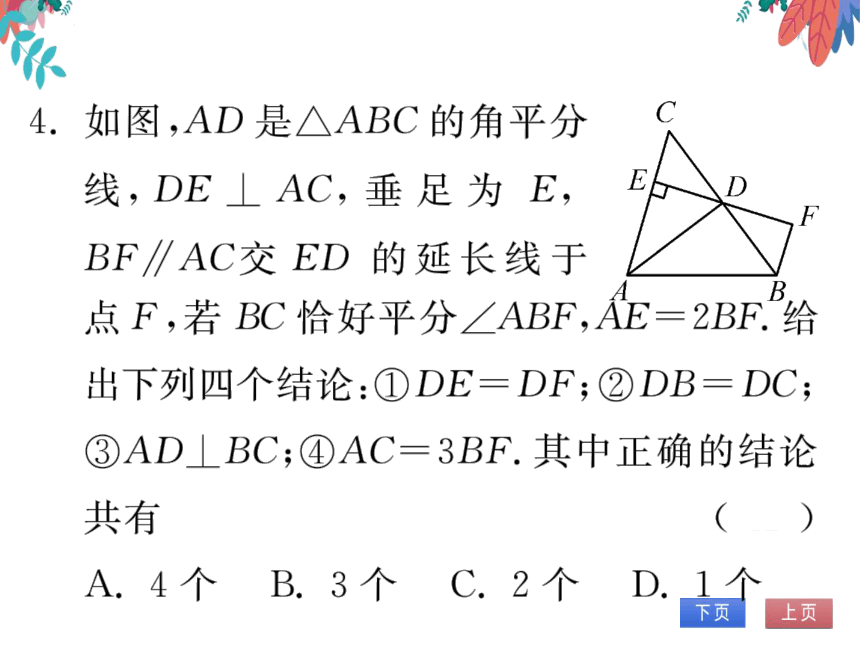
4.如图,AD是△ABC的角平分
线,DEAC,垂足为E,
BF∥AC交ED的延长线于
点F,若BC恰好平分∠ABF,AE=2BF.给
出下列四个结论:①DE=DF;②DB=DC;
③AD⊥BC;④AC=3BF.其中正确的结论
共有
(A)
A.4个
B.3个
C.2个
D.1个
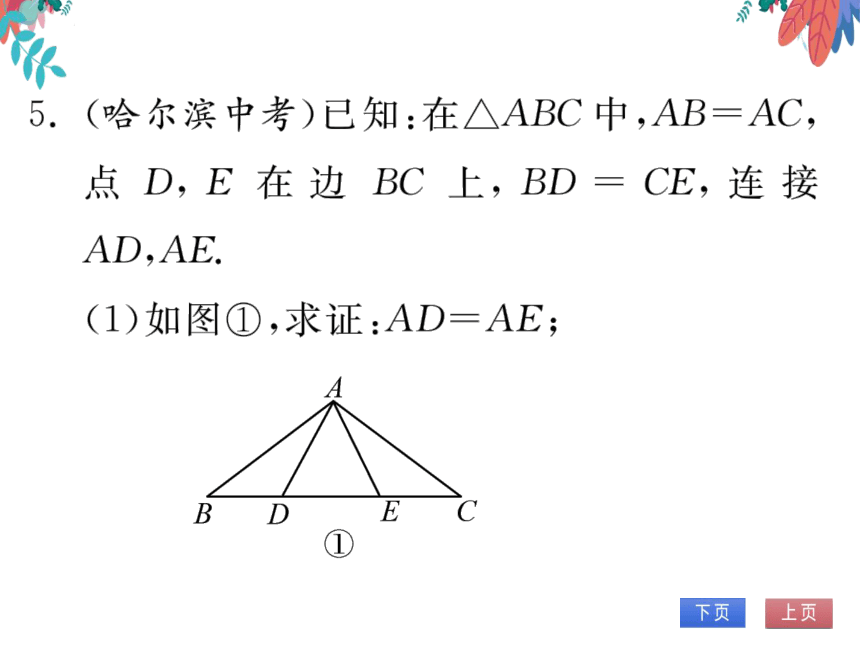
5.(哈尔滨中考)已知:在△ABC中,AB=AC,
点D,E在边BC上,BD=CE,连接
AD,AE.
(1)如 ①,求证:AD=AE;
A
B
D
E
C
B
D
E
C
①
今
2
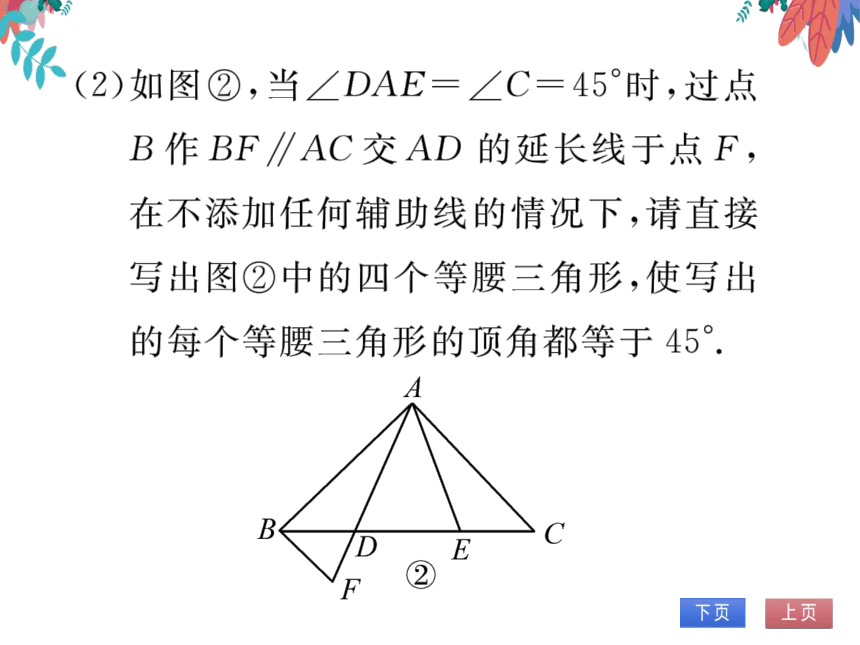
(2)如图②,当∠DAE=∠C=45°时,过点
B作BF∥AC交AD的延长线于点F,
在不添加任何辅助线的情况下,请直接
写出图②中的四个等腰三角形,使写出
的每个等腰三角形的顶角都等于45°.
(1)证明:,AB=AC,.∠D=∠C
在个ABD和△ACE中,
AB=AC,
∠B=∠C,.△ABD2△ACE(SAS).
BD=CE.
。。AD=AE.
(2)解:.AD=AE,.∠ADE=∠AED.
.BF∥AC,.∠FBD=∠C=45..'∠ABC=∠C=∠DAE
=45°,∠DDF=∠ADE,
·.∠F=∠BDF,∠BEA=∠BAE,∠CDA=∠CAD,
'.满足条件的等腰三角形有:人ABE,△ACD,△DAE,
△DBF.
知识点3用尺规作等腰三角形
6.已知线段a和∠a(如图),求作△ABC,使
AB=AC=a,∠A=∠.(保留作图痕迹,不
写作法)
解:△ABC如图所示.
13.3.1第2课时 等腰三角形的判定
第十三章 轴对称
必
●
知识要点全练
夯实基础
000000000000000000000000000000000000
知识点1
等腰三角形的判定
1.如图,已知OC平分∠AOB,CD∥OB.若
OD=3cm,则CD等于
(A)
A.3 cm
B.4 cm
C.1,5 cm
B
D.2 cm
2.(2022·广州)如图,点D,E在人ABC的边
BC上,∠B=∠C,BD=CE,求证:△ABD
≌ACE.
证明:。∠B=∠C,。AB=
AC,在△ABD和△ACE
AB=AC,
B
D
E
中∠B=∠C,
BD=CE,
.'.△ABD2△ACE(SAS).
知识点2
等腰三角形性质与判定的综合应用
3.在下列三角形中,若AB=AC,则不能被一条
直线分成两个小等腰三角形的是
(B)
436
A
45°
108
B
B
B
B
A
B
C
4.如图,AD是△ABC的角平分
线,DEAC,垂足为E,
BF∥AC交ED的延长线于
点F,若BC恰好平分∠ABF,AE=2BF.给
出下列四个结论:①DE=DF;②DB=DC;
③AD⊥BC;④AC=3BF.其中正确的结论
共有
(A)
A.4个
B.3个
C.2个
D.1个
5.(哈尔滨中考)已知:在△ABC中,AB=AC,
点D,E在边BC上,BD=CE,连接
AD,AE.
(1)如 ①,求证:AD=AE;
A
B
D
E
C
B
D
E
C
①
今
2
(2)如图②,当∠DAE=∠C=45°时,过点
B作BF∥AC交AD的延长线于点F,
在不添加任何辅助线的情况下,请直接
写出图②中的四个等腰三角形,使写出
的每个等腰三角形的顶角都等于45°.
(1)证明:,AB=AC,.∠D=∠C
在个ABD和△ACE中,
AB=AC,
∠B=∠C,.△ABD2△ACE(SAS).
BD=CE.
。。AD=AE.
(2)解:.AD=AE,.∠ADE=∠AED.
.BF∥AC,.∠FBD=∠C=45..'∠ABC=∠C=∠DAE
=45°,∠DDF=∠ADE,
·.∠F=∠BDF,∠BEA=∠BAE,∠CDA=∠CAD,
'.满足条件的等腰三角形有:人ABE,△ACD,△DAE,
△DBF.
知识点3用尺规作等腰三角形
6.已知线段a和∠a(如图),求作△ABC,使
AB=AC=a,∠A=∠.(保留作图痕迹,不
写作法)
解:△ABC如图所示.
