【2023版】人教版数学八上-第13章 轴对称 专题训练(五)轴对称经典解答题 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第13章 轴对称 专题训练(五)轴对称经典解答题 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览






文档简介
(共29张PPT)
专题训练(五) 轴对称经典解答题
第十三章 轴对称
必
●
类型1“平行线、角平分线、等腰三角形”模型
1.如图,在△ABC中,∠BAC=90°,ADBC
于点D,∠ACB的平分线交AD于点E,交
AB于点F,FG⊥BC于点G.求证:
AE
-FG.
。。∠AFC=∠DEC
又.∠AEF=∠DEC,
。。∠AFC=∠AEF.
。°。AE=FA。。。AE=FG.
证明:.CF平分∠ACB,
∠BAC=90°,FG⊥BC,
B
.∠ACF=∠ECD,
FG=FA.
.∠AFC+∠ACF=90°,
∠DEC十∠ECD=90°,
2.如图,在△ABC中,AD平分∠BAC交BC
于点D,点E,F分别在BD,AD上,EF∥
AB,且DE=CD.求证:EF=AC.
证明:如图,延长AD
到G使DG=FD,并连
分
接CG.
B
E
证明:如图,延长AD
到G使DG=FD,并连
F
接CG.
B
E
在△EFD和△CGD中,
DE-CD,
∠EDF=∠CDG,
FD=DG,
在人ED和人△CGD中,
DE=CD,
∠EDF=∠CDG,
FD=DG.
.'.∧EFD≌∧CGD(SAS).
。∠EFG=∠G,EF=CG.
.EF∥AD,.∠EFG=∠DAD.
又.AD平分∠DAC,
,.∠BAD=∠CAD.
。∠CAD=∠G.'.AC=CG.
。'。EF=AC.
类型2构造等腰三角形
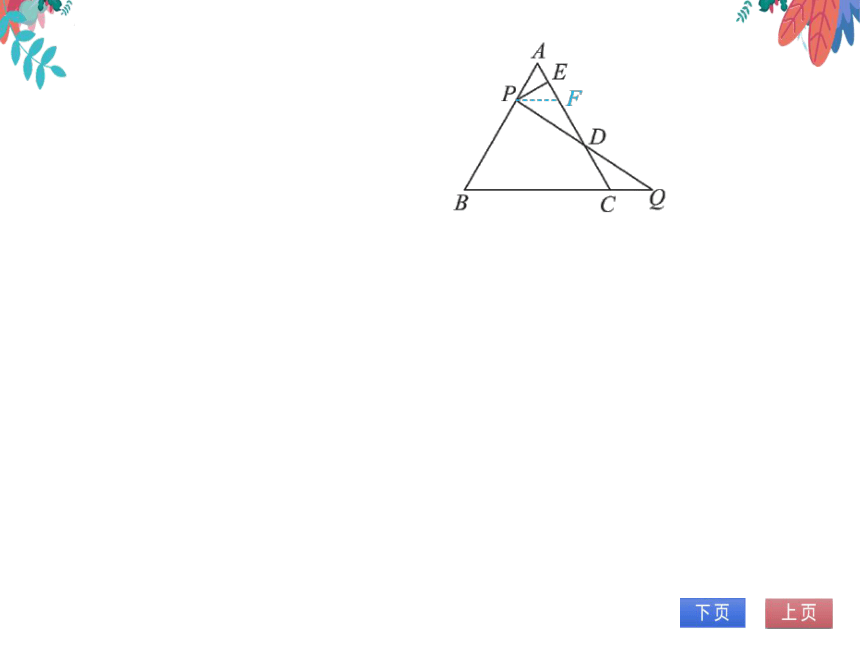
3.如图,过等边△ABC的边AB上一点P,作
PEAC于点E,Q为BC延长线的一点,
且PA=CQ,连PQ交AC边于D.
(1)求证:PD=DQ;
(2)若△ABC的边长为1,求DE的长.
。。/AFP=60°,
°。人APF是等边三角形。
。。AP=PF.
。AP=CQ..。PF=CQ.
.人PFD≌人QCD(ASA)..'.PD=DQ.
(1)证明:如图.过点P作
PF∥BC交AC于点F,
.'。∠AFP=∠ACB,∠FPD
=∠Q,∠PFD=∠QCD.
B
C
。°入AC为等边三角形,
..∠A=∠ACB=60°.
(2)解:,△APF是等边三角形,PEAC,
'.AE=EF=AF,由(1)知△PFD≌△OCD,
∴.CD=DF=
CF.
2
DE-BF+DF-(AK+CE)-TAC.
又AC=1,DE=
21
4.已知△ABC为等边三角形,点D为AC上的
一个动点,点E为BC延长线上一点.
(1)如图①,若点D在AC上,延长BC至
E,使CE=AD,DGBC于G.求证:
BG=EG;
专题训练(五) 轴对称经典解答题
第十三章 轴对称
必
●
类型1“平行线、角平分线、等腰三角形”模型
1.如图,在△ABC中,∠BAC=90°,ADBC
于点D,∠ACB的平分线交AD于点E,交
AB于点F,FG⊥BC于点G.求证:
AE
-FG.
。。∠AFC=∠DEC
又.∠AEF=∠DEC,
。。∠AFC=∠AEF.
。°。AE=FA。。。AE=FG.
证明:.CF平分∠ACB,
∠BAC=90°,FG⊥BC,
B
.∠ACF=∠ECD,
FG=FA.
.∠AFC+∠ACF=90°,
∠DEC十∠ECD=90°,
2.如图,在△ABC中,AD平分∠BAC交BC
于点D,点E,F分别在BD,AD上,EF∥
AB,且DE=CD.求证:EF=AC.
证明:如图,延长AD
到G使DG=FD,并连
分
接CG.
B
E
证明:如图,延长AD
到G使DG=FD,并连
F
接CG.
B
E
在△EFD和△CGD中,
DE-CD,
∠EDF=∠CDG,
FD=DG,
在人ED和人△CGD中,
DE=CD,
∠EDF=∠CDG,
FD=DG.
.'.∧EFD≌∧CGD(SAS).
。∠EFG=∠G,EF=CG.
.EF∥AD,.∠EFG=∠DAD.
又.AD平分∠DAC,
,.∠BAD=∠CAD.
。∠CAD=∠G.'.AC=CG.
。'。EF=AC.
类型2构造等腰三角形
3.如图,过等边△ABC的边AB上一点P,作
PEAC于点E,Q为BC延长线的一点,
且PA=CQ,连PQ交AC边于D.
(1)求证:PD=DQ;
(2)若△ABC的边长为1,求DE的长.
。。/AFP=60°,
°。人APF是等边三角形。
。。AP=PF.
。AP=CQ..。PF=CQ.
.人PFD≌人QCD(ASA)..'.PD=DQ.
(1)证明:如图.过点P作
PF∥BC交AC于点F,
.'。∠AFP=∠ACB,∠FPD
=∠Q,∠PFD=∠QCD.
B
C
。°入AC为等边三角形,
..∠A=∠ACB=60°.
(2)解:,△APF是等边三角形,PEAC,
'.AE=EF=AF,由(1)知△PFD≌△OCD,
∴.CD=DF=
CF.
2
DE-BF+DF-(AK+CE)-TAC.
又AC=1,DE=
21
4.已知△ABC为等边三角形,点D为AC上的
一个动点,点E为BC延长线上一点.
(1)如图①,若点D在AC上,延长BC至
E,使CE=AD,DGBC于G.求证:
BG=EG;
