【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.2.1 平方差公式 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.2.1 平方差公式 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:08 | ||
图片预览






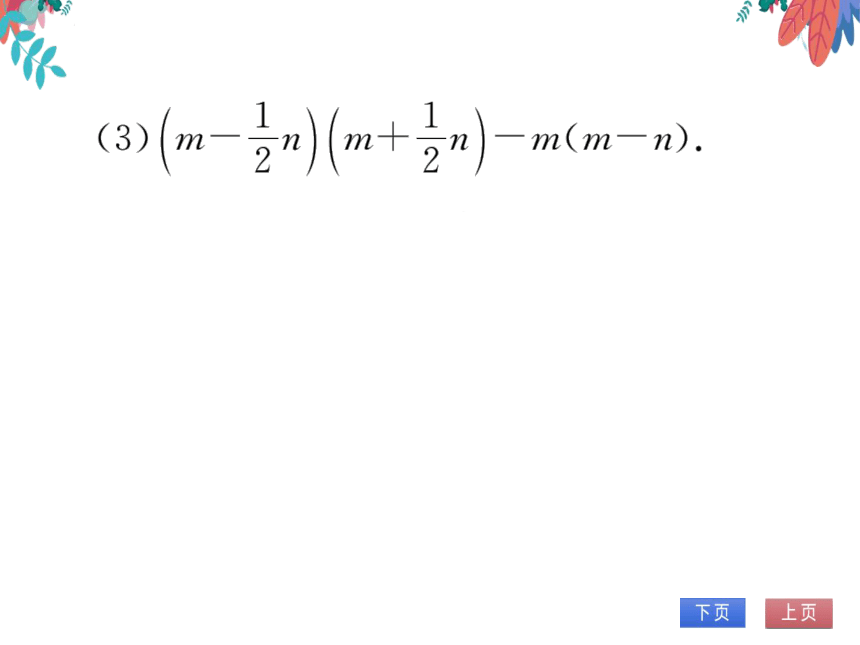

文档简介
(共21张PPT)
14.2.1 平方差公式
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
平方差公式
1.在下列多项式的乘法中,可以用平方差公
式进行计算的是
(B)
A.(x+1)(1+x)
B.(gatbjio-za)
C.(-a+b)(a-b)D.(x2-y)(x+y2)
2.(2022春·新城区校级期中)下列等式成立
的是
(C)
A.(-x-1)(-x-1)=x2-2x+1
B.(-x+1)(-x十1)=-x2-2x+1
C.(1+x)(-x十1)=1-x2
D.(-x+1)(-x-1)=-x2-1
3.下列计算正确的是
CC
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a十3b)=a2-9b2
4.填空:
(1)(2x-3y)·(2x+3y)=4.x2-9y;
(2)(-m-n)·(-m+n)=m2-n2.
5.(2022春·铁岭期中)若a2一b=一72,a一
b=12,则a+b的值为:
一6
6.计算:
(1)(xy+5)(xy-5);
解:原式=(xy)2一52=x2y2一25.
(2)(-4a+3)(-4a-3);
解:原式=(一4a)2一32=16a2一9.
()m-mm-n).
解:原式=m2-(2)-m2+mn
mn
知识点2平方差公式的几何意义
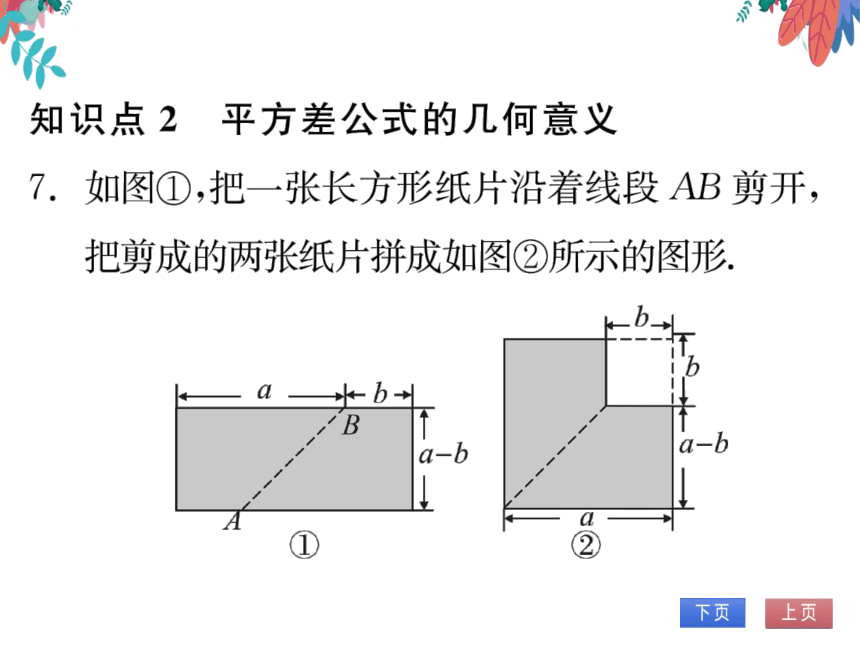
7.如图①,把一张长方形纸片沿着线段AB剪开,
把剪成的两张纸片拼成如图②所示的图形
b
a-b
①
(1)设图①中阴影部分面积为S1,图②中阴
影部分面积为S2,请直接用含,b的式
子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
解:(1)S1=(a+b)(a-b),S2=a2-b2.
(2)(a+b)(a-b)=a2-b2.
知识点3平方差公式的运用
8.运用平方差公式简便计算:
(1)9.8×10.2;
解:原式=(10一0.2)X(10+0.2)
=102一0,22
=99.96.
(2)129×127-1282.
解:原式=(128+1)X(128一1)一1282
=1282一1一1282
=一1。
规律方法全练
提升能力
000000000000000000000000000000000000
9.(2021春·武宣县期中)若x十y一5十
(x一y一3)2=0,则x2一y2的结果是(C)
A.2
B.8
C.15
D.16
14.2.1 平方差公式
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
平方差公式
1.在下列多项式的乘法中,可以用平方差公
式进行计算的是
(B)
A.(x+1)(1+x)
B.(gatbjio-za)
C.(-a+b)(a-b)D.(x2-y)(x+y2)
2.(2022春·新城区校级期中)下列等式成立
的是
(C)
A.(-x-1)(-x-1)=x2-2x+1
B.(-x+1)(-x十1)=-x2-2x+1
C.(1+x)(-x十1)=1-x2
D.(-x+1)(-x-1)=-x2-1
3.下列计算正确的是
CC
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a十3b)=a2-9b2
4.填空:
(1)(2x-3y)·(2x+3y)=4.x2-9y;
(2)(-m-n)·(-m+n)=m2-n2.
5.(2022春·铁岭期中)若a2一b=一72,a一
b=12,则a+b的值为:
一6
6.计算:
(1)(xy+5)(xy-5);
解:原式=(xy)2一52=x2y2一25.
(2)(-4a+3)(-4a-3);
解:原式=(一4a)2一32=16a2一9.
()m-mm-n).
解:原式=m2-(2)-m2+mn
mn
知识点2平方差公式的几何意义
7.如图①,把一张长方形纸片沿着线段AB剪开,
把剪成的两张纸片拼成如图②所示的图形
b
a-b
①
(1)设图①中阴影部分面积为S1,图②中阴
影部分面积为S2,请直接用含,b的式
子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
解:(1)S1=(a+b)(a-b),S2=a2-b2.
(2)(a+b)(a-b)=a2-b2.
知识点3平方差公式的运用
8.运用平方差公式简便计算:
(1)9.8×10.2;
解:原式=(10一0.2)X(10+0.2)
=102一0,22
=99.96.
(2)129×127-1282.
解:原式=(128+1)X(128一1)一1282
=1282一1一1282
=一1。
规律方法全练
提升能力
000000000000000000000000000000000000
9.(2021春·武宣县期中)若x十y一5十
(x一y一3)2=0,则x2一y2的结果是(C)
A.2
B.8
C.15
D.16
