【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.1.4 第4课时 整式的除法 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.1.4 第4课时 整式的除法 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
14.1.4第4课时 整式的除法
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
同底数幂的除法
1.计算(-3a3)2÷a2的结果是
D
A.-9a4B.6a4
C.9a3
D.9a
2.(2022·黄石)下列运算正确的是
(D)
A.a9-a7=a2
B.a6÷a3=a2
C.a2。a3=a6
D.(-2a2b)2=4a4b2
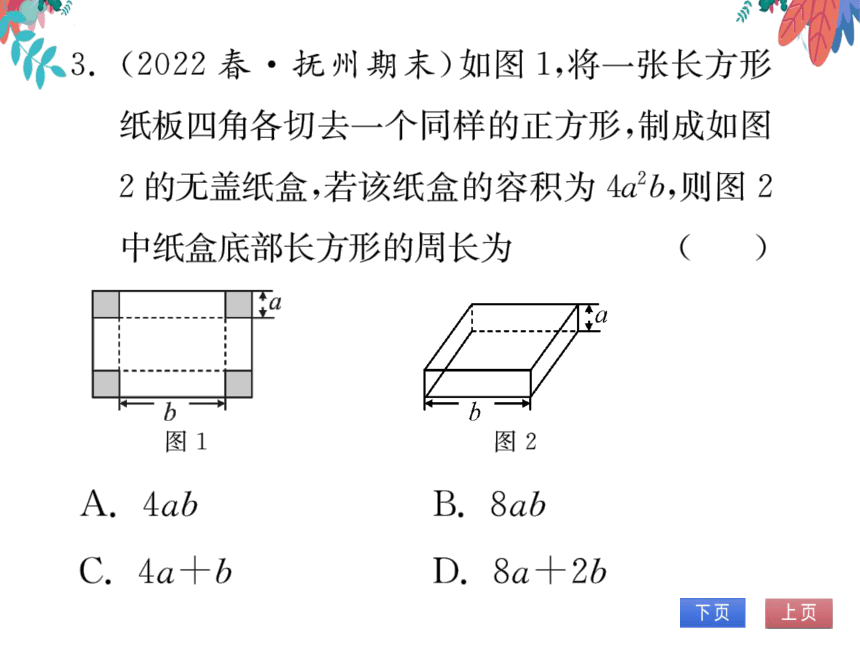
3.(2022春·抚州期末)如图1,将一张长方形
纸板四角各切去一个同样的正方形,制成如图
2的无盖纸盒,若该纸盒的容积为4αb,则图2
中纸盒底部长方形的周长为
a
o
b
b
图1
图2
4.(教材Po3例7变式)计算:
(1)(-a)6÷(-a)2;
解:原式=(一a)4=a4;
(2)(x-y)7÷(y-x);
解:原式=x一y;
(3)(-mn)5÷(-mn)3.
解:原式=(一mn)2=mn2.
知识点20次幂
5.(2022·山东济宁)下列各式运算正确的是(C)
A.-3(x-y)=-3x+y
B.x3·x2=x6
C.(π-3.14)0=1
D.(x3)2=x5
6.若(a一3)°=1,则a的取值范围是
(D)
A.a>3
B.a<3
C.a=3
D.a≠3
知识点3整式的除法
8.(2021·青岛)计算6m÷(一2m)3的结果为
(D)
3
A.-
3
2
B.-1
C.
D.
4
4
9.计算(5m2+15m3n-20m4)÷(-5m2)的结
果是
(C)
A.1-3mn+4m2
B.-1-3m+4m
C.4m2-3mn-1
D.4m2-3mn
10.(2022春·宝安区校级期中)已知10m=
8
2,10”=3,则103m-2n=
9
11.计算:
(1)-24a3b3÷4ab2:
解:原式=(一24÷4)a3-1b3-2
=-6a2b.
2)8x÷(7y:
解:原式=〔-8÷2xy1
=一16y.
(3)(12x3-8x2+16x)÷(-4x);
解:原式=(一12÷4)x3-1十(8÷4)x2-1十
(-16÷4)x1-1
=一3x2十2x一4.
45a6-a61:a6}
解:原式=(306-)a÷)b
=6a2b3一b2,
规律方法全练
提升能力
000000000000000000000000000000000000
12.已知8a3bm÷8a"b2=b,那么m,n的取值
为
(A)
A.m=4,n=3
B.m=4,n=1
C.m=1,n=3
D.m=2,n=3
14.1.4第4课时 整式的除法
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
同底数幂的除法
1.计算(-3a3)2÷a2的结果是
D
A.-9a4B.6a4
C.9a3
D.9a
2.(2022·黄石)下列运算正确的是
(D)
A.a9-a7=a2
B.a6÷a3=a2
C.a2。a3=a6
D.(-2a2b)2=4a4b2
3.(2022春·抚州期末)如图1,将一张长方形
纸板四角各切去一个同样的正方形,制成如图
2的无盖纸盒,若该纸盒的容积为4αb,则图2
中纸盒底部长方形的周长为
a
o
b
b
图1
图2
4.(教材Po3例7变式)计算:
(1)(-a)6÷(-a)2;
解:原式=(一a)4=a4;
(2)(x-y)7÷(y-x);
解:原式=x一y;
(3)(-mn)5÷(-mn)3.
解:原式=(一mn)2=mn2.
知识点20次幂
5.(2022·山东济宁)下列各式运算正确的是(C)
A.-3(x-y)=-3x+y
B.x3·x2=x6
C.(π-3.14)0=1
D.(x3)2=x5
6.若(a一3)°=1,则a的取值范围是
(D)
A.a>3
B.a<3
C.a=3
D.a≠3
知识点3整式的除法
8.(2021·青岛)计算6m÷(一2m)3的结果为
(D)
3
A.-
3
2
B.-1
C.
D.
4
4
9.计算(5m2+15m3n-20m4)÷(-5m2)的结
果是
(C)
A.1-3mn+4m2
B.-1-3m+4m
C.4m2-3mn-1
D.4m2-3mn
10.(2022春·宝安区校级期中)已知10m=
8
2,10”=3,则103m-2n=
9
11.计算:
(1)-24a3b3÷4ab2:
解:原式=(一24÷4)a3-1b3-2
=-6a2b.
2)8x÷(7y:
解:原式=〔-8÷2xy1
=一16y.
(3)(12x3-8x2+16x)÷(-4x);
解:原式=(一12÷4)x3-1十(8÷4)x2-1十
(-16÷4)x1-1
=一3x2十2x一4.
45a6-a61:a6}
解:原式=(306-)a÷)b
=6a2b3一b2,
规律方法全练
提升能力
000000000000000000000000000000000000
12.已知8a3bm÷8a"b2=b,那么m,n的取值
为
(A)
A.m=4,n=3
B.m=4,n=1
C.m=1,n=3
D.m=2,n=3
