【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.2.2 第1课时 完全平方公式 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第14章 整式的乘法与因式分解 14.2.2 第1课时 完全平方公式 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:08 | ||
图片预览







文档简介
(共21张PPT)
14.2.2第1课时 完全平方公式
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
完全平方公式
1.(2022·沈阳)下列计算结果正确的是
D
A.(a3)3=a6
B.a6÷a3=a2
C.(ab)2-ab8
D.(a十b)2=a2+2ab+b2
2.(2021·广西来宾)计算(2x一1)(1一2x)结
果正确的是
(C)
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
3.若(y十a)2=y2-6y+b,则a,b的值分别为
(D)
A.a=3,b=9
B.a=-3,b=-9
C.a=3,b=-9
D.a=-3,b=9
4.(原创题)若(2一x)2=m2一4x十x2,则m=
土2
5.计算:
(1)(3a+2b)2;
解:原式=9a2十12ab十4b.
知识点2:
完全平方公式的几何意义
6.如图,将完全相同的四个长方形纸片拼成
一个正方形,则可得出一个等式为
D
A.(a+b)2=a2+2ab+b2
b
b丑
B.(a-b)2=a2-2ab+b2
C.a2-b2=(a+b)(a-b)
D.(a十b)2=(a-b)2十4ab
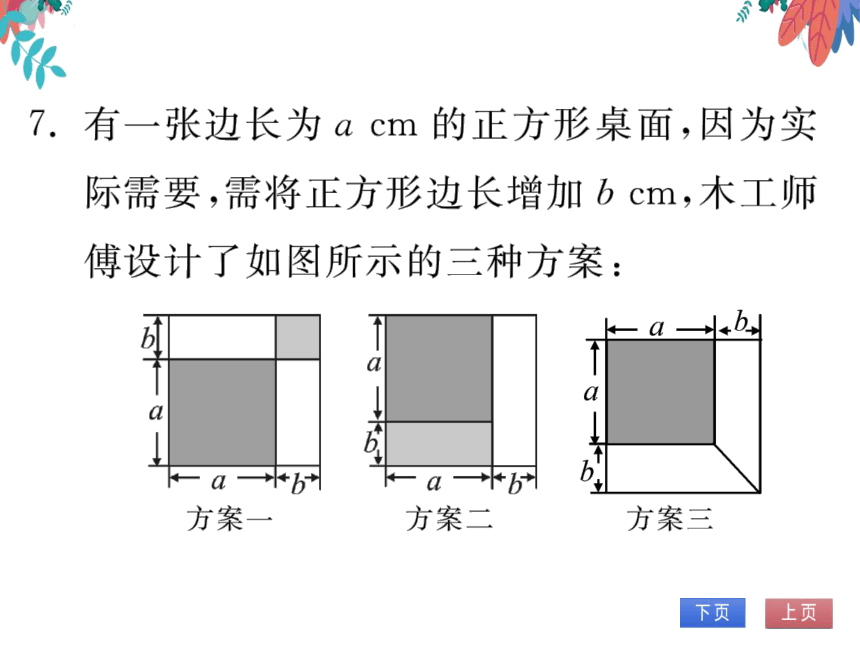
7.有一张边长为acm的正方形桌面,因为实
际需要,需将正方形边长增加bcm,木工师
傅设计了如图所示的三种方案:
a2剑
b
方案一
方案二
方案三
小明发现这三种方案都能验证公式:α2十
2ab+b2=(a+b)2.
对于方案一,小明是这样验证的:
a2+ab+ab+62=a2+2ab+82=(a+b)2.
请你根据方案二、方案三,写出公式的验证
过程.
解:方案二:a2+ab+(a十b)b=a2+ab+ab
+b2=a2+2ab+b2=(a+b)2.
方案三:d+[a+(a+b)]b+[a+(a+b)]b-d
2
2
+b+号6+b+6=r+2a6+i=(a+b郇,
知识点3
灵活运用完全平方公式计算
8.(2022春·碑林区校级期中)已知(α十
b)2=29,(a一b)2=13,则ab的值为(D)
A.42
B.16
C.8
D.4
9.(2022春·汉寿县期末)若x十y=3,xy=
一5,则(x一y)2=
29
规律方法全练
提升能力
000000000000000000000000000000000000
10.(2022春·北碚区校级期中)设a=x
2020,b=x-2022,c=x-2021,若a2十
b2=56,则c2=
(A)
A.27
B.24
C.22
D.
20
14.2.2第1课时 完全平方公式
第十四章 整式的乘法与因式分解
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
完全平方公式
1.(2022·沈阳)下列计算结果正确的是
D
A.(a3)3=a6
B.a6÷a3=a2
C.(ab)2-ab8
D.(a十b)2=a2+2ab+b2
2.(2021·广西来宾)计算(2x一1)(1一2x)结
果正确的是
(C)
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
3.若(y十a)2=y2-6y+b,则a,b的值分别为
(D)
A.a=3,b=9
B.a=-3,b=-9
C.a=3,b=-9
D.a=-3,b=9
4.(原创题)若(2一x)2=m2一4x十x2,则m=
土2
5.计算:
(1)(3a+2b)2;
解:原式=9a2十12ab十4b.
知识点2:
完全平方公式的几何意义
6.如图,将完全相同的四个长方形纸片拼成
一个正方形,则可得出一个等式为
D
A.(a+b)2=a2+2ab+b2
b
b丑
B.(a-b)2=a2-2ab+b2
C.a2-b2=(a+b)(a-b)
D.(a十b)2=(a-b)2十4ab
7.有一张边长为acm的正方形桌面,因为实
际需要,需将正方形边长增加bcm,木工师
傅设计了如图所示的三种方案:
a2剑
b
方案一
方案二
方案三
小明发现这三种方案都能验证公式:α2十
2ab+b2=(a+b)2.
对于方案一,小明是这样验证的:
a2+ab+ab+62=a2+2ab+82=(a+b)2.
请你根据方案二、方案三,写出公式的验证
过程.
解:方案二:a2+ab+(a十b)b=a2+ab+ab
+b2=a2+2ab+b2=(a+b)2.
方案三:d+[a+(a+b)]b+[a+(a+b)]b-d
2
2
+b+号6+b+6=r+2a6+i=(a+b郇,
知识点3
灵活运用完全平方公式计算
8.(2022春·碑林区校级期中)已知(α十
b)2=29,(a一b)2=13,则ab的值为(D)
A.42
B.16
C.8
D.4
9.(2022春·汉寿县期末)若x十y=3,xy=
一5,则(x一y)2=
29
规律方法全练
提升能力
000000000000000000000000000000000000
10.(2022春·北碚区校级期中)设a=x
2020,b=x-2022,c=x-2021,若a2十
b2=56,则c2=
(A)
A.27
B.24
C.22
D.
20
