2022-2023学年人教版九年级数学下册三视图练习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册三视图练习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 316.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览

文档简介
2022-2023学年人教版九年级数学下册三视图练习题
学校:___________姓名:___________班级:_____________
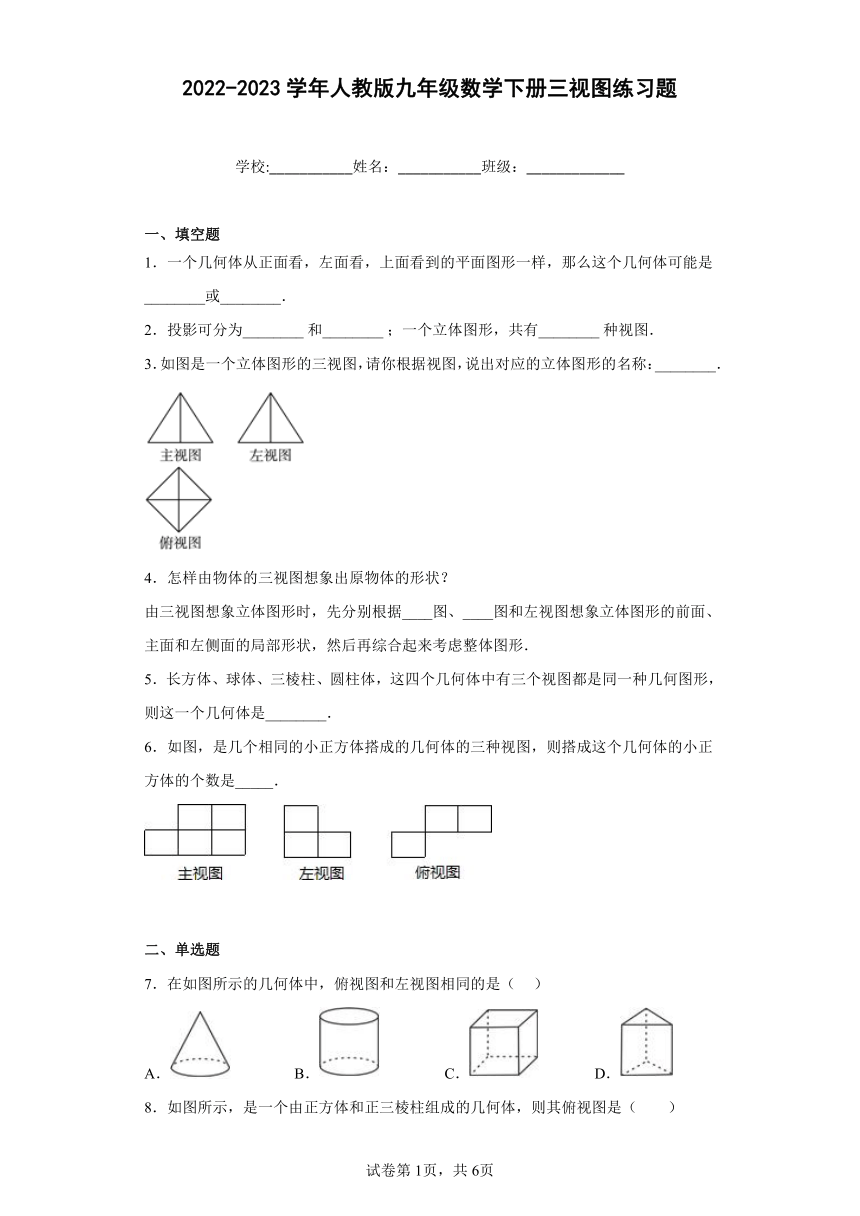
一、填空题
1.一个几何体从正面看,左面看,上面看到的平面图形一样,那么这个几何体可能是________或________.
2.投影可分为________ 和________ ;一个立体图形,共有________ 种视图.
3.如图是一个立体图形的三视图,请你根据视图,说出对应的立体图形的名称:________.
4.怎样由物体的三视图想象出原物体的形状?
由三视图想象立体图形时,先分别根据____图、____图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
5.长方体、球体、三棱柱、圆柱体,这四个几何体中有三个视图都是同一种几何图形,则这一个几何体是________.
6.如图,是几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是_____.
二、单选题
7.在如图所示的几何体中,俯视图和左视图相同的是( )
A. B. C. D.
8.如图所示,是一个由正方体和正三棱柱组成的几何体,则其俯视图是( )
A. B. C. D.
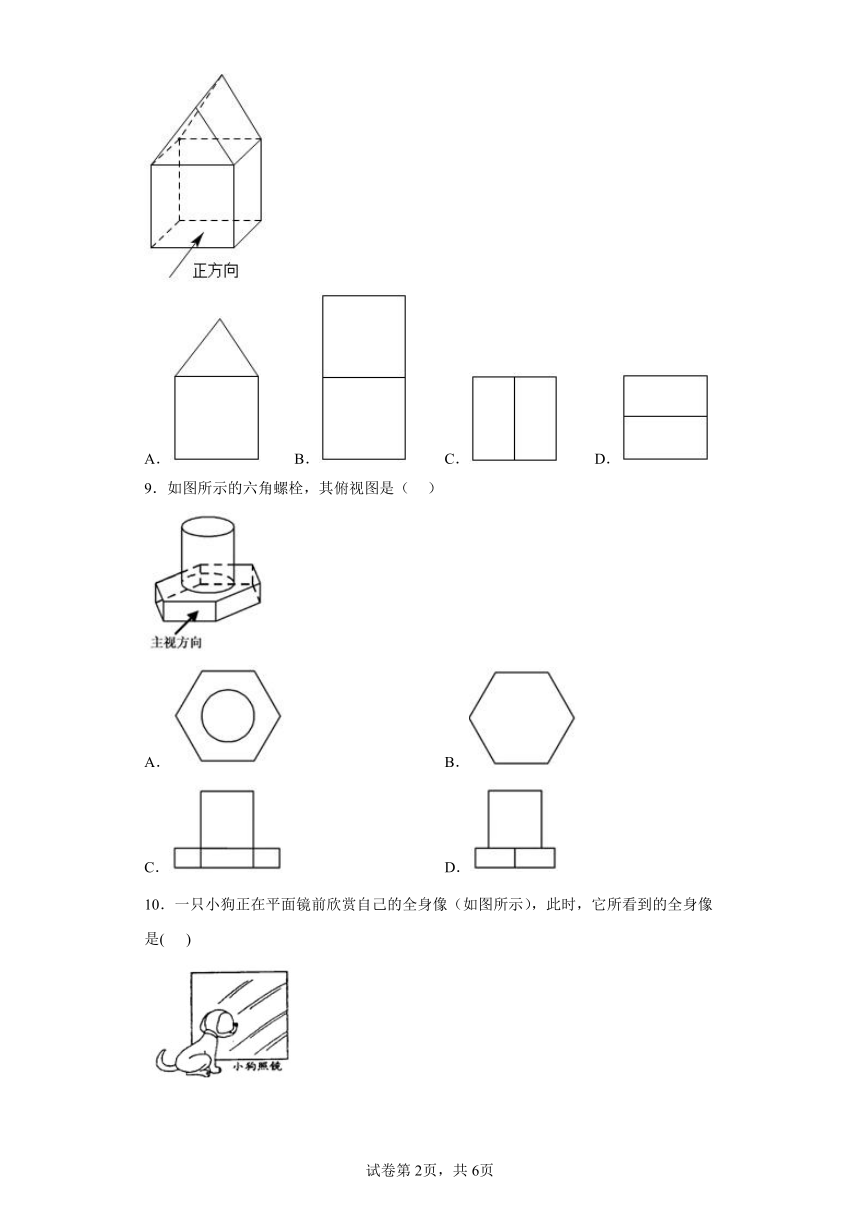
9.如图所示的六角螺栓,其俯视图是( )
A. B.
C. D.
10.一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是( )
A. B. C. D.
11.从正面看如图所示的正三棱柱,得到的平面图形是( )
A. B.
C. D.
12.如图所示的几何体的左视图为( )
A. B. C. D.
13.八个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
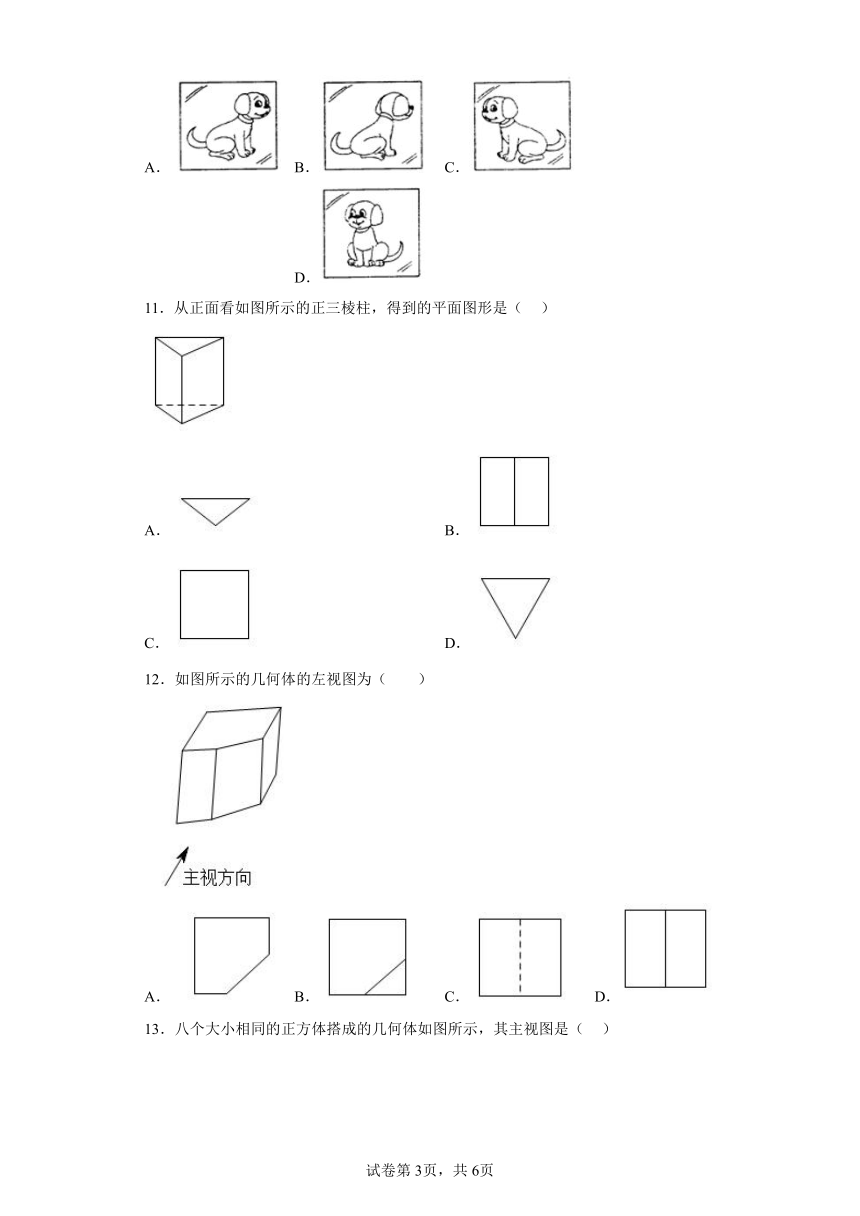
14.如图是一个立体图形的三视图,该立体图形是( )
A.长方体 B.正方体 C.三棱柱 D.圆柱
15.如图是某几何体的三视图,该几何体是( )
A.圆柱 B.五棱柱 C.长方体 D.五棱锥
16.如图中几何体从左面看能得到( )
A. B. C. D.
17.如图是一个几何体的三种视图,则该几何体可能是( )
A. B. C. D.
三、解答题
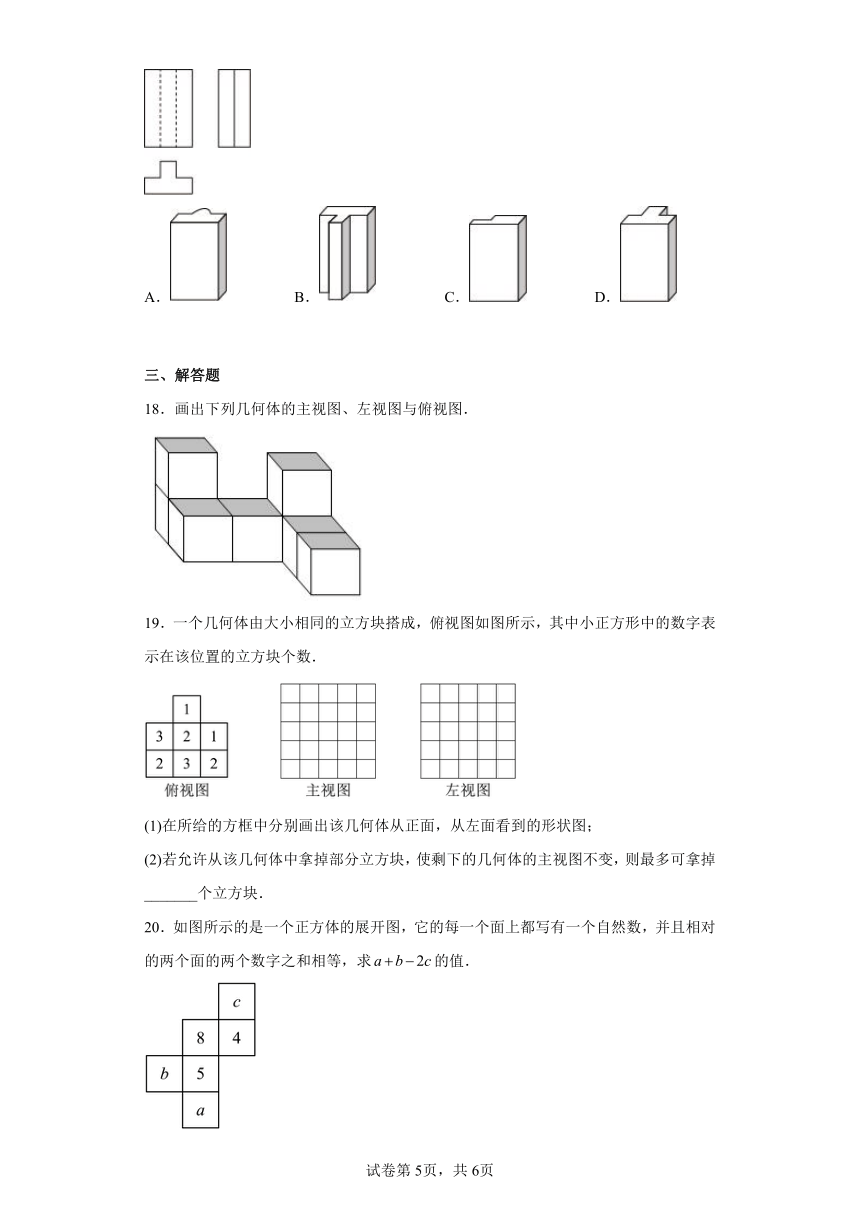
18.画出下列几何体的主视图、左视图与俯视图.
19.一个几何体由大小相同的立方块搭成,俯视图如图所示,其中小正方形中的数字表示在该位置的立方块个数.
(1)在所给的方框中分别画出该几何体从正面,从左面看到的形状图;
(2)若允许从该几何体中拿掉部分立方块,使剩下的几何体的主视图不变,则最多可拿掉_______个立方块.
20.如图所示的是一个正方体的展开图,它的每一个面上都写有一个自然数,并且相对的两个面的两个数字之和相等,求的值.
21.如图是由一些棱长都为的小正方体组合成的简单几何体.
(1)画出该几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加__________块小正方体.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 正方体 球
【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可.
【详解】正方体从正面看,左面看,上面看到的平面图形为全等的正方形;
球从正面看,左面看,上面看到的平面图形为全等的圆,
∴这个几何体可能是正方体或球.
【点睛】考查三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.
2. 平行投影 中心投影 三
【分析】根据投影的分类:平行投影与中心投影直接填写;根据立体图形三视图的概念直接填写即可.
【详解】投影可分为平行投影和中心投影;一个立体图形,共有三种视图.
【点睛】本题考查投影的分类及立体图形的三视图,属于最基础知识,牢记相关概念是解决问题的关键.
3.四棱锥
【分析】主视图、左视图、俯视图是分别别从物体正面、左面和上面看,所得到的图形,根据给出的三视图,分析判定出即可
【详解】根据题意,
从俯视图中知,这个立体图形有4条棱,底面为正方
形,而且主、左视图中三角形的面积相等,
因此,符合条件的几何体是四棱锥.
故答案为:四棱锥.
【点睛】此题考查由三视图判断几何体,难度不大
4. 主视 俯视
【解析】略
5.球体
【分析】视图是同一种几何图形的几何体是正方体或者球体,看本题所给选项中有哪种几何体即可.
【详解】视图是同一种几何图形的几何体是正方体或者球体,所给选项中有球体,
故答案为球体.
【点睛】考查三视图的知识;掌握常见几何体的三视图知识是解决本题的关键.
6.5
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】解:由主视图与左视图可以在俯视图上标注数字为:
主视图有三列,每列的方块数分别是:1,2,2;
左视图有两列,每列的方块数分别是:2,1;
俯视图有三列,每列的方块数分别是:1,2,2;
因此总个数为1+2+2=5个.
故答案为5
【点睛】考查了由三视图判断几何体,根据“俯视图打地基,结合正视图、左视图判断每一列的高”很容易就知道小正方体的个数.
7.C
【分析】根据俯视图与左视图的概念依次判断即可.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【详解】解:A、俯视图是带圆心的圆,左视图是等腰三角形,故本选项不合题意;
B、俯视图是圆,左视图是矩形,故本选项不合题意;
C、俯视图与左视图都是正方形,故本选项符合题意;
D、俯视图是三角形,左视图是矩形,故本选项不合题意.
故选:C.
【点睛】本题考查了几何体的三种视图,掌握定义是关键.
8.C
【分析】俯视图是指从上往下看所得到的图形,根据俯视图的定义分析解答即可.
【详解】解:这个立体图形的俯视图是一个正方形,正方形中间有一条纵向的实线.
故选:C.
【点睛】本题主要考查了立体图形的三视图,解答此题的关键是理解并掌握三视图的定义.
9.A
【分析】根据从上面看到的图形即可得到答案.
【详解】从上面看是一个正六边形,中间是一个圆,
故选:A.
【点睛】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线.
10.A
【分析】根据轴对称的性质解题即可.
【详解】根据图中所示,镜面对称后,应该为第一个图象.
故选A.
【点睛】本题考查轴对称的性质.属于简单题型.
11.B
【分析】根据主视图的定义判断即可.
【详解】解:这个几何体的主视图为:
故选B.
【点睛】本题考查三视图判断几何体,解题的关键是理解三视图的定义.
12.C
【分析】找到从左边看所得到的图形即可,注意所有看得到的棱用实线表示,看不到的部分用虚线表示
【详解】解:从左边看到的图形是:
故选C
【点睛】本题考查了简单组合体的三视图,理解看不到的且存在的是虚线解题的关键.
13.C
【分析】根据几何体的三视图可直接进行排除选项.
【详解】解:由题意得该几何体的主视图为;
故选C.
【点睛】本题主要考查三视图,熟练掌握三视图是解题的关键.
14.A
【分析】根据题意可得这个几何体的三视图为长方形和正方形,即可求解.
【详解】解:根据题意得:该几何体的三视图为长方形和正方形,
∴该几何体是长方体.
故选:A
【点睛】本题考查由三视图确定几何体的名称,熟记常见几何体的三视图的特征是解题的关键.
15.B
【分析】根据三视图可知正视图是一个正五边形,左视图是一个大长方形,里面有两个小长方形,俯视图是一个大长方形,竖着分成两个小长方形且有两条线看不见,由此即可得到答案.
【详解】解:由三视图可知正视图是一个正五边形,左视图是一个大长方形,里面有两个小长方形,俯视图是一个大长方形,竖着分成两个小长方形且有两条线看不见,由此可知这个几何体是五棱柱,
故选B.
【点睛】本题主要考查了由三视图还原几何体,解题的关键在于能够正确理解图中的三视图.
16.D
【分析】细心观察图中几何体摆放的位置,根据从左面看到的图形判定则可.
【详解】解:从左面看,共有2列,左列是1个正方形,右列是2个正方形.
故选:D.
【点睛】本题考查了从不同方向看几何体,解决本题的关键是得到从左面看得到每列正方形的具体的数目.
17.D
【分析】根据三视图的定义逐项判断即可.
【详解】解:A、B、C的俯视图都和题干中给出的图形不符,故不符合题意,
故选:D.
【点睛】此题考查由三视图判断几何体,熟知三视图的定义是解题的关键.
18.见解析
【分析】主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图.
【详解】如图所示:主视图
左视图
俯视图
【点睛】本题考查简单组合体的三视图,掌握三视图的画法是正确判断的前提,画三视图时应注意“长对正,宽相等、高平齐”.
19.(1)作图见解析
(2)6
【分析】(1)根据三视图的定义画出图形即可;
(2)根据题意,可以去了俯视图中,画箭头的小正方形.
(1)
从正面,从左面看到的形状图,如图所示:
(2)
如图,可以最多可以拿了:2+1+2+1=6(个).
故答案为:6.
【点睛】本题考查作图-三视图,简单的几何体,解题的关键是连接三视图的定义,灵活运用所学知识解决问题.
20.-2
【分析】根据相对的两个面的两个数字之和相等列出等式,进一步得到a-c,b-c的值,整体代入求值即可.
【详解】解:因为相对的两个面的两个数字之和相等,
所以,
所以,,
所以.
【点睛】本题考查了灵活运用正方体的相对面解答问题,解题的关键是得到a-c,b-c的值后用这些式子表示出原式.
21.(1)见解析;(2)6.
【分析】(1)由题意根据简单组合体三视图的画法画出相应的图形即可;
(2)根据题意在俯视图上相应位置备注出相应摆放的数目即可.
【详解】解:(1)该几何体的主视图、左视图和俯视图如下:
(2)在备注数字的位置加摆相应数量的小正方体,
所以最多可以添加6块小正方体.
故答案为:6.
【点睛】本题考查简单组合体的三视图,理解视图的意义是正确解答的前提.注意掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:_____________
一、填空题
1.一个几何体从正面看,左面看,上面看到的平面图形一样,那么这个几何体可能是________或________.
2.投影可分为________ 和________ ;一个立体图形,共有________ 种视图.
3.如图是一个立体图形的三视图,请你根据视图,说出对应的立体图形的名称:________.
4.怎样由物体的三视图想象出原物体的形状?
由三视图想象立体图形时,先分别根据____图、____图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
5.长方体、球体、三棱柱、圆柱体,这四个几何体中有三个视图都是同一种几何图形,则这一个几何体是________.
6.如图,是几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是_____.
二、单选题
7.在如图所示的几何体中,俯视图和左视图相同的是( )
A. B. C. D.
8.如图所示,是一个由正方体和正三棱柱组成的几何体,则其俯视图是( )
A. B. C. D.
9.如图所示的六角螺栓,其俯视图是( )
A. B.
C. D.
10.一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是( )
A. B. C. D.
11.从正面看如图所示的正三棱柱,得到的平面图形是( )
A. B.
C. D.
12.如图所示的几何体的左视图为( )
A. B. C. D.
13.八个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
14.如图是一个立体图形的三视图,该立体图形是( )
A.长方体 B.正方体 C.三棱柱 D.圆柱
15.如图是某几何体的三视图,该几何体是( )
A.圆柱 B.五棱柱 C.长方体 D.五棱锥
16.如图中几何体从左面看能得到( )
A. B. C. D.
17.如图是一个几何体的三种视图,则该几何体可能是( )
A. B. C. D.
三、解答题
18.画出下列几何体的主视图、左视图与俯视图.
19.一个几何体由大小相同的立方块搭成,俯视图如图所示,其中小正方形中的数字表示在该位置的立方块个数.
(1)在所给的方框中分别画出该几何体从正面,从左面看到的形状图;
(2)若允许从该几何体中拿掉部分立方块,使剩下的几何体的主视图不变,则最多可拿掉_______个立方块.
20.如图所示的是一个正方体的展开图,它的每一个面上都写有一个自然数,并且相对的两个面的两个数字之和相等,求的值.
21.如图是由一些棱长都为的小正方体组合成的简单几何体.
(1)画出该几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加__________块小正方体.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 正方体 球
【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可.
【详解】正方体从正面看,左面看,上面看到的平面图形为全等的正方形;
球从正面看,左面看,上面看到的平面图形为全等的圆,
∴这个几何体可能是正方体或球.
【点睛】考查三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.
2. 平行投影 中心投影 三
【分析】根据投影的分类:平行投影与中心投影直接填写;根据立体图形三视图的概念直接填写即可.
【详解】投影可分为平行投影和中心投影;一个立体图形,共有三种视图.
【点睛】本题考查投影的分类及立体图形的三视图,属于最基础知识,牢记相关概念是解决问题的关键.
3.四棱锥
【分析】主视图、左视图、俯视图是分别别从物体正面、左面和上面看,所得到的图形,根据给出的三视图,分析判定出即可
【详解】根据题意,
从俯视图中知,这个立体图形有4条棱,底面为正方
形,而且主、左视图中三角形的面积相等,
因此,符合条件的几何体是四棱锥.
故答案为:四棱锥.
【点睛】此题考查由三视图判断几何体,难度不大
4. 主视 俯视
【解析】略
5.球体
【分析】视图是同一种几何图形的几何体是正方体或者球体,看本题所给选项中有哪种几何体即可.
【详解】视图是同一种几何图形的几何体是正方体或者球体,所给选项中有球体,
故答案为球体.
【点睛】考查三视图的知识;掌握常见几何体的三视图知识是解决本题的关键.
6.5
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】解:由主视图与左视图可以在俯视图上标注数字为:
主视图有三列,每列的方块数分别是:1,2,2;
左视图有两列,每列的方块数分别是:2,1;
俯视图有三列,每列的方块数分别是:1,2,2;
因此总个数为1+2+2=5个.
故答案为5
【点睛】考查了由三视图判断几何体,根据“俯视图打地基,结合正视图、左视图判断每一列的高”很容易就知道小正方体的个数.
7.C
【分析】根据俯视图与左视图的概念依次判断即可.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【详解】解:A、俯视图是带圆心的圆,左视图是等腰三角形,故本选项不合题意;
B、俯视图是圆,左视图是矩形,故本选项不合题意;
C、俯视图与左视图都是正方形,故本选项符合题意;
D、俯视图是三角形,左视图是矩形,故本选项不合题意.
故选:C.
【点睛】本题考查了几何体的三种视图,掌握定义是关键.
8.C
【分析】俯视图是指从上往下看所得到的图形,根据俯视图的定义分析解答即可.
【详解】解:这个立体图形的俯视图是一个正方形,正方形中间有一条纵向的实线.
故选:C.
【点睛】本题主要考查了立体图形的三视图,解答此题的关键是理解并掌握三视图的定义.
9.A
【分析】根据从上面看到的图形即可得到答案.
【详解】从上面看是一个正六边形,中间是一个圆,
故选:A.
【点睛】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线.
10.A
【分析】根据轴对称的性质解题即可.
【详解】根据图中所示,镜面对称后,应该为第一个图象.
故选A.
【点睛】本题考查轴对称的性质.属于简单题型.
11.B
【分析】根据主视图的定义判断即可.
【详解】解:这个几何体的主视图为:
故选B.
【点睛】本题考查三视图判断几何体,解题的关键是理解三视图的定义.
12.C
【分析】找到从左边看所得到的图形即可,注意所有看得到的棱用实线表示,看不到的部分用虚线表示
【详解】解:从左边看到的图形是:
故选C
【点睛】本题考查了简单组合体的三视图,理解看不到的且存在的是虚线解题的关键.
13.C
【分析】根据几何体的三视图可直接进行排除选项.
【详解】解:由题意得该几何体的主视图为;
故选C.
【点睛】本题主要考查三视图,熟练掌握三视图是解题的关键.
14.A
【分析】根据题意可得这个几何体的三视图为长方形和正方形,即可求解.
【详解】解:根据题意得:该几何体的三视图为长方形和正方形,
∴该几何体是长方体.
故选:A
【点睛】本题考查由三视图确定几何体的名称,熟记常见几何体的三视图的特征是解题的关键.
15.B
【分析】根据三视图可知正视图是一个正五边形,左视图是一个大长方形,里面有两个小长方形,俯视图是一个大长方形,竖着分成两个小长方形且有两条线看不见,由此即可得到答案.
【详解】解:由三视图可知正视图是一个正五边形,左视图是一个大长方形,里面有两个小长方形,俯视图是一个大长方形,竖着分成两个小长方形且有两条线看不见,由此可知这个几何体是五棱柱,
故选B.
【点睛】本题主要考查了由三视图还原几何体,解题的关键在于能够正确理解图中的三视图.
16.D
【分析】细心观察图中几何体摆放的位置,根据从左面看到的图形判定则可.
【详解】解:从左面看,共有2列,左列是1个正方形,右列是2个正方形.
故选:D.
【点睛】本题考查了从不同方向看几何体,解决本题的关键是得到从左面看得到每列正方形的具体的数目.
17.D
【分析】根据三视图的定义逐项判断即可.
【详解】解:A、B、C的俯视图都和题干中给出的图形不符,故不符合题意,
故选:D.
【点睛】此题考查由三视图判断几何体,熟知三视图的定义是解题的关键.
18.见解析
【分析】主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图.
【详解】如图所示:主视图
左视图
俯视图
【点睛】本题考查简单组合体的三视图,掌握三视图的画法是正确判断的前提,画三视图时应注意“长对正,宽相等、高平齐”.
19.(1)作图见解析
(2)6
【分析】(1)根据三视图的定义画出图形即可;
(2)根据题意,可以去了俯视图中,画箭头的小正方形.
(1)
从正面,从左面看到的形状图,如图所示:
(2)
如图,可以最多可以拿了:2+1+2+1=6(个).
故答案为:6.
【点睛】本题考查作图-三视图,简单的几何体,解题的关键是连接三视图的定义,灵活运用所学知识解决问题.
20.-2
【分析】根据相对的两个面的两个数字之和相等列出等式,进一步得到a-c,b-c的值,整体代入求值即可.
【详解】解:因为相对的两个面的两个数字之和相等,
所以,
所以,,
所以.
【点睛】本题考查了灵活运用正方体的相对面解答问题,解题的关键是得到a-c,b-c的值后用这些式子表示出原式.
21.(1)见解析;(2)6.
【分析】(1)由题意根据简单组合体三视图的画法画出相应的图形即可;
(2)根据题意在俯视图上相应位置备注出相应摆放的数目即可.
【详解】解:(1)该几何体的主视图、左视图和俯视图如下:
(2)在备注数字的位置加摆相应数量的小正方体,
所以最多可以添加6块小正方体.
故答案为:6.
【点睛】本题考查简单组合体的三视图,理解视图的意义是正确解答的前提.注意掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
答案第1页,共2页
答案第1页,共2页
