2022-2023学年人教版九年级下册28.2解直角三角形及其应用练习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级下册28.2解直角三角形及其应用练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版九年级下册
解直角三角形及其应用练习题
学校:___________姓名:___________班级:________________
一、单选题
1.图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F,若BC=4,sin∠CEF=,则△AEF的面积为( )
A.3 B.4 C.5 D.6
2.小丽在小华北偏东40°的方向,则小华在小丽的( )
A.南偏西50° B.北偏西50° C.南偏西40° D.北偏西40°
3.如图,小明在距离地面米的处测得处的俯角为,处的心角为,若斜面坡度为,则斜面的长是( )米.
A. B. C. D.
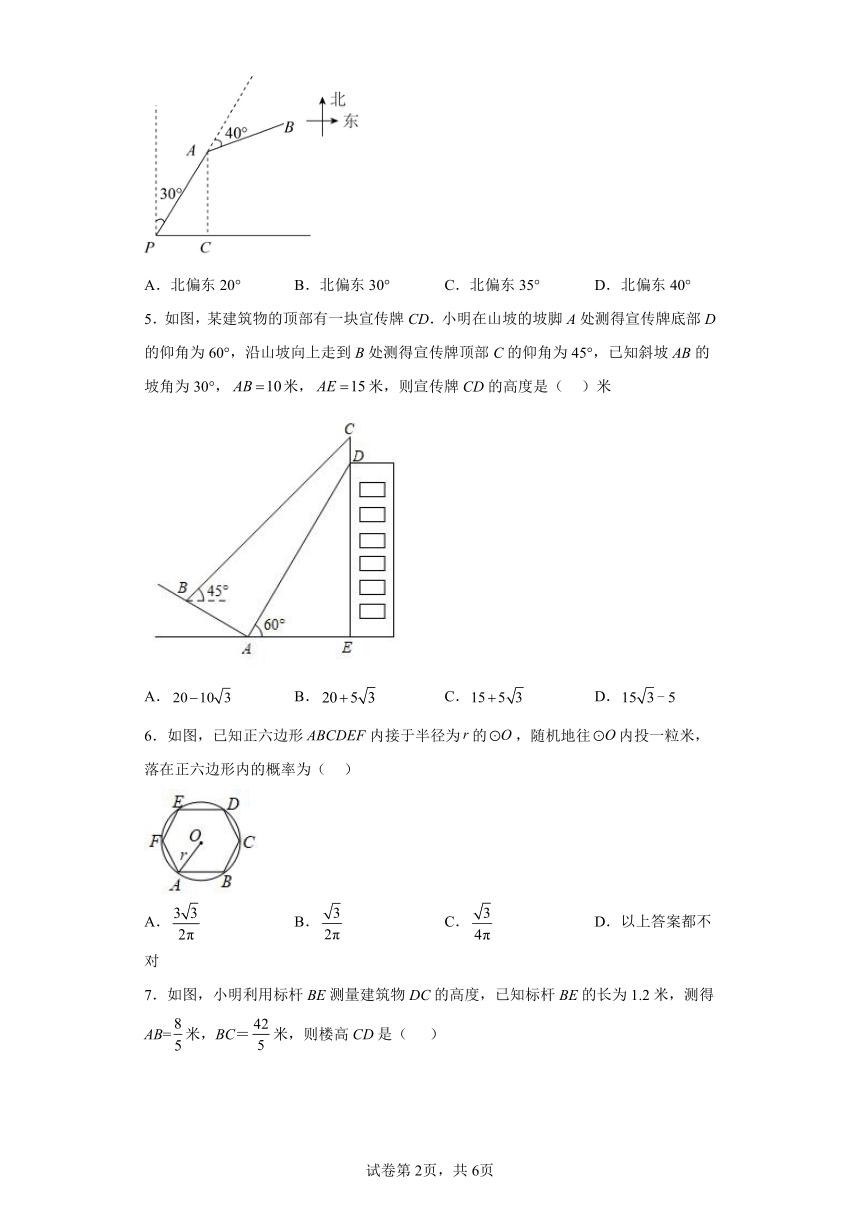
4.如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处.然后右转40°再航行到B处,在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是( )
A.北偏东20° B.北偏东30° C.北偏东35° D.北偏东40°
5.如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米
A. B. C. D.
6.如图,已知正六边形内接于半径为的,随机地往内投一粒米,落在正六边形内的概率为( )
A. B. C. D.以上答案都不对
7.如图,小明利用标杆BE测量建筑物DC的高度,已知标杆BE的长为1.2米,测得AB=米,BC=米,则楼高CD是( )
A.6.3米 B.7.5米 C.8米 D.6
8.如图,点E是 ABCD的边AB上一点,过点E作EFBC,交CD于F,点P为EF上一点,连接PB、PD.下列说法不正确的是( )
A.若∠ABP=∠CDP,则点P在 ABCD的对角线BD上
B.若AE:EB=2:3,EP:PF=1:2,则S△BEP:S△DFP=3:4
C.若S△BEP=S△DFP,则点P在AC上
D.若点P在BD上,则S△BEP=S△DFP
9.如图,一棵大树被台风拦腰刮断,树根A到刮断点的距离是4米,折断部分与地面成的夹角,那么原来这棵树的高度是( )
A.米 B.米 C.米 D.米
10.如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
二、填空题
11.在中,,有一个锐角为,,若点在直线上(不与点,重合),且,则的长为_______.
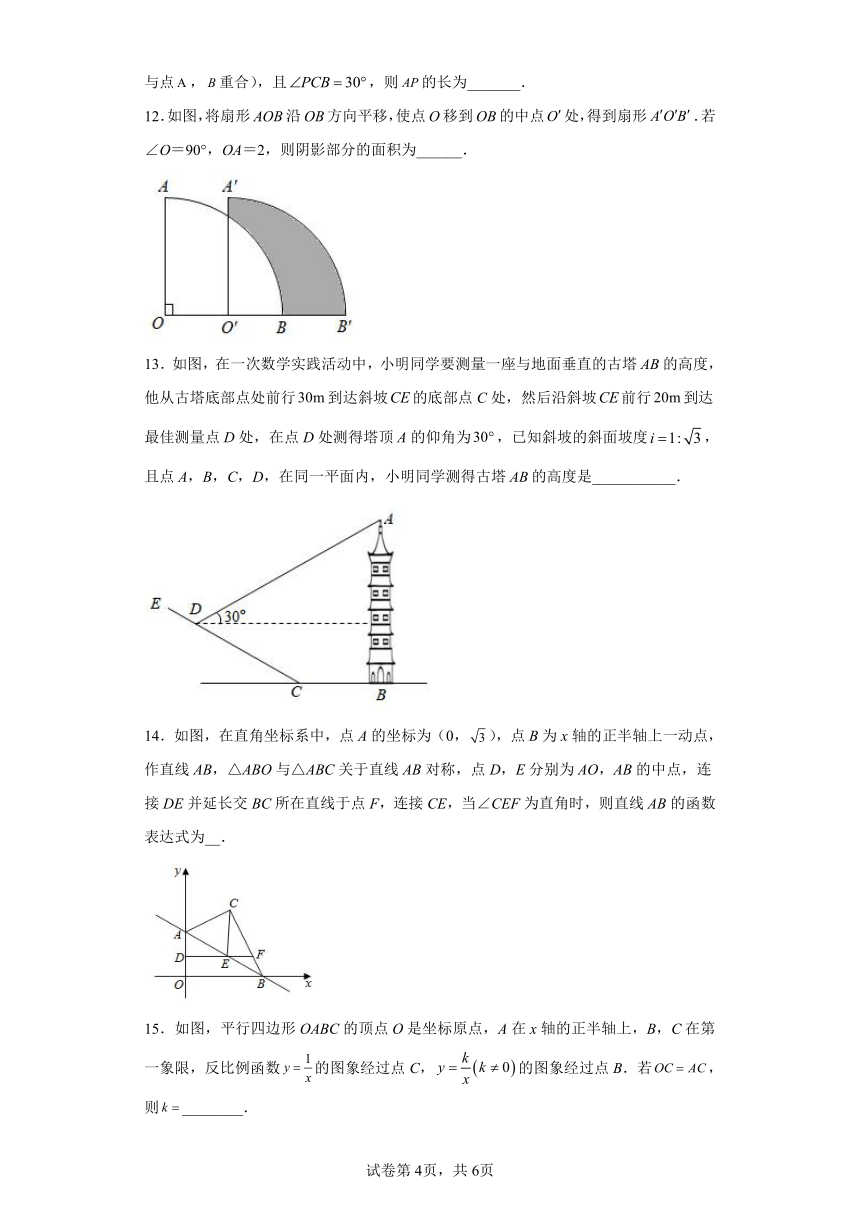
12.如图,将扇形AOB沿OB方向平移,使点O移到OB的中点处,得到扇形.若∠O=90°,OA=2,则阴影部分的面积为______.
13.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为,已知斜坡的斜面坡度,且点A,B,C,D,在同一平面内,小明同学测得古塔的高度是___________.
14.如图,在直角坐标系中,点A的坐标为(0,),点B为x轴的正半轴上一动点,作直线AB,△ABO与△ABC关于直线AB对称,点D,E分别为AO,AB的中点,连接DE并延长交BC所在直线于点F,连接CE,当∠CEF为直角时,则直线AB的函数表达式为__.
15.如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若,则________.
16.在△ABC中,,,,则______________.
17.如图,大坝横截面的迎水坡AB的坡比为1:2,(即BC:AC=1:2),若坡面AB的水平宽度AC为12米,则斜坡AB的长为________米.
18.如图,等边中,,则以线段为边构成的三角形的各角的度数分别为______________________________.
三、解答题
19.实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线的距离皆为.王诗嬑观测到高度矮圆柱的影子落在地面上,其长为;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线互相垂直,并视太阳光为平行光,测得斜坡坡度,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)若王诗嬑的身高为,且此刻她的影子完全落在地面上,则影子长为多少?
(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?
(3)若同一时间量得高圆柱落在坡面上的影子长为,则高圆柱的高度为多少?
20.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.75
21.如图是某水库大坝的横截面,坝高,背水坡BC的坡度为.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为,求背水坡新起点A与原起点B之间的距离.(参考数据:,.结果精确到0.1m)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】连接,由已知得到,再得出与的关系,由三角函数关系求得CF、BF的值,通过,用三角形面积公式计算即可.
【详解】解:连接,
∵是斜边上的中线,
∵(直角三角形斜边上的中线等于斜边的一半),
∴,
又∵,
在△ABC中,,
在△AEC中,,
∴,
,
,设,
则,即,
解得(负值舍掉),
,
∴是的垂直平分线, ∴,
,
,
故选:C.
【点睛】本题综合考查了垂直平分线的性质、直角三角形和等腰三角形的性质、勾股定理及三角函数等相关知识,熟练利用相关定理和性质进行计算是解决本题的关键.
2.C
【分析】画出示意图,确定好小丽和小华的的方向和位置即可.
【详解】解:如图所示,当小丽在小华北偏东40°的方向时,则小华在小丽的南偏西40°的方向.
故选:C
【点睛】本题考查了方位角的知识点,确定好物体的方向和位置是解题的关键.
3.B
【分析】过点作于点,根据三角函数的定义得到,根据已知条件得到,求得,解直角三角形即可得到结论.
【详解】如图所示:过点作于点,
斜面坡度为,
,
在处进行观测,测得山坡上处的俯角为,山脚处的俯角为,
,
,
,
,
,
解得:,
故AB,
故选:B.
【点睛】此题主要考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡度坡角问题,正确得出是解题关键.
4.C
【分析】连接BC,由锐角三角函数定义得AC=PA= km,则AC=AB,再由等腰三角形的性质得∠ACB=∠ABC=35°,即可得出结论.
【详解】解:如图,连接BC,
由题意得:∠ACP=∠ACD=90°,∠PAC=30°,PA=10km,∠BAE=40°,AB=km,
∴∠BAC=180°—∠PAC—∠BAE=180°—30°—40°=110°,
∵cos∠PAC==cos30°= ,
∴AC=PA=×10= km,
∴AC=AB,
∴∠ACB=∠ABC=×(180°—∠BAC)=×(180°—110°)=35°,
即B处在C处的北偏东35°方向,
故选:C.
【点睛】本题考查了解直角三角形的应用—方向角问题,等腰三角形的性质,锐角三角函数定义等知识,由锐角三角函数定义求出AC的长是解题的关键.
5.A
【分析】过点B分别作AE、DE的垂线,垂足分别为G、F,在Rt△ABG中,由已知可求得BG、AG的长,从而可易得EF及EG、BF的长度,由等腰直角三角形的性质可得CF的长度,在Rt△DAE中,由正切函数关系可求得DE的长度,从而可求得CD的长度.
【详解】过点B分别作AE、DE的垂线,垂足分别为G、F,如图
在Rt△ABG中,∠BAG=30゜
∴米,(米)
∴米
∵BG⊥AE,BF⊥ED,AE⊥ED
∴四边形BGEF是矩形
∴EF=BG=5米,米
∵∠CBF=45゜,BF⊥ED
∴∠BCF=∠CBF=45゜
∴米
在Rt△DAE中,∠DAE=60゜,AE=15米
∴(米)
∴米
故选:A
【点睛】本题考查了解直角三角形的实际应用,理解坡角、仰角的含义,构造辅助线得到直角三角形是解题的关键.
6.A
【分析】连接OB,过点O作OH⊥AB于点H,由正六边形的特点可证得△OAB是等边三角形,由特殊角的三角函数值可求出OH的长,利用三角形的面积公式即可求出△OAB的面积,进而可得出正六边形ABCDEF的面积,即可得出结果.
【详解】解:如图:连接OB,过点O作OH⊥AB于点H,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB=r,
∴△OAB是等边三角形,
∴AB=OA=OB=r,∠OAB=60°,
在中,,
∴,
∴正六边形的面积,
∵⊙O的面积=πr2,
∴米粒落在正六边形内的概率为:,
故选:A.
【点睛】本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、解直角三角形;熟练掌握正六边形的性质,通过作辅助线求出△OAB的面积是解决问题的关键.
7.B
【分析】先判断出△ABE∽△ACD,再根据相似三角形对应边成比例解答.
【详解】∵AB=,BC=
∴AC=AB+BC=10
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴AB:AC=BE:CD,
∴:10=1.2:CD,
∴CD=7.5米.
故选:B.
【点睛】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出建筑物的高度,体现了方程的思想.
8.D
【分析】根据平行四边形的性质和判定进行判断即可.
【详解】解:A、若∠ABP=∠CDP,则点P在 ABCD的对角线BD上,说法正确;
B、若AE:EB=2:3,EP:PF=1:2,则S△BEP:S△DFP=3:4,说法正确;
C、过点P作,分别交AD,BC于G,H,
∵,,
∴四边形ABHG是平行四边形,
同理:四边形CDGH、四边形BHPE,四边形DGPE都是平行四边形,
∴,,
又,
∴,
∴,
同理:,
∴点P在AC上,C说法正确;
D、若点P在BD上,不能得出EP=PF,所以S△BEP不一定等于S△DFP,说法错误;
故选:D.
【点睛】此题考查平行四边形的判定和性质,掌握平行四边形的性质是解题的关键.
9.B
【分析】通过解直角三角形即可求得.
【详解】解:在中,,
故原来这棵树的高度为:(米),
故选:B.
【点睛】本题考查了解直角三角形的应用,熟练掌握和运用解直角三角形的方法是解决本题的关键.
10.D
【分析】过点D作DE⊥BC于点E,设AB=AC=x,则AD=x-2,根据等腰Rt△ABC中,,得到∠C=45°,根据BD为△ABC的角平分线,∠A=90°,DE⊥BC,推出DE=AD=x-2,运用∠C的正弦即可求得.
【详解】解:过点D作DE⊥BC于点E,则∠DEB=∠DEC=90°,
设AB=AC=x,则AD=x-2,
∵等腰Rt△ABC中,,∠A=90°,AB=AC,,
∴∠C=(180°-∠A)=45°,
∵BD为△ABC的角平分线,
∴DE=AD=x-2,
∵,
∴,
∴,即.
故选D.
【点睛】本题主要考查了等腰直角三角形,角平分线,解直角三角形,熟练掌握等腰直角三角形的性质,角平分线的性质,正弦的定义和45°的正弦值,是解决问题的关键.
11.或9或3
【分析】分∠ABC=60、∠ABC=30°两种情况,利用数形结合的方法,分别求解即可.
【详解】解:当∠ABC=60°时,则∠BAC=30°,
∴,
∴,
当点P在线段AB上时,如图,
∵,
∴∠BPC=90°,即PC⊥AB,
∴;
当点P在AB的延长线上时,
∵,∠PBC=∠PCB+∠CPB,
∴∠CPB=30°,
∴∠CPB=∠PCB,
∴PB=BC=3,
∴AP=AB+PB=9;
当∠ABC=30°时,则∠BAC=60°,如图,
∴,
∵,
∴∠APC=60°,
∴∠ACP=60°,
∴∠APC=∠PAC=∠ACP,
∴△APC为等边三角形,
∴PA=AC=3.
综上所述,的长为或9或3.
故答案为:或9或3
【点睛】本题是解直角三角形综合题,主要考查了含30度角的直角三角形、解直角三角形,等边三角形的判定和性质等,分类求解是本题解题的关键.
12.
【分析】设与扇形交于点,连接,解,求得,根据阴影部分的面积为,即可求解.
【详解】如图,设与扇形交于点,连接,如图
是OB的中点
, OA=2,
=90°,将扇形AOB沿OB方向平移,
阴影部分的面积为
故答案为:
【点睛】本题考查了解直角三角形,求扇形面积,平移的性质,求得是解题的关键.
13.
【分析】过D作DF⊥BC于F,DH⊥AB于H,设DF=x m,CF=x m,求出x=10,则BH=DF=+30,CF=m,DH=BF,再求出AH=,即可求解.
【详解】
解:过D作DF⊥BC于F,DH⊥AB于H,
∴DH=BF,BH=DF,
∵斜坡的斜面坡度i=1:,
∴,
设DF=x m,CF=x m,
∴CD=,
∴x=10,
∴BH=DF=10m,CF=m,
∴DH=BF=+30(m),
∵∠ADH=30°,
∴AH=(m),
∴AB=AH+BH=(m),
故答案为:.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.
14.y=﹣x+
【分析】证明△ABO≌△ABC,于是可知∠CBA=∠ABO=30°,得出OB=3即可求出直线AB的函数表达式.
【详解】解:∵△ABO与△ABC关于直线AB对称,
∴∠ACB=∠AOB=90°,
∵点E是AB的中点,
∴CE=BE=EA
∴∠EAC=∠ECA,
∵∠ECA+∠ECF=90°,∠ECF+∠CFE=90°
∴∠CFE=∠BAC,
而点D,E分别为AO,AB的中点,
∴DFOB,
∴∠CFE=∠CBO=2∠CBA=2∠ABO,
∵△ABO与△ABC关于直线AB对称,
∴△ABO≌△ABC,
∴∠OAB=∠CAB=2∠ABO,
∴∠ABO=30°,
而点A的坐标为(0,),即OA=,
∴OB=3即点B的坐标为(3,0),
于是可设直线AB的函数表达式为y=kx+b,代入A、B两点坐标得
解得k=﹣,b=,
故答案为y=﹣x+.
【点睛】本题考查的是三角形的全等,并考查了用待定系数法求函数解析式,找到两个已知点的坐标是解决本题的关键.
15.3
【分析】过点C作CD⊥OA于D,过点B作BE⊥x轴于E,先证四边形CDEB为矩形,得出CD=BE,再证Rt△COD≌Rt△BAE(HL),根据S平行四边形OCBA=4S△OCD=2,再求S△OBA=即可.
【详解】解:过点C作CD⊥OA于D,过点B作BE⊥x轴于E,
∴CD∥BE,
∵四边形ABCO为平行四边形,
∴ ,即,OC=AB,
∴四边形CDEB为平行四边形,
∵CD⊥OA,
∴四边形CDEB为矩形,
∴CD=BE,
∴在Rt△COD和Rt△BAE中,
,
∴Rt△COD≌Rt△BAE(HL),
∴S△OCD=S△ABE,
∵OC=AC,CD⊥OA,
∴OD=AD,
∵反比例函数的图象经过点C,
∴S△OCD=S△CAD=,
∴S平行四边形OCBA=4S△OCD=2,
∴S△OBA=,
∴S△OBE=S△OBA+S△ABE=,
∴.
故答案为3.
【点睛】本题考查反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质,掌握反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质.
16.或
【分析】画出图形,分△ABC为锐角三角形和钝角三角形两种情况讨论即可.
【详解】解:情况一:当△ABC为锐角三角形时,如图1所示:
过A点作AH⊥BC于H,
∵∠B=45°,
∴△ABH为等腰直角三角形,
∴,
在Rt△ACH中,由勾股定理可知:,
∴.
情况二:当△ABC为钝角三角形时,如图2所示:
由情况一知:,,
∴.
故答案为:或.
【点睛】本题考察了等腰直角三角形的性质及勾股定理的应用,本题的关键是能将△ABC分成锐角三角形或钝角三角形分类讨论.
17.
【分析】根据坡面AB的坡比以及AC的值,求出BC,再利用勾股定理即可求出斜面AB的长.
【详解】解:∵大坝横截面的迎水坡AB的坡比为1:2,AC=12米,
∴,
∴BC=6,
∴(米)
故答案为:.
【点睛】本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,能根据坡度求出BC是解题关键.
18.,,.
【分析】通过旋转至,可得 是等边三角形,将 放在一个三角形中,进而求出各角大小。
【详解】解:将逆时针旋转,得到,
∵,是等边三角形,且旋转角相等,则,
∴是等边三角形. 则
又∵ ∴
故以线段三边构成的三角形为
所以
故答案为: .
【点睛】此题旨在考查图形旋转的特性和实际应用,以及等边三角形的性质,熟练掌握图形的旋转的应用是解题的关键.
19.(1)120cm;(2)正确;(3)280cm
【分析】(1)根据同一时刻,物长与影从成正比,构建方程即可解决问题.
(2)根据落在地面上的影子皆与坡脚水平线互相垂直,并视太阳光为平行光,结合横截面分析可得;
(3)过点F作FG⊥CE于点G,设FG=4m,CG=3m,利用勾股定理求出CG和FG,得到BG,过点F作FH⊥AB于点H,再根据同一时刻身高与影长的比例,求出AH的长度,即可得到AB.
【详解】解:(1)设王诗嬑的影长为xcm,
由题意可得:,
解得:x=120,
经检验:x=120是分式方程的解,
王诗嬑的的影子长为120cm;
(2)正确,
因为高圆柱在地面的影子与MN垂直,所以太阳光的光线与MN垂直,
则在斜坡上的影子也与MN垂直,则过斜坡上的影子的横截面与MN垂直,
而横截面与地面垂直,高圆柱也与地面垂直,
∴高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内;
(3)如图,AB为高圆柱,AF为太阳光,△CDE为斜坡,CF为圆柱在斜坡上的影子,
过点F作FG⊥CE于点G,
由题意可得:BC=100,CF=100,
∵斜坡坡度,
∴,
∴设FG=4m,CG=3m,在△CFG中,
,
解得:m=20,
∴CG=60,FG=80,
∴BG=BC+CG=160,
过点F作FH⊥AB于点H,
∵同一时刻,90cm矮圆柱的影子落在地面上,其长为72cm,
FG⊥BE,AB⊥BE,FH⊥AB,
可知四边形HBGF为矩形,
∴,
∴AH==200,
∴AB=AH+BH=AH+FG=200+80=280,
故高圆柱的高度为280cm.
【点睛】本题考查了解分式方程,解直角三角形,平行投影,矩形的判定和性质等知识,解题的关键是理解实际物体与影长之间的关系解决问题,属于中考常考题型.
20.菜园与果园之间的距离为630米
【分析】过点作,交于点,则,四边形是矩形,在中,求得,CF=240,进而求得AE=210,在中,利用正切进行求解即可.
【详解】解:如图,过点作,交于点,则,
∵∠B=90°,
四边形是矩形,
,BC=EF,
在中,,
∴BE=240,
∴AE=AB-BE=210,
在中,,,
米.
∴BC=EF=DF+DE=180+450=630
答:菜园与果园之间的距离630米.
【点睛】本题考查了解直角三角形的应用,掌握直角三角形中的边角关系是解题的关键.
21.背水坡新起点A与原起点B之间的距离约为14.6m
【分析】通过解直角三角形和,分别求出AD和BD的长,由求出AB的长.
【详解】解:在中,∵背水坡BC的坡度,
∴,
∴.
在中,∵背水坡AC的坡度,
∴,
∴,
∴.
答:背水坡新起点A与原起点B之间的距离约为14.6m.
【点睛】本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度.
答案第1页,共2页
答案第1页,共2页
解直角三角形及其应用练习题
学校:___________姓名:___________班级:________________
一、单选题
1.图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F,若BC=4,sin∠CEF=,则△AEF的面积为( )
A.3 B.4 C.5 D.6
2.小丽在小华北偏东40°的方向,则小华在小丽的( )
A.南偏西50° B.北偏西50° C.南偏西40° D.北偏西40°
3.如图,小明在距离地面米的处测得处的俯角为,处的心角为,若斜面坡度为,则斜面的长是( )米.
A. B. C. D.
4.如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处.然后右转40°再航行到B处,在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是( )
A.北偏东20° B.北偏东30° C.北偏东35° D.北偏东40°
5.如图,某建筑物的顶部有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°,已知斜坡AB的坡角为30°,米,米,则宣传牌CD的高度是( )米
A. B. C. D.
6.如图,已知正六边形内接于半径为的,随机地往内投一粒米,落在正六边形内的概率为( )
A. B. C. D.以上答案都不对
7.如图,小明利用标杆BE测量建筑物DC的高度,已知标杆BE的长为1.2米,测得AB=米,BC=米,则楼高CD是( )
A.6.3米 B.7.5米 C.8米 D.6
8.如图,点E是 ABCD的边AB上一点,过点E作EFBC,交CD于F,点P为EF上一点,连接PB、PD.下列说法不正确的是( )
A.若∠ABP=∠CDP,则点P在 ABCD的对角线BD上
B.若AE:EB=2:3,EP:PF=1:2,则S△BEP:S△DFP=3:4
C.若S△BEP=S△DFP,则点P在AC上
D.若点P在BD上,则S△BEP=S△DFP
9.如图,一棵大树被台风拦腰刮断,树根A到刮断点的距离是4米,折断部分与地面成的夹角,那么原来这棵树的高度是( )
A.米 B.米 C.米 D.米
10.如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
二、填空题
11.在中,,有一个锐角为,,若点在直线上(不与点,重合),且,则的长为_______.
12.如图,将扇形AOB沿OB方向平移,使点O移到OB的中点处,得到扇形.若∠O=90°,OA=2,则阴影部分的面积为______.
13.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔的高度,他从古塔底部点处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为,已知斜坡的斜面坡度,且点A,B,C,D,在同一平面内,小明同学测得古塔的高度是___________.
14.如图,在直角坐标系中,点A的坐标为(0,),点B为x轴的正半轴上一动点,作直线AB,△ABO与△ABC关于直线AB对称,点D,E分别为AO,AB的中点,连接DE并延长交BC所在直线于点F,连接CE,当∠CEF为直角时,则直线AB的函数表达式为__.
15.如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若,则________.
16.在△ABC中,,,,则______________.
17.如图,大坝横截面的迎水坡AB的坡比为1:2,(即BC:AC=1:2),若坡面AB的水平宽度AC为12米,则斜坡AB的长为________米.
18.如图,等边中,,则以线段为边构成的三角形的各角的度数分别为______________________________.
三、解答题
19.实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线的距离皆为.王诗嬑观测到高度矮圆柱的影子落在地面上,其长为;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线互相垂直,并视太阳光为平行光,测得斜坡坡度,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)若王诗嬑的身高为,且此刻她的影子完全落在地面上,则影子长为多少?
(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?
(3)若同一时间量得高圆柱落在坡面上的影子长为,则高圆柱的高度为多少?
20.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.75
21.如图是某水库大坝的横截面,坝高,背水坡BC的坡度为.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为,求背水坡新起点A与原起点B之间的距离.(参考数据:,.结果精确到0.1m)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】连接,由已知得到,再得出与的关系,由三角函数关系求得CF、BF的值,通过,用三角形面积公式计算即可.
【详解】解:连接,
∵是斜边上的中线,
∵(直角三角形斜边上的中线等于斜边的一半),
∴,
又∵,
在△ABC中,,
在△AEC中,,
∴,
,
,设,
则,即,
解得(负值舍掉),
,
∴是的垂直平分线, ∴,
,
,
故选:C.
【点睛】本题综合考查了垂直平分线的性质、直角三角形和等腰三角形的性质、勾股定理及三角函数等相关知识,熟练利用相关定理和性质进行计算是解决本题的关键.
2.C
【分析】画出示意图,确定好小丽和小华的的方向和位置即可.
【详解】解:如图所示,当小丽在小华北偏东40°的方向时,则小华在小丽的南偏西40°的方向.
故选:C
【点睛】本题考查了方位角的知识点,确定好物体的方向和位置是解题的关键.
3.B
【分析】过点作于点,根据三角函数的定义得到,根据已知条件得到,求得,解直角三角形即可得到结论.
【详解】如图所示:过点作于点,
斜面坡度为,
,
在处进行观测,测得山坡上处的俯角为,山脚处的俯角为,
,
,
,
,
,
解得:,
故AB,
故选:B.
【点睛】此题主要考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡度坡角问题,正确得出是解题关键.
4.C
【分析】连接BC,由锐角三角函数定义得AC=PA= km,则AC=AB,再由等腰三角形的性质得∠ACB=∠ABC=35°,即可得出结论.
【详解】解:如图,连接BC,
由题意得:∠ACP=∠ACD=90°,∠PAC=30°,PA=10km,∠BAE=40°,AB=km,
∴∠BAC=180°—∠PAC—∠BAE=180°—30°—40°=110°,
∵cos∠PAC==cos30°= ,
∴AC=PA=×10= km,
∴AC=AB,
∴∠ACB=∠ABC=×(180°—∠BAC)=×(180°—110°)=35°,
即B处在C处的北偏东35°方向,
故选:C.
【点睛】本题考查了解直角三角形的应用—方向角问题,等腰三角形的性质,锐角三角函数定义等知识,由锐角三角函数定义求出AC的长是解题的关键.
5.A
【分析】过点B分别作AE、DE的垂线,垂足分别为G、F,在Rt△ABG中,由已知可求得BG、AG的长,从而可易得EF及EG、BF的长度,由等腰直角三角形的性质可得CF的长度,在Rt△DAE中,由正切函数关系可求得DE的长度,从而可求得CD的长度.
【详解】过点B分别作AE、DE的垂线,垂足分别为G、F,如图
在Rt△ABG中,∠BAG=30゜
∴米,(米)
∴米
∵BG⊥AE,BF⊥ED,AE⊥ED
∴四边形BGEF是矩形
∴EF=BG=5米,米
∵∠CBF=45゜,BF⊥ED
∴∠BCF=∠CBF=45゜
∴米
在Rt△DAE中,∠DAE=60゜,AE=15米
∴(米)
∴米
故选:A
【点睛】本题考查了解直角三角形的实际应用,理解坡角、仰角的含义,构造辅助线得到直角三角形是解题的关键.
6.A
【分析】连接OB,过点O作OH⊥AB于点H,由正六边形的特点可证得△OAB是等边三角形,由特殊角的三角函数值可求出OH的长,利用三角形的面积公式即可求出△OAB的面积,进而可得出正六边形ABCDEF的面积,即可得出结果.
【详解】解:如图:连接OB,过点O作OH⊥AB于点H,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB=r,
∴△OAB是等边三角形,
∴AB=OA=OB=r,∠OAB=60°,
在中,,
∴,
∴正六边形的面积,
∵⊙O的面积=πr2,
∴米粒落在正六边形内的概率为:,
故选:A.
【点睛】本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、解直角三角形;熟练掌握正六边形的性质,通过作辅助线求出△OAB的面积是解决问题的关键.
7.B
【分析】先判断出△ABE∽△ACD,再根据相似三角形对应边成比例解答.
【详解】∵AB=,BC=
∴AC=AB+BC=10
∵BE⊥AC,CD⊥AC,
∴BE∥CD,
∴AB:AC=BE:CD,
∴:10=1.2:CD,
∴CD=7.5米.
故选:B.
【点睛】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出建筑物的高度,体现了方程的思想.
8.D
【分析】根据平行四边形的性质和判定进行判断即可.
【详解】解:A、若∠ABP=∠CDP,则点P在 ABCD的对角线BD上,说法正确;
B、若AE:EB=2:3,EP:PF=1:2,则S△BEP:S△DFP=3:4,说法正确;
C、过点P作,分别交AD,BC于G,H,
∵,,
∴四边形ABHG是平行四边形,
同理:四边形CDGH、四边形BHPE,四边形DGPE都是平行四边形,
∴,,
又,
∴,
∴,
同理:,
∴点P在AC上,C说法正确;
D、若点P在BD上,不能得出EP=PF,所以S△BEP不一定等于S△DFP,说法错误;
故选:D.
【点睛】此题考查平行四边形的判定和性质,掌握平行四边形的性质是解题的关键.
9.B
【分析】通过解直角三角形即可求得.
【详解】解:在中,,
故原来这棵树的高度为:(米),
故选:B.
【点睛】本题考查了解直角三角形的应用,熟练掌握和运用解直角三角形的方法是解决本题的关键.
10.D
【分析】过点D作DE⊥BC于点E,设AB=AC=x,则AD=x-2,根据等腰Rt△ABC中,,得到∠C=45°,根据BD为△ABC的角平分线,∠A=90°,DE⊥BC,推出DE=AD=x-2,运用∠C的正弦即可求得.
【详解】解:过点D作DE⊥BC于点E,则∠DEB=∠DEC=90°,
设AB=AC=x,则AD=x-2,
∵等腰Rt△ABC中,,∠A=90°,AB=AC,,
∴∠C=(180°-∠A)=45°,
∵BD为△ABC的角平分线,
∴DE=AD=x-2,
∵,
∴,
∴,即.
故选D.
【点睛】本题主要考查了等腰直角三角形,角平分线,解直角三角形,熟练掌握等腰直角三角形的性质,角平分线的性质,正弦的定义和45°的正弦值,是解决问题的关键.
11.或9或3
【分析】分∠ABC=60、∠ABC=30°两种情况,利用数形结合的方法,分别求解即可.
【详解】解:当∠ABC=60°时,则∠BAC=30°,
∴,
∴,
当点P在线段AB上时,如图,
∵,
∴∠BPC=90°,即PC⊥AB,
∴;
当点P在AB的延长线上时,
∵,∠PBC=∠PCB+∠CPB,
∴∠CPB=30°,
∴∠CPB=∠PCB,
∴PB=BC=3,
∴AP=AB+PB=9;
当∠ABC=30°时,则∠BAC=60°,如图,
∴,
∵,
∴∠APC=60°,
∴∠ACP=60°,
∴∠APC=∠PAC=∠ACP,
∴△APC为等边三角形,
∴PA=AC=3.
综上所述,的长为或9或3.
故答案为:或9或3
【点睛】本题是解直角三角形综合题,主要考查了含30度角的直角三角形、解直角三角形,等边三角形的判定和性质等,分类求解是本题解题的关键.
12.
【分析】设与扇形交于点,连接,解,求得,根据阴影部分的面积为,即可求解.
【详解】如图,设与扇形交于点,连接,如图
是OB的中点
, OA=2,
=90°,将扇形AOB沿OB方向平移,
阴影部分的面积为
故答案为:
【点睛】本题考查了解直角三角形,求扇形面积,平移的性质,求得是解题的关键.
13.
【分析】过D作DF⊥BC于F,DH⊥AB于H,设DF=x m,CF=x m,求出x=10,则BH=DF=+30,CF=m,DH=BF,再求出AH=,即可求解.
【详解】
解:过D作DF⊥BC于F,DH⊥AB于H,
∴DH=BF,BH=DF,
∵斜坡的斜面坡度i=1:,
∴,
设DF=x m,CF=x m,
∴CD=,
∴x=10,
∴BH=DF=10m,CF=m,
∴DH=BF=+30(m),
∵∠ADH=30°,
∴AH=(m),
∴AB=AH+BH=(m),
故答案为:.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.
14.y=﹣x+
【分析】证明△ABO≌△ABC,于是可知∠CBA=∠ABO=30°,得出OB=3即可求出直线AB的函数表达式.
【详解】解:∵△ABO与△ABC关于直线AB对称,
∴∠ACB=∠AOB=90°,
∵点E是AB的中点,
∴CE=BE=EA
∴∠EAC=∠ECA,
∵∠ECA+∠ECF=90°,∠ECF+∠CFE=90°
∴∠CFE=∠BAC,
而点D,E分别为AO,AB的中点,
∴DFOB,
∴∠CFE=∠CBO=2∠CBA=2∠ABO,
∵△ABO与△ABC关于直线AB对称,
∴△ABO≌△ABC,
∴∠OAB=∠CAB=2∠ABO,
∴∠ABO=30°,
而点A的坐标为(0,),即OA=,
∴OB=3即点B的坐标为(3,0),
于是可设直线AB的函数表达式为y=kx+b,代入A、B两点坐标得
解得k=﹣,b=,
故答案为y=﹣x+.
【点睛】本题考查的是三角形的全等,并考查了用待定系数法求函数解析式,找到两个已知点的坐标是解决本题的关键.
15.3
【分析】过点C作CD⊥OA于D,过点B作BE⊥x轴于E,先证四边形CDEB为矩形,得出CD=BE,再证Rt△COD≌Rt△BAE(HL),根据S平行四边形OCBA=4S△OCD=2,再求S△OBA=即可.
【详解】解:过点C作CD⊥OA于D,过点B作BE⊥x轴于E,
∴CD∥BE,
∵四边形ABCO为平行四边形,
∴ ,即,OC=AB,
∴四边形CDEB为平行四边形,
∵CD⊥OA,
∴四边形CDEB为矩形,
∴CD=BE,
∴在Rt△COD和Rt△BAE中,
,
∴Rt△COD≌Rt△BAE(HL),
∴S△OCD=S△ABE,
∵OC=AC,CD⊥OA,
∴OD=AD,
∵反比例函数的图象经过点C,
∴S△OCD=S△CAD=,
∴S平行四边形OCBA=4S△OCD=2,
∴S△OBA=,
∴S△OBE=S△OBA+S△ABE=,
∴.
故答案为3.
【点睛】本题考查反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质,掌握反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质.
16.或
【分析】画出图形,分△ABC为锐角三角形和钝角三角形两种情况讨论即可.
【详解】解:情况一:当△ABC为锐角三角形时,如图1所示:
过A点作AH⊥BC于H,
∵∠B=45°,
∴△ABH为等腰直角三角形,
∴,
在Rt△ACH中,由勾股定理可知:,
∴.
情况二:当△ABC为钝角三角形时,如图2所示:
由情况一知:,,
∴.
故答案为:或.
【点睛】本题考察了等腰直角三角形的性质及勾股定理的应用,本题的关键是能将△ABC分成锐角三角形或钝角三角形分类讨论.
17.
【分析】根据坡面AB的坡比以及AC的值,求出BC,再利用勾股定理即可求出斜面AB的长.
【详解】解:∵大坝横截面的迎水坡AB的坡比为1:2,AC=12米,
∴,
∴BC=6,
∴(米)
故答案为:.
【点睛】本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,能根据坡度求出BC是解题关键.
18.,,.
【分析】通过旋转至,可得 是等边三角形,将 放在一个三角形中,进而求出各角大小。
【详解】解:将逆时针旋转,得到,
∵,是等边三角形,且旋转角相等,则,
∴是等边三角形. 则
又∵ ∴
故以线段三边构成的三角形为
所以
故答案为: .
【点睛】此题旨在考查图形旋转的特性和实际应用,以及等边三角形的性质,熟练掌握图形的旋转的应用是解题的关键.
19.(1)120cm;(2)正确;(3)280cm
【分析】(1)根据同一时刻,物长与影从成正比,构建方程即可解决问题.
(2)根据落在地面上的影子皆与坡脚水平线互相垂直,并视太阳光为平行光,结合横截面分析可得;
(3)过点F作FG⊥CE于点G,设FG=4m,CG=3m,利用勾股定理求出CG和FG,得到BG,过点F作FH⊥AB于点H,再根据同一时刻身高与影长的比例,求出AH的长度,即可得到AB.
【详解】解:(1)设王诗嬑的影长为xcm,
由题意可得:,
解得:x=120,
经检验:x=120是分式方程的解,
王诗嬑的的影子长为120cm;
(2)正确,
因为高圆柱在地面的影子与MN垂直,所以太阳光的光线与MN垂直,
则在斜坡上的影子也与MN垂直,则过斜坡上的影子的横截面与MN垂直,
而横截面与地面垂直,高圆柱也与地面垂直,
∴高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内;
(3)如图,AB为高圆柱,AF为太阳光,△CDE为斜坡,CF为圆柱在斜坡上的影子,
过点F作FG⊥CE于点G,
由题意可得:BC=100,CF=100,
∵斜坡坡度,
∴,
∴设FG=4m,CG=3m,在△CFG中,
,
解得:m=20,
∴CG=60,FG=80,
∴BG=BC+CG=160,
过点F作FH⊥AB于点H,
∵同一时刻,90cm矮圆柱的影子落在地面上,其长为72cm,
FG⊥BE,AB⊥BE,FH⊥AB,
可知四边形HBGF为矩形,
∴,
∴AH==200,
∴AB=AH+BH=AH+FG=200+80=280,
故高圆柱的高度为280cm.
【点睛】本题考查了解分式方程,解直角三角形,平行投影,矩形的判定和性质等知识,解题的关键是理解实际物体与影长之间的关系解决问题,属于中考常考题型.
20.菜园与果园之间的距离为630米
【分析】过点作,交于点,则,四边形是矩形,在中,求得,CF=240,进而求得AE=210,在中,利用正切进行求解即可.
【详解】解:如图,过点作,交于点,则,
∵∠B=90°,
四边形是矩形,
,BC=EF,
在中,,
∴BE=240,
∴AE=AB-BE=210,
在中,,,
米.
∴BC=EF=DF+DE=180+450=630
答:菜园与果园之间的距离630米.
【点睛】本题考查了解直角三角形的应用,掌握直角三角形中的边角关系是解题的关键.
21.背水坡新起点A与原起点B之间的距离约为14.6m
【分析】通过解直角三角形和,分别求出AD和BD的长,由求出AB的长.
【详解】解:在中,∵背水坡BC的坡度,
∴,
∴.
在中,∵背水坡AC的坡度,
∴,
∴,
∴.
答:背水坡新起点A与原起点B之间的距离约为14.6m.
【点睛】本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度.
答案第1页,共2页
答案第1页,共2页
