2022-2023学年人教版九年级下 27.3 位似课时1位似图形练习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级下 27.3 位似课时1位似图形练习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 413.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览

文档简介
2022-2023学年人教版九年级下第二十七章位似
课时1位似图形练习题
学校:___________姓名:___________班级:___________
一、单选题
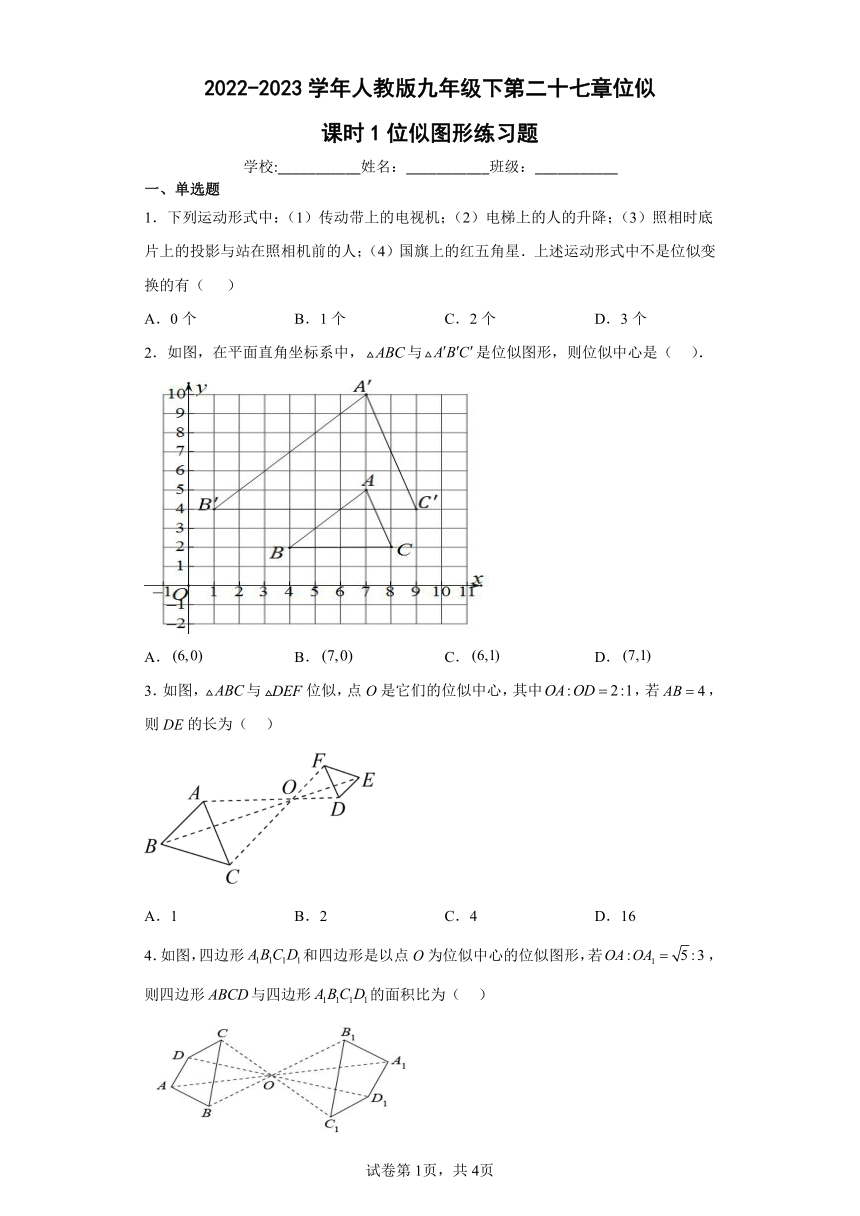
1.下列运动形式中:(1)传动带上的电视机;(2)电梯上的人的升降;(3)照相时底片上的投影与站在照相机前的人;(4)国旗上的红五角星.上述运动形式中不是位似变换的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,在平面直角坐标系中,与是位似图形,则位似中心是( ).
A. B. C. D.
3.如图,与位似,点O是它们的位似中心,其中,若,则DE的长为( )
A.1 B.2 C.4 D.16
4.如图,四边形和四边形是以点O为位似中心的位似图形,若,则四边形与四边形的面积比为( )
A. B. C. D.
5.如图,图形甲与图形乙是位似图形,是位似中心,位似比为,点,的对应点分别为点,.若,则的长为( )
A.8 B.9 C.10 D.15
6.如图,在中,,,是的中点,在上取一点,使∽,则的长是( )
A. B. C. D.
二、解答题
7.指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心.
(1) (2) (3) (4)
8.如图11×7的网格中,每个小正方形的边长均为1个单位长度,点A、B、C都在格点上(两条网格线的交点叫格点)
(1)在线段BC下方用无刻度直尺作出一点O,使得
(2)以O为位似中心,将放大为原来的2倍,得对应,请在网格中作出.
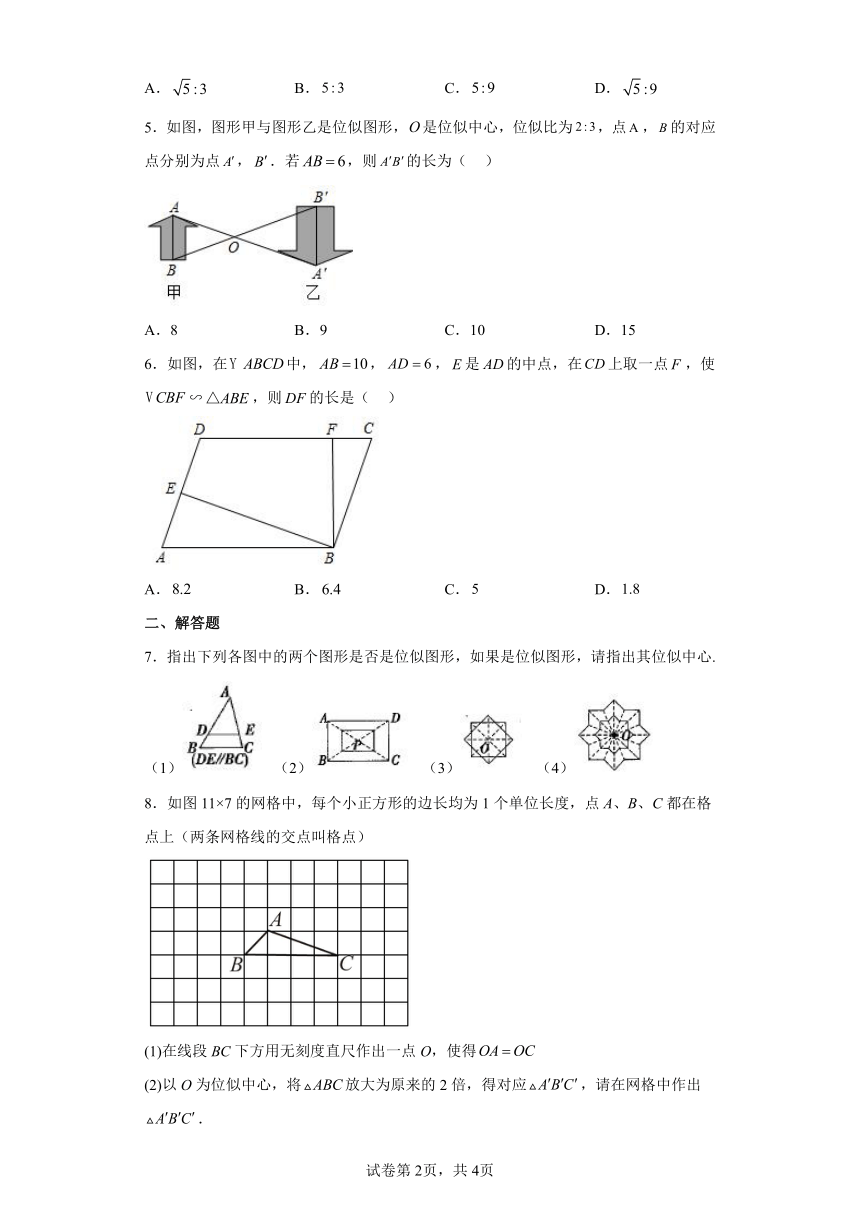
9.如图,是由5×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
(1)在图1中,画出平行四边形ABCD,并直接写出它的面积;
(2)在图2中,画出△ABC的中线AE;
(3)在图3中,在AC上找点F,连结BF,使△ABF的面积是△CBF的面积.
10.背景:一次小组合作探究课上,小明将两个正方形按如图1所示的位置摆放(点、、在同一条直线上),小组讨论后,提出了下列三个问题,请你帮助解答:
(1)如图2,将正方形绕点按逆时针方向旋转,则与的数量关系为___________,位置关系为___________.(直接写出答案)
(2)如图3,把背景中的正方形分别改写成矩形和矩形,且,,,将矩形绕点按顺时针方向旋转,求与的数量关系和位置关系;
(3)在(2)的条件下,小组发现:在旋转过程中,的值是定值,请求出这个定值.(直接写出答案)
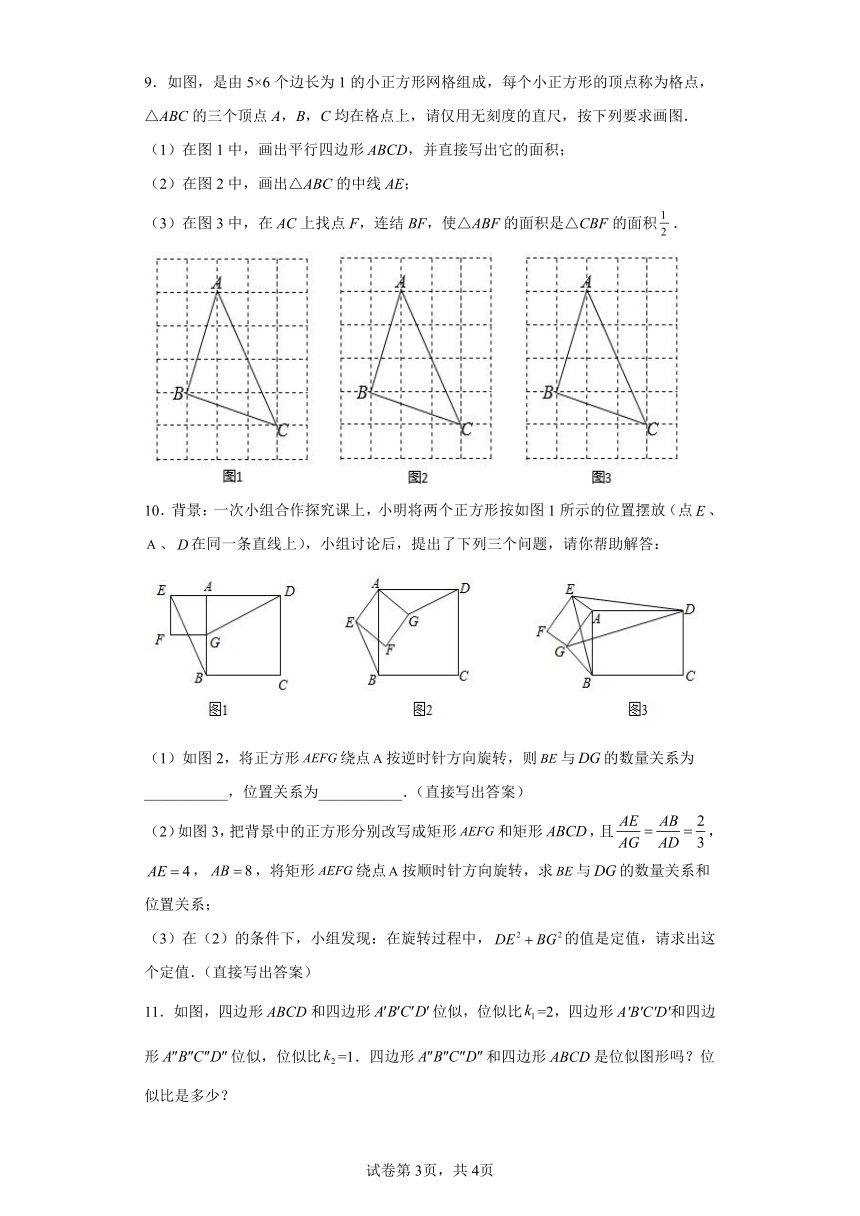
11.如图,四边形ABCD和四边形位似,位似比=2,四边形A′B′C′D′和四边形位似,位似比=1.四边形和四边形ABCD是位似图形吗?位似比是多少?
三、填空题
12.如图,△OAB与△OCD是以点O为位似中心的位似图形,点B在OD上,AE、CB分别是△OAB、△OCD的中线,则AE:CB的值为______
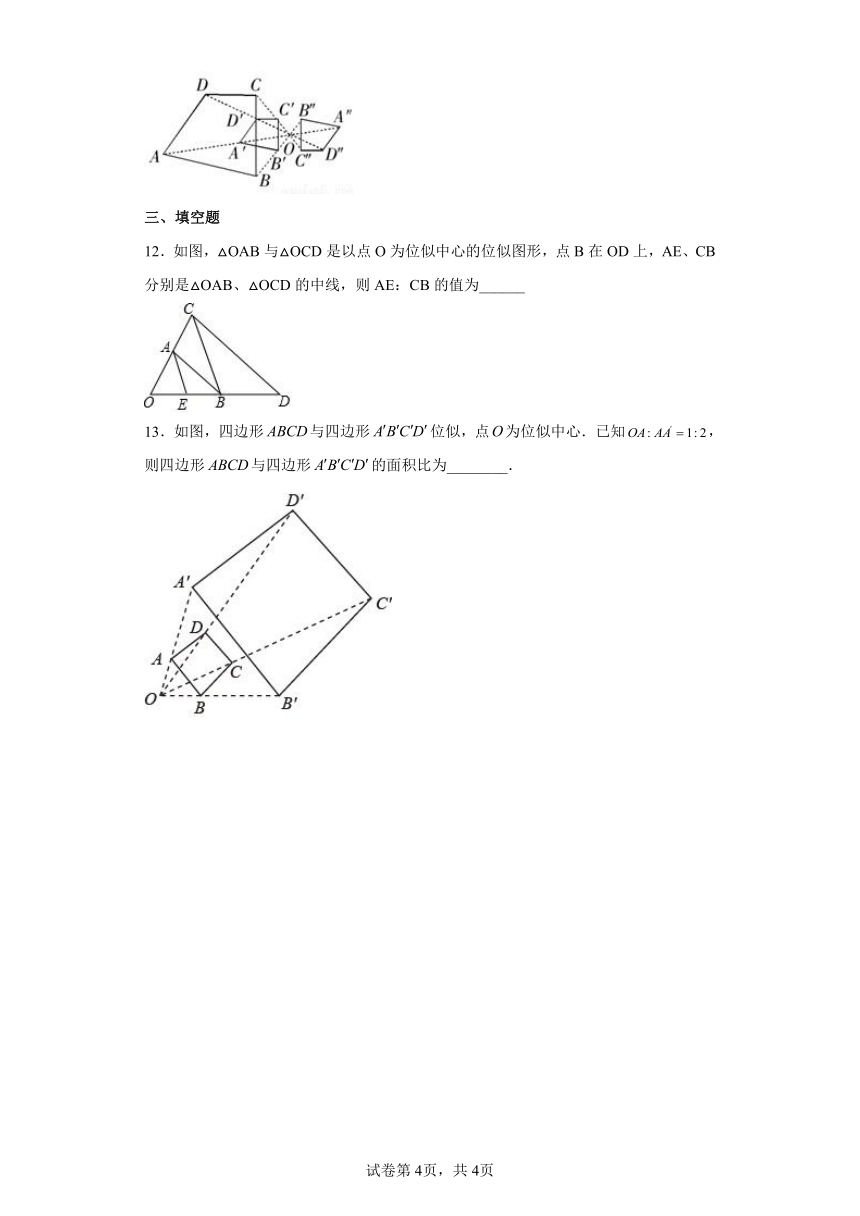
13.如图,四边形与四边形位似,点为位似中心.已知,则四边形与四边形的面积比为________.
试卷第11页,共33页
试卷第11页,共33页
参考答案
1.B
【分析】位似变换必须满足对应点的连线相交于一点,由此分析即可.
【详解】解:(1)传动带上的电视机,和(2)电梯上的人的升降;是平移变换;(4)国旗上的红五角星;它们都不满足对应点的连线相交于一点,则不是位似变换;
(3)照相时底片上的投影与站在照相机前的人;满足对应点的连线相交于一点,则它属于位似变换;
故选:B.
【点睛】本题考查位似变换的定义,掌握位似变换的要点是对应点的连线相交于一点是解题关键.
2.B
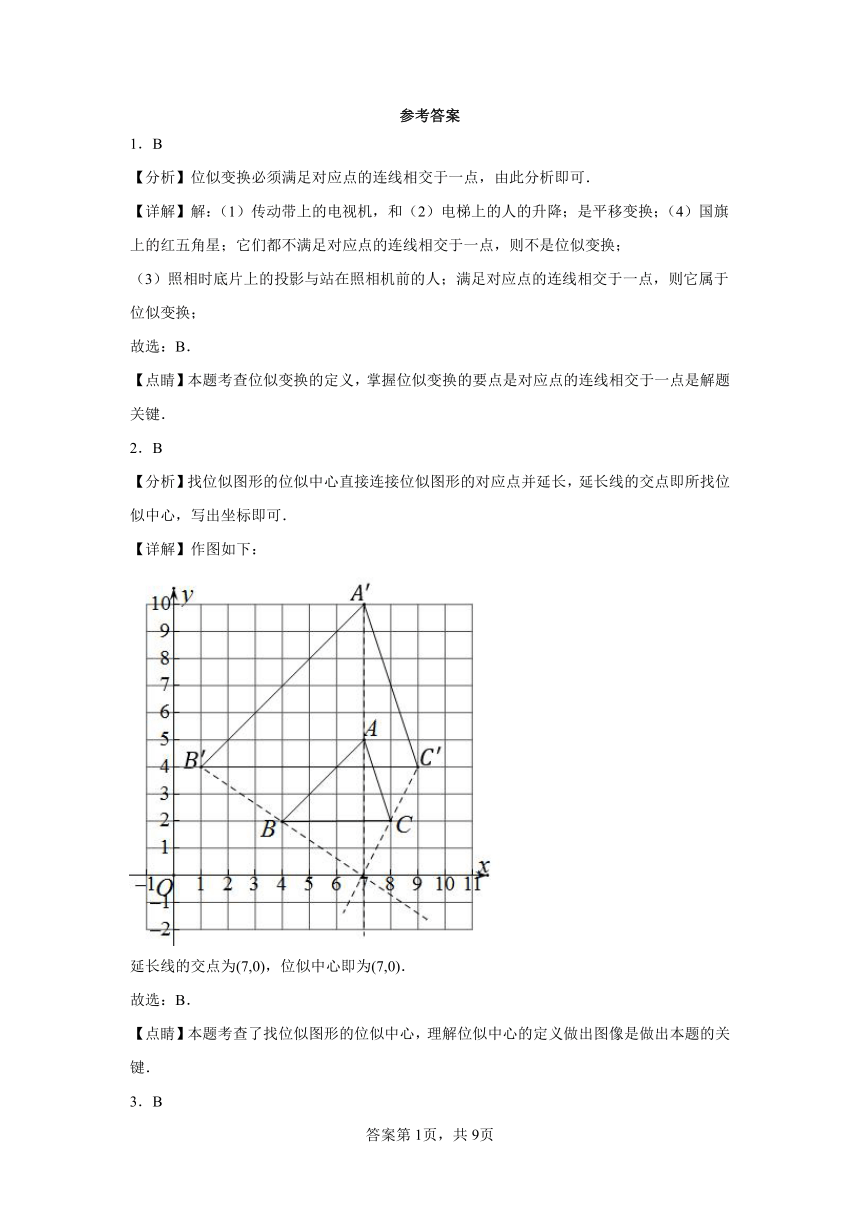
【分析】找位似图形的位似中心直接连接位似图形的对应点并延长,延长线的交点即所找位似中心,写出坐标即可.
【详解】作图如下:
延长线的交点为(7,0),位似中心即为(7,0).
故选:B.
【点睛】本题考查了找位似图形的位似中心,理解位似中心的定义做出图像是做出本题的关键.
3.B
【分析】根据位似图形的性质得出位似比,进而得出DE的长.
【详解】解:∵△ABC与△DEF位似,点O是它们的位似中心,其中OA:OD=2:1,
∴AB:DE=2:1,
∵AB=4,
∴DE的长为:2.
故选:B.
【点睛】本题考查的是位似变换,正确掌握位似图形的性质是解题关键.
4.C
【分析】根据面积比是相似比的平方直接求解即可.
【详解】解:四边形和四边形是以点为位似中心的位似图形, ,
则四边形与四边形的相似比为:,
∴四边形与四边形的面积比为;
故选:C.
【点睛】本题考查了相似图形面积比,解题关键是熟记相似图形面积比等于相似比的平方.
5.B
【分析】直接利用位似图形的性质得出线段比进而得出答案.
【详解】解:∵图形甲与图形乙是位似图形,是位似中心,位似比为,
∴,
∵,
∴,
∴
故答案为:B.
【点睛】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
6.A
【分析】是的中点可求得,根据三角形相似的性质可得,可得的长即可求解.
【详解】解:∵是的中点,,
∴,
又∵∽,
,即,
解得,
,
故选:A.
【点睛】本题考查了三角形相似的性质,掌握三角形相似的性质对应边的比相等是解题的关键.
7.见解析
【分析】根据位似图形的定义解答即可.
【详解】(1)、(2)和(4)中的两个图形都是位似图形,(1)中的位似中心是点A,(2)中的位似中心是点P,(4)中的位似中心是点O.
【点睛】本题考查了位似图形的的定义,对应边互相平行(或共线)且每对对应顶点所在的直线都经过同一点的两个相似多边形叫做位似图形.
8.(1)作图见解析
(2)作图见解析
【解析】(1)
解:如图所示,点O即为所求作;
(2)
解:分别连接OA、OB、OC,分别延长2倍,找到对应点、、,将对应点连接起来,即可作出,如图所示:
【点睛】本题考查了网格中作图,熟练掌握网格特征以及位似变换的性质是解题的关键.
9.(1)作图见解析,10;(2)见解析;(3)见解析
【分析】(1)作出且的线段即可;
(2)找出中点,连接即可;
(3)作相似三角形且相似比为1:3,找出边的三等分点F,连接,即可得△ABF的面积是△CBF的面积.
【详解】(1)
因为平行四边形对边平行且相等,故可如图1所示图像,即为平行四边形ABCD,
,,,
,
是直角三角形,
;
(2)
由网格可作矩形BMCN,根据矩形的对角线互相平分,如图2所示E为BC中点,连接AE,则AE为的中线;
(3)
如图3所示,作,使,取的3等分点H,作交于点F,则,且相似比1:3,
,
,
与同高,
△ABF的面积是△CBF的面积.
【点睛】本题考查作图-应用与设计作图,平行线分线段成比例,解题关键是理解题意,运用所学知识解题.
10.(1),;(2),;(3)260
【分析】(1)延长DG交BE于M,交AB于N,证明△DAG≌△BAE,根据全等三角形的性质得到BE=DG,∠ADG=∠ABE,根据三角形内角和定理得到BE⊥DG;
(2)设与交于,与交于点,由比的性质求出、的值,由相似三角形的判定证得,由相似三角形的性质得出,,根据三角形和内角和定理得出,即;
(3)连接EG、BD,由(2)得出,,且,由勾股定理求得、的值,由即可得出结论.
【详解】(1)延长DG交BE于M,交AB于 N,如图2,
∵四边形ABCD、四边形EFGA为正方形,
∴AB=AD,AE=AG,∠DAB=∠GAE=90°,
∴∠DAB-∠BAG=∠GAE-∠BAG,
即 ∠DAG=∠BAE,
在△DAG和△BAE中,
∴△DAG≌△BAE(SAS),
∴BE=DG,∠ADG=∠ABE,
∵∠AND=∠BNM,
∴∠BMN=∠NAD=90°,即BE⊥DG,
故答案为:;;
(2),,理由如下:
设与交于,与交于点,如图3,
∵,,,
∴,.
∵四边形和四边形为矩形,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴.
(3)连接EG、BD,如图3
∵,,,
∴,.
∵四边形和四边形为矩形,
∴
∴,,
由(2)证得
,
∴.
【点睛】本题是相似形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,熟练掌握特殊平行四边形的性质是解题的关键.
11.是位似图形,位似比为.
【分析】四边形和四边形ABCD位似,所以四边形∽四边形ABCD;相似具有传递性,可得四边形∽四边形ABCD;因为位似比等于相似比,据此即可求得四边形和四边形ABCD的位似比.
【详解】∵四边形ABCD和四边形位似,
∴四边形ABCD∽四边形.
∵四边形和四边形位似,
∴四边形∽四边形.
∴四边形∽四边形ABCD.
∵对应顶点的连线过同一点,
∴四边形和四边形ABCD是位似图形.
∵四边形ABCD和四边形位似,位似比=2,
四边形和四边形位似,位似比=1,
∴四边形和四边形ABCD的位似比为.
【点睛】本题考查位似图形的判定方法与性质,解题的关键是要明确位似图形是特殊的相似图形,相似具有传递性.
12.1:2
【分析】由△OAB与△OCD是以点O为位似中心的位似图形,得出相似比解答即可.
【详解】∵△OAB与△OCD是以点O为位似中心的位似图形.
又∵AE、CB分别是△OAB、△OCD的中线,∴相似比是,∴AE:CB=1:2.
故答案为1:2.
【点睛】本题考查了位似变换的性质,正确理解位似与相似的关系进行解答.
13.
【分析】利用位似图形及相似三角形的性质即可解题.
【详解】,
.
∵四边形与四边形位似,
,
,
,
∴四边形与四边形的面积比为,
故答案为:1:9.
【点睛】本题主要考查相似三角形及位似图形的性质,掌握相似三角形和位似图形的性质是关键.
答案第11页,共22页
答案第11页,共22页
课时1位似图形练习题
学校:___________姓名:___________班级:___________
一、单选题
1.下列运动形式中:(1)传动带上的电视机;(2)电梯上的人的升降;(3)照相时底片上的投影与站在照相机前的人;(4)国旗上的红五角星.上述运动形式中不是位似变换的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,在平面直角坐标系中,与是位似图形,则位似中心是( ).
A. B. C. D.
3.如图,与位似,点O是它们的位似中心,其中,若,则DE的长为( )
A.1 B.2 C.4 D.16
4.如图,四边形和四边形是以点O为位似中心的位似图形,若,则四边形与四边形的面积比为( )
A. B. C. D.
5.如图,图形甲与图形乙是位似图形,是位似中心,位似比为,点,的对应点分别为点,.若,则的长为( )
A.8 B.9 C.10 D.15
6.如图,在中,,,是的中点,在上取一点,使∽,则的长是( )
A. B. C. D.
二、解答题
7.指出下列各图中的两个图形是否是位似图形,如果是位似图形,请指出其位似中心.
(1) (2) (3) (4)
8.如图11×7的网格中,每个小正方形的边长均为1个单位长度,点A、B、C都在格点上(两条网格线的交点叫格点)
(1)在线段BC下方用无刻度直尺作出一点O,使得
(2)以O为位似中心,将放大为原来的2倍,得对应,请在网格中作出.
9.如图,是由5×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
(1)在图1中,画出平行四边形ABCD,并直接写出它的面积;
(2)在图2中,画出△ABC的中线AE;
(3)在图3中,在AC上找点F,连结BF,使△ABF的面积是△CBF的面积.
10.背景:一次小组合作探究课上,小明将两个正方形按如图1所示的位置摆放(点、、在同一条直线上),小组讨论后,提出了下列三个问题,请你帮助解答:
(1)如图2,将正方形绕点按逆时针方向旋转,则与的数量关系为___________,位置关系为___________.(直接写出答案)
(2)如图3,把背景中的正方形分别改写成矩形和矩形,且,,,将矩形绕点按顺时针方向旋转,求与的数量关系和位置关系;
(3)在(2)的条件下,小组发现:在旋转过程中,的值是定值,请求出这个定值.(直接写出答案)
11.如图,四边形ABCD和四边形位似,位似比=2,四边形A′B′C′D′和四边形位似,位似比=1.四边形和四边形ABCD是位似图形吗?位似比是多少?
三、填空题
12.如图,△OAB与△OCD是以点O为位似中心的位似图形,点B在OD上,AE、CB分别是△OAB、△OCD的中线,则AE:CB的值为______
13.如图,四边形与四边形位似,点为位似中心.已知,则四边形与四边形的面积比为________.
试卷第11页,共33页
试卷第11页,共33页
参考答案
1.B
【分析】位似变换必须满足对应点的连线相交于一点,由此分析即可.
【详解】解:(1)传动带上的电视机,和(2)电梯上的人的升降;是平移变换;(4)国旗上的红五角星;它们都不满足对应点的连线相交于一点,则不是位似变换;
(3)照相时底片上的投影与站在照相机前的人;满足对应点的连线相交于一点,则它属于位似变换;
故选:B.
【点睛】本题考查位似变换的定义,掌握位似变换的要点是对应点的连线相交于一点是解题关键.
2.B
【分析】找位似图形的位似中心直接连接位似图形的对应点并延长,延长线的交点即所找位似中心,写出坐标即可.
【详解】作图如下:
延长线的交点为(7,0),位似中心即为(7,0).
故选:B.
【点睛】本题考查了找位似图形的位似中心,理解位似中心的定义做出图像是做出本题的关键.
3.B
【分析】根据位似图形的性质得出位似比,进而得出DE的长.
【详解】解:∵△ABC与△DEF位似,点O是它们的位似中心,其中OA:OD=2:1,
∴AB:DE=2:1,
∵AB=4,
∴DE的长为:2.
故选:B.
【点睛】本题考查的是位似变换,正确掌握位似图形的性质是解题关键.
4.C
【分析】根据面积比是相似比的平方直接求解即可.
【详解】解:四边形和四边形是以点为位似中心的位似图形, ,
则四边形与四边形的相似比为:,
∴四边形与四边形的面积比为;
故选:C.
【点睛】本题考查了相似图形面积比,解题关键是熟记相似图形面积比等于相似比的平方.
5.B
【分析】直接利用位似图形的性质得出线段比进而得出答案.
【详解】解:∵图形甲与图形乙是位似图形,是位似中心,位似比为,
∴,
∵,
∴,
∴
故答案为:B.
【点睛】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
6.A
【分析】是的中点可求得,根据三角形相似的性质可得,可得的长即可求解.
【详解】解:∵是的中点,,
∴,
又∵∽,
,即,
解得,
,
故选:A.
【点睛】本题考查了三角形相似的性质,掌握三角形相似的性质对应边的比相等是解题的关键.
7.见解析
【分析】根据位似图形的定义解答即可.
【详解】(1)、(2)和(4)中的两个图形都是位似图形,(1)中的位似中心是点A,(2)中的位似中心是点P,(4)中的位似中心是点O.
【点睛】本题考查了位似图形的的定义,对应边互相平行(或共线)且每对对应顶点所在的直线都经过同一点的两个相似多边形叫做位似图形.
8.(1)作图见解析
(2)作图见解析
【解析】(1)
解:如图所示,点O即为所求作;
(2)
解:分别连接OA、OB、OC,分别延长2倍,找到对应点、、,将对应点连接起来,即可作出,如图所示:
【点睛】本题考查了网格中作图,熟练掌握网格特征以及位似变换的性质是解题的关键.
9.(1)作图见解析,10;(2)见解析;(3)见解析
【分析】(1)作出且的线段即可;
(2)找出中点,连接即可;
(3)作相似三角形且相似比为1:3,找出边的三等分点F,连接,即可得△ABF的面积是△CBF的面积.
【详解】(1)
因为平行四边形对边平行且相等,故可如图1所示图像,即为平行四边形ABCD,
,,,
,
是直角三角形,
;
(2)
由网格可作矩形BMCN,根据矩形的对角线互相平分,如图2所示E为BC中点,连接AE,则AE为的中线;
(3)
如图3所示,作,使,取的3等分点H,作交于点F,则,且相似比1:3,
,
,
与同高,
△ABF的面积是△CBF的面积.
【点睛】本题考查作图-应用与设计作图,平行线分线段成比例,解题关键是理解题意,运用所学知识解题.
10.(1),;(2),;(3)260
【分析】(1)延长DG交BE于M,交AB于N,证明△DAG≌△BAE,根据全等三角形的性质得到BE=DG,∠ADG=∠ABE,根据三角形内角和定理得到BE⊥DG;
(2)设与交于,与交于点,由比的性质求出、的值,由相似三角形的判定证得,由相似三角形的性质得出,,根据三角形和内角和定理得出,即;
(3)连接EG、BD,由(2)得出,,且,由勾股定理求得、的值,由即可得出结论.
【详解】(1)延长DG交BE于M,交AB于 N,如图2,
∵四边形ABCD、四边形EFGA为正方形,
∴AB=AD,AE=AG,∠DAB=∠GAE=90°,
∴∠DAB-∠BAG=∠GAE-∠BAG,
即 ∠DAG=∠BAE,
在△DAG和△BAE中,
∴△DAG≌△BAE(SAS),
∴BE=DG,∠ADG=∠ABE,
∵∠AND=∠BNM,
∴∠BMN=∠NAD=90°,即BE⊥DG,
故答案为:;;
(2),,理由如下:
设与交于,与交于点,如图3,
∵,,,
∴,.
∵四边形和四边形为矩形,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴.
(3)连接EG、BD,如图3
∵,,,
∴,.
∵四边形和四边形为矩形,
∴
∴,,
由(2)证得
,
∴.
【点睛】本题是相似形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,熟练掌握特殊平行四边形的性质是解题的关键.
11.是位似图形,位似比为.
【分析】四边形和四边形ABCD位似,所以四边形∽四边形ABCD;相似具有传递性,可得四边形∽四边形ABCD;因为位似比等于相似比,据此即可求得四边形和四边形ABCD的位似比.
【详解】∵四边形ABCD和四边形位似,
∴四边形ABCD∽四边形.
∵四边形和四边形位似,
∴四边形∽四边形.
∴四边形∽四边形ABCD.
∵对应顶点的连线过同一点,
∴四边形和四边形ABCD是位似图形.
∵四边形ABCD和四边形位似,位似比=2,
四边形和四边形位似,位似比=1,
∴四边形和四边形ABCD的位似比为.
【点睛】本题考查位似图形的判定方法与性质,解题的关键是要明确位似图形是特殊的相似图形,相似具有传递性.
12.1:2
【分析】由△OAB与△OCD是以点O为位似中心的位似图形,得出相似比解答即可.
【详解】∵△OAB与△OCD是以点O为位似中心的位似图形.
又∵AE、CB分别是△OAB、△OCD的中线,∴相似比是,∴AE:CB=1:2.
故答案为1:2.
【点睛】本题考查了位似变换的性质,正确理解位似与相似的关系进行解答.
13.
【分析】利用位似图形及相似三角形的性质即可解题.
【详解】,
.
∵四边形与四边形位似,
,
,
,
∴四边形与四边形的面积比为,
故答案为:1:9.
【点睛】本题主要考查相似三角形及位似图形的性质,掌握相似三角形和位似图形的性质是关键.
答案第11页,共22页
答案第11页,共22页
