2022-2023学年人教版九年级下27.3 课时2 平面直角坐标系中的位似 练习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级下27.3 课时2 平面直角坐标系中的位似 练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 428.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版九年级下第二十七章位似
课时2平面直角坐标系中的位似练习题
学校:___________姓名:___________班级:___________
一、单选题
1.如图,在ABC中,D、E分别为线段BC、BA的中点,设ABC的面积为S,EBD的面积为S.则=( )
A. B. C. D.
2.已知△ABC与是以原点为中心的位似图形,且A(3,1),△ABC与的相似比为,则A的对应点的坐标是( )
A.(6,2) B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2) D.(2,6)
3.如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是( )
A.(﹣1,2) B.(﹣3,1)
C.(﹣3,﹣1)或(3,1) D.(﹣1,2)或(1,﹣2)
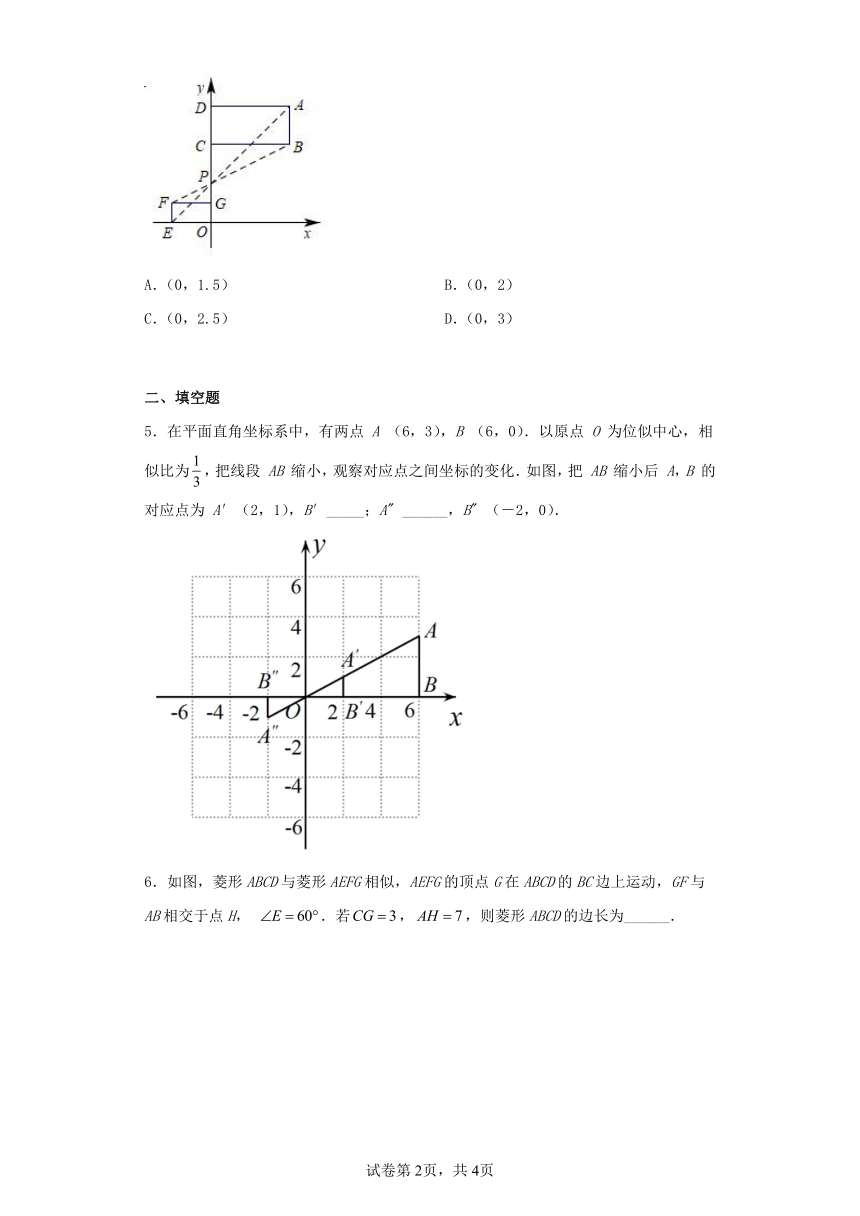
4.如图,在直角坐标系xOy中,矩形EFGO的两边OE,OG在坐标轴上,以y轴上的某一点P为位似中心,作矩形ABCD,使其与矩形EFGO位似,若点B,F的坐标分别为(4,4),(-2,1),则位似中心P的坐标为( )
A.(0,1.5) B.(0,2)
C.(0,2.5) D.(0,3)
二、填空题
5.在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为,把线段 AB 缩小,观察对应点之间坐标的变化.如图,把 AB 缩小后 A,B 的对应点为 A′(2,1),B′_____;A" ______,B" (-2,0).
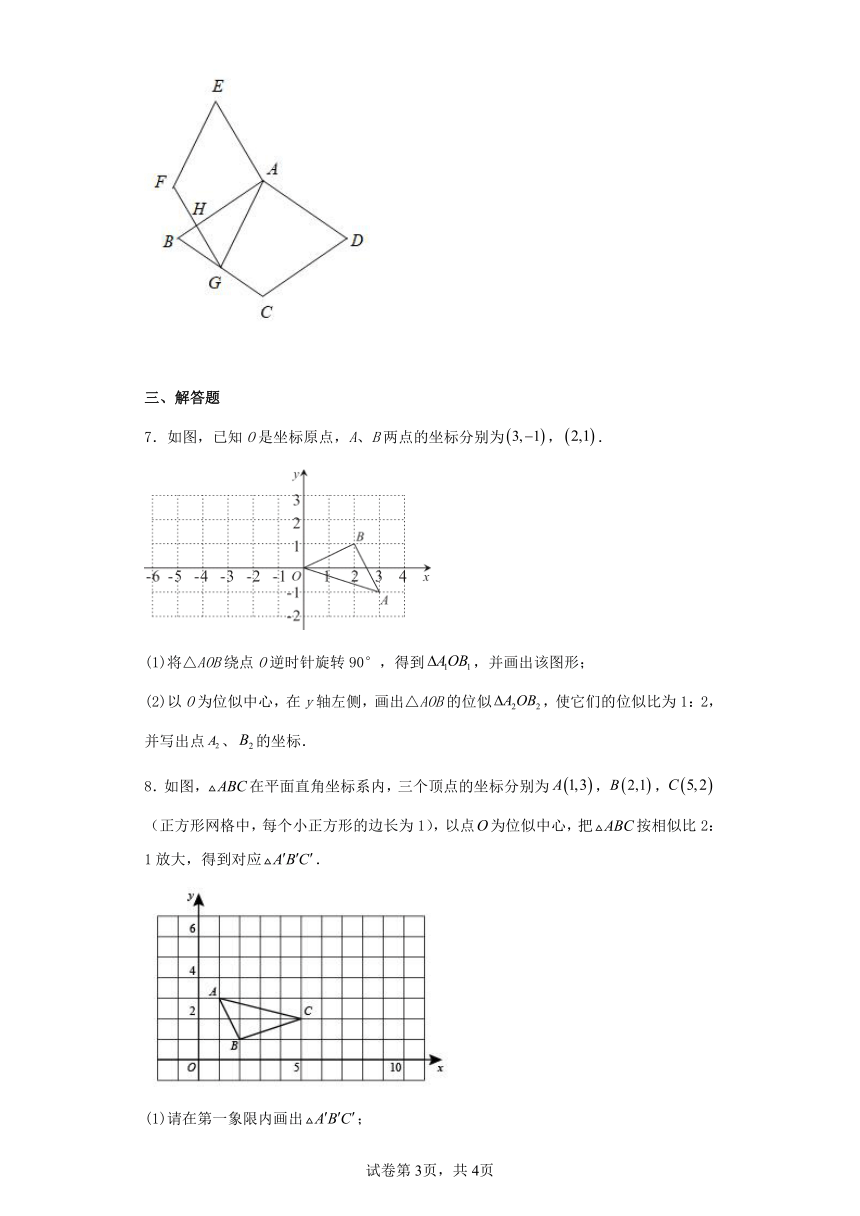
6.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H, .若,,则菱形ABCD的边长为______.
三、解答题
7.如图,已知O是坐标原点,A、B两点的坐标分别为,.
(1)将△AOB绕点O逆时针旋转90°,得到,并画出该图形;
(2)以O为位似中心,在y轴左侧,画出△AOB的位似,使它们的位似比为1:2,并写出点、的坐标.
8.如图,在平面直角坐标系内,三个顶点的坐标分别为,,(正方形网格中,每个小正方形的边长为1),以点为位似中心,把按相似比2:1放大,得到对应.
(1)请在第一象限内画出;
(2)若以点、、、为顶点的四边形是平行四边形,请直接写出满足条件的点的坐标.
试卷第11页,共33页
试卷第11页,共33页
参考答案:
1.B
【分析】先判定,得到相似比为,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.
【详解】解:∵D、E分别为线段BC、BA的中点,
∴,
又∵,
∴,相似比为,
∴,
故选:B.
【点睛】此题考查相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
2.C
【分析】根据位似图形对应点坐标与位似比之间的关系进行求解即可.
【详解】解:∵△ABC与是以原点为中心的位似图形,A(3,1),△ABC与的相似比为,
∴点A的对应点的坐标为(3×2,1×2)或(-2×3,-2×1),即(6,2)或(﹣6,﹣2),
故选:C.
【点睛】本题主要考查了位似图形对应点坐标,熟知两个以原点为位似中心的位似图形位似比为k,则点A(x,y)的对应点坐标为(,)或(,)是解题的关键.
3.C
【分析】在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,据此求解即可得.
【详解】解:以原点O为位似中心,相似比为,把△AOB缩小,点B的坐标为则点B的对应点B'的坐标为或,即或
故选:C.
【点睛】题目主要考查位似变换的性质,理解运用其性质是解题关键.
4.B
【分析】根据题意求出CG的长,利用相似三角形的性质求出PG的值,从而求出点P的坐标即可.
【详解】解:∵四边形ABCD和四边形EFGO均为矩形,点B,F的坐标分别为(4,4)、(-2,1),
∴,,点C(0,4),点G(0,1),
∴,,
∵,
∴△FGP∽△BCP
∴,即,
解得,
∴点P坐标为(0,2),
故选:B.
【点睛】此题主要考查了位似中心的概念和位似图形的性质等知识,熟练掌握位似中心的概念和位似图形的性质是解题的关键.
5. (2 ,0 ) (-2,-1)
【解析】略
6.9
【分析】连接AC,首先证明△ABC是等边三角形,再证明△BGH∽△CAG,推出,由此构建方程即可解决问题.
【详解】解:连接AC.
∵菱形ABCD∽菱形AEFG,
∴∠B=∠E=∠AGF=60°,AB=BC,
∴△ABC是等边三角形,设AB=BC=AC=a,则BH=a-7,BG=a-3,
∴∠ACB=60°,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,
∵∠AGH=∠ACG=60°,
∴∠BGH=∠CAG,
∵∠B=∠ACG,
∴△BGH∽△CAG,
∴,
∴,
∴a2-10a+9=0,
∴a=9或1(舍弃),
∴AB=9,
故答案为:9.
【点睛】本题考查相似多边形的性质,等边三角形的性质,菱形的性质等知识,解题的关键是正确寻找相似三角形解决问题.
7.(1)见解析
(2)画图见解析,,
【分析】(1)根据题意作图即可;
(2)先根据题意作图,然后写出相应点的坐标即可.
(1)
解:如图所示,即为所求;
(2)
解:如图所示,即为所求,,
【点睛】本题主要考查了画旋转图形,画位似图形,坐标与图形,熟知相关知识是解题的关键.
8.(1)见解析
(2);;
【分析】(1)根据点为位似中心,,,,把按相似比2:1放大,得到对应,求出点,,的坐标,在网格中描点顺次连线即得;
(2)设D(x,y),根据平行四边形的对角线互相平分与,,,得到当AC为对角线时, x+2=1+5,y+1=2+3,推出x=4,y=4,得到;当BC是对角线时,推出x+1=2+5,x=6,y+3=1+2,y=0,得到,当AB为对角线时,推出x+5=1+2,x=-2,y+2=3+1,y=2,得到.
(1)
∵点为位似中心,按相似比2:1放大,得到对应,
∴,
∵,,,
∴(2,6),(4,2),(10,4),
在网格图中顺次连接各点得到,如图;
(2)
设D(x,y),
∵平行四边形的对角线互相平分,且,,,
∴当AC为对角线时,AC中点的横坐标为,纵坐标为,BD中点的横坐标为,纵坐标为,
∴x+2=1+5,y+1=2+3,
∴x=4,y=4,
∴,
同理,
当BC是对角线时,x+1=2+5,x=6,y+3=1+2,y=0,
∴,
当AB为对角线时,x+5=1+2,x=-2,y+2=3+1,y=2,
∴,
综上,;;.
【点睛】本题主要考查了位似三角形,平行四边形,解决问题的关键是熟练掌握位似三角形的定义及画法,平行四边形对角线的性质和线段中点坐标公式.
答案第11页,共22页
答案第11页,共22页
课时2平面直角坐标系中的位似练习题
学校:___________姓名:___________班级:___________
一、单选题
1.如图,在ABC中,D、E分别为线段BC、BA的中点,设ABC的面积为S,EBD的面积为S.则=( )
A. B. C. D.
2.已知△ABC与是以原点为中心的位似图形,且A(3,1),△ABC与的相似比为,则A的对应点的坐标是( )
A.(6,2) B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2) D.(2,6)
3.如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是( )
A.(﹣1,2) B.(﹣3,1)
C.(﹣3,﹣1)或(3,1) D.(﹣1,2)或(1,﹣2)
4.如图,在直角坐标系xOy中,矩形EFGO的两边OE,OG在坐标轴上,以y轴上的某一点P为位似中心,作矩形ABCD,使其与矩形EFGO位似,若点B,F的坐标分别为(4,4),(-2,1),则位似中心P的坐标为( )
A.(0,1.5) B.(0,2)
C.(0,2.5) D.(0,3)
二、填空题
5.在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为,把线段 AB 缩小,观察对应点之间坐标的变化.如图,把 AB 缩小后 A,B 的对应点为 A′(2,1),B′_____;A" ______,B" (-2,0).
6.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H, .若,,则菱形ABCD的边长为______.
三、解答题
7.如图,已知O是坐标原点,A、B两点的坐标分别为,.
(1)将△AOB绕点O逆时针旋转90°,得到,并画出该图形;
(2)以O为位似中心,在y轴左侧,画出△AOB的位似,使它们的位似比为1:2,并写出点、的坐标.
8.如图,在平面直角坐标系内,三个顶点的坐标分别为,,(正方形网格中,每个小正方形的边长为1),以点为位似中心,把按相似比2:1放大,得到对应.
(1)请在第一象限内画出;
(2)若以点、、、为顶点的四边形是平行四边形,请直接写出满足条件的点的坐标.
试卷第11页,共33页
试卷第11页,共33页
参考答案:
1.B
【分析】先判定,得到相似比为,再根据两个相似三角形的面积比等于相似比的平方,据此解题即可.
【详解】解:∵D、E分别为线段BC、BA的中点,
∴,
又∵,
∴,相似比为,
∴,
故选:B.
【点睛】此题考查相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
2.C
【分析】根据位似图形对应点坐标与位似比之间的关系进行求解即可.
【详解】解:∵△ABC与是以原点为中心的位似图形,A(3,1),△ABC与的相似比为,
∴点A的对应点的坐标为(3×2,1×2)或(-2×3,-2×1),即(6,2)或(﹣6,﹣2),
故选:C.
【点睛】本题主要考查了位似图形对应点坐标,熟知两个以原点为位似中心的位似图形位似比为k,则点A(x,y)的对应点坐标为(,)或(,)是解题的关键.
3.C
【分析】在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,据此求解即可得.
【详解】解:以原点O为位似中心,相似比为,把△AOB缩小,点B的坐标为则点B的对应点B'的坐标为或,即或
故选:C.
【点睛】题目主要考查位似变换的性质,理解运用其性质是解题关键.
4.B
【分析】根据题意求出CG的长,利用相似三角形的性质求出PG的值,从而求出点P的坐标即可.
【详解】解:∵四边形ABCD和四边形EFGO均为矩形,点B,F的坐标分别为(4,4)、(-2,1),
∴,,点C(0,4),点G(0,1),
∴,,
∵,
∴△FGP∽△BCP
∴,即,
解得,
∴点P坐标为(0,2),
故选:B.
【点睛】此题主要考查了位似中心的概念和位似图形的性质等知识,熟练掌握位似中心的概念和位似图形的性质是解题的关键.
5. (2 ,0 ) (-2,-1)
【解析】略
6.9
【分析】连接AC,首先证明△ABC是等边三角形,再证明△BGH∽△CAG,推出,由此构建方程即可解决问题.
【详解】解:连接AC.
∵菱形ABCD∽菱形AEFG,
∴∠B=∠E=∠AGF=60°,AB=BC,
∴△ABC是等边三角形,设AB=BC=AC=a,则BH=a-7,BG=a-3,
∴∠ACB=60°,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,
∵∠AGH=∠ACG=60°,
∴∠BGH=∠CAG,
∵∠B=∠ACG,
∴△BGH∽△CAG,
∴,
∴,
∴a2-10a+9=0,
∴a=9或1(舍弃),
∴AB=9,
故答案为:9.
【点睛】本题考查相似多边形的性质,等边三角形的性质,菱形的性质等知识,解题的关键是正确寻找相似三角形解决问题.
7.(1)见解析
(2)画图见解析,,
【分析】(1)根据题意作图即可;
(2)先根据题意作图,然后写出相应点的坐标即可.
(1)
解:如图所示,即为所求;
(2)
解:如图所示,即为所求,,
【点睛】本题主要考查了画旋转图形,画位似图形,坐标与图形,熟知相关知识是解题的关键.
8.(1)见解析
(2);;
【分析】(1)根据点为位似中心,,,,把按相似比2:1放大,得到对应,求出点,,的坐标,在网格中描点顺次连线即得;
(2)设D(x,y),根据平行四边形的对角线互相平分与,,,得到当AC为对角线时, x+2=1+5,y+1=2+3,推出x=4,y=4,得到;当BC是对角线时,推出x+1=2+5,x=6,y+3=1+2,y=0,得到,当AB为对角线时,推出x+5=1+2,x=-2,y+2=3+1,y=2,得到.
(1)
∵点为位似中心,按相似比2:1放大,得到对应,
∴,
∵,,,
∴(2,6),(4,2),(10,4),
在网格图中顺次连接各点得到,如图;
(2)
设D(x,y),
∵平行四边形的对角线互相平分,且,,,
∴当AC为对角线时,AC中点的横坐标为,纵坐标为,BD中点的横坐标为,纵坐标为,
∴x+2=1+5,y+1=2+3,
∴x=4,y=4,
∴,
同理,
当BC是对角线时,x+1=2+5,x=6,y+3=1+2,y=0,
∴,
当AB为对角线时,x+5=1+2,x=-2,y+2=3+1,y=2,
∴,
综上,;;.
【点睛】本题主要考查了位似三角形,平行四边形,解决问题的关键是熟练掌握位似三角形的定义及画法,平行四边形对角线的性质和线段中点坐标公式.
答案第11页,共22页
答案第11页,共22页
