2023年广东省中考数学考前热身训练(五)(含解析)
文档属性
| 名称 | 2023年广东省中考数学考前热身训练(五)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 419.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 18:53:48 | ||
图片预览



文档简介
2023年广东省中考数学考前热身训练(五)
一.选择题(共10小题,每小题3分,共30分)
1.下列四个数中,的倒数是( )
A.3 B. C. D.﹣3
2.长江是我国第一大河,它的全长约为6300千米,6300这个数用科学记数法表示为( )
A.63×102 B.6.3×102 C.6.3×103 D.6.3×104
3.下列四个几何体中,从正面看是三角形的是( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C.(a+b)2=a2+b2 D.(﹣4a3b)2=16a6b
5.如图,在△ABC中,D,E分别是边AB,AC上的点,且AD=2,BD=1,DE∥BC,则下列说法不正确的是( )
A.AE:EC=2:1 B.△ADE∽△ABC
C.DEBC D.S△ADE:S△ABC=2:3
6.为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.平均数是3.8 B.样本为20名学生
C.中位数是3 D.众数是6
7.若关于x的一元二次方程x2+x﹣k=0有两个实数根,则k的取值范围是( )
A.k B.k C.k D.k
8.实数a在数轴上的对应点的位置如图所示,那么下列结论正确的是( )
A.|a|>1 B.﹣a<1
C.a+1>0 D.1
9.如图,在直角坐标系中,菱形ABCD顶点A,B,C在坐标轴上,若点B的坐标为
(﹣1,0),∠ABC=60°,将△AOB绕点O顺时针旋转得到△A'OB',当A'恰好第一次落在线段OD上时,B′的坐标为( )
A.() B.()
C.() D.()
10.如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B'OC',点C'在OA上,则边BC扫过区域(图中阴影部分)的面积为( )
A. B.
C. D.
二.填空题(共5小题,每小题3分,共15分)
11.甲、乙、丙3名学生随机排成一排拍照,其中甲排在中间的概率是 .
12.多项式x2﹣6x分解因式的结果是 .
13.已知一个正多边形的一个外角为36°,则这个正多边形的边数是 .
14.学校科技兴趣小组为探索如图所示的电路中电压U(V)、电流I(A)、电阻R(Ω)三者之间的关系,测得数据如下,根据数据猜想得到三者之间为:I.由此可得,当电阻R=110Ω甲选时,
电流I= A.
15.如图,在平面直角坐标系中,已知点A(8,0),点B为y轴正半轴上一动点,连接AB,以AB为边在AB下方作等边三角形ABC,连接OC,则OC的最小值为 .
三.解答题(一)(共3小题,每小题8分,共24分)
16.解不等式组:.
17.(1)计算:(﹣2023)0+2sin60°+|2|;
(2)先化简,再求值:,a.
18.端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:
(1)该商场节后每千克A粽子的进价是多少元?
(2)如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?
四.解答题(二)(共3小题,每小题9分,共27分)
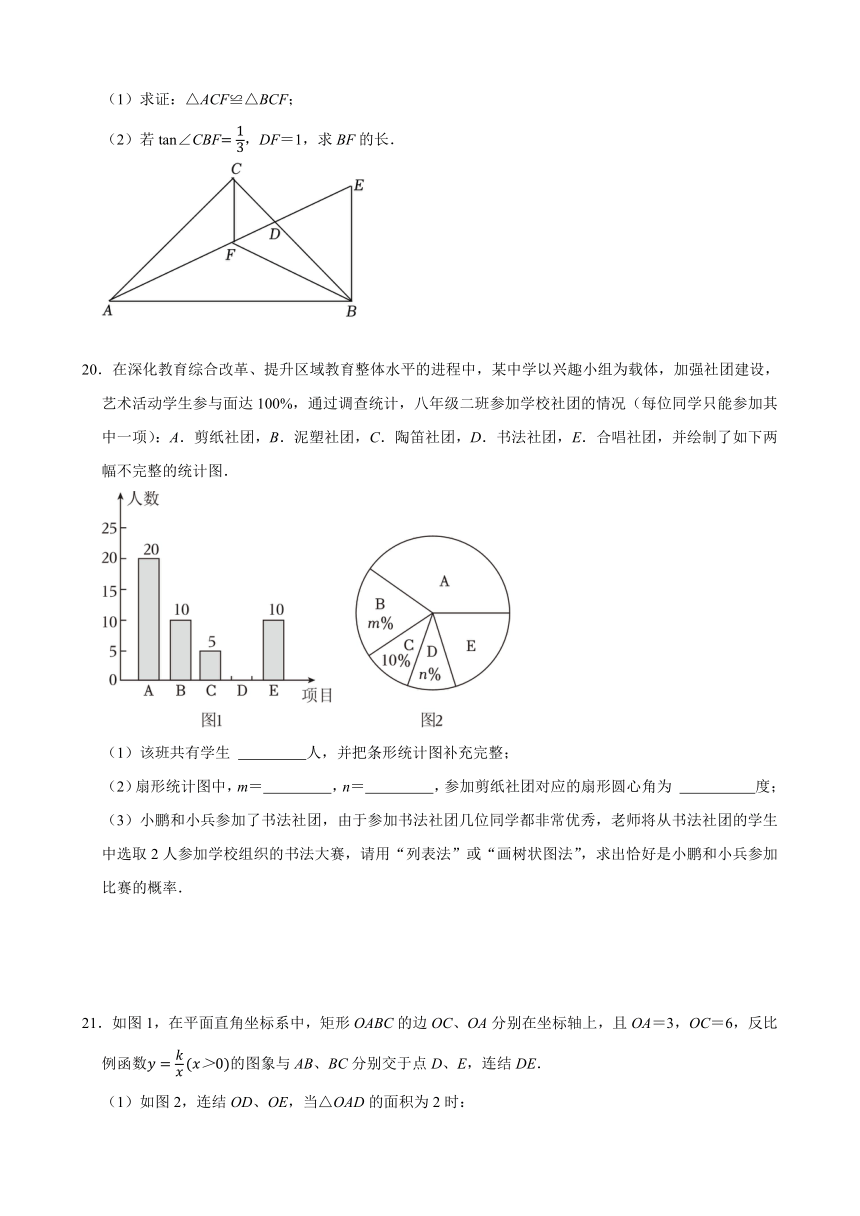
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上一点,BE⊥AB交AD的延长线于点E,点F是AE的中点,连接CF,BF.
(1)求证:△ACF≌△BCF;
(2)若tan∠CBF,DF=1,求BF的长.
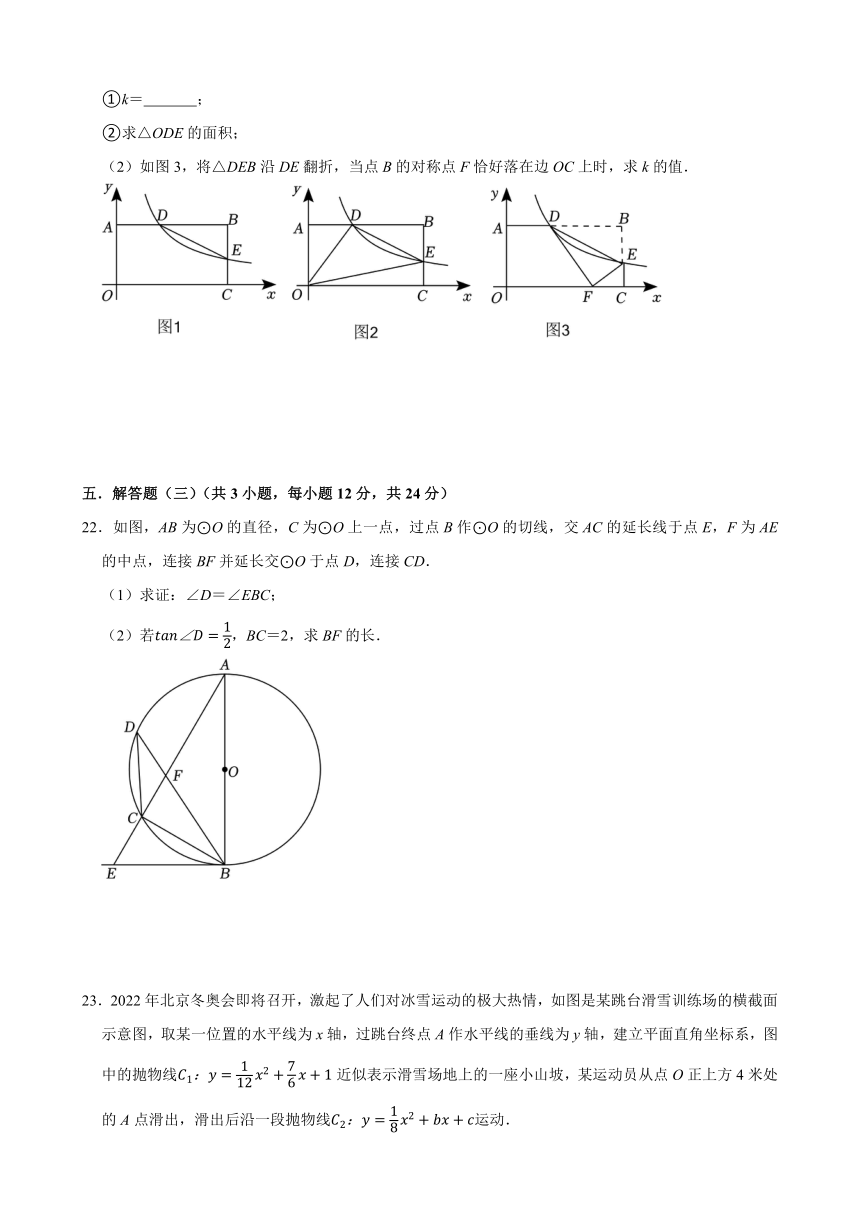
20.在深化教育综合改革、提升区域教育整体水平的进程中,某中学以兴趣小组为载体,加强社团建设,艺术活动学生参与面达100%,通过调查统计,八年级二班参加学校社团的情况(每位同学只能参加其中一项):A.剪纸社团,B.泥塑社团,C.陶笛社团,D.书法社团,E.合唱社团,并绘制了如下两幅不完整的统计图.
(1)该班共有学生 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ,参加剪纸社团对应的扇形圆心角为 度;
(3)小鹏和小兵参加了书法社团,由于参加书法社团几位同学都非常优秀,老师将从书法社团的学生中选取2人参加学校组织的书法大赛,请用“列表法”或“画树状图法”,求出恰好是小鹏和小兵参加比赛的概率.
21.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
五.解答题(三)(共3小题,每小题12分,共24分)
22.如图,AB为⊙O的直径,C为⊙O上一点,过点B作⊙O的切线,交AC的延长线于点E,F为AE的中点,连接BF并延长交⊙O于点D,连接CD.
(1)求证:∠D=∠EBC;
(2)若,BC=2,求BF的长.
23.2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.
2023年广东省中考数学考前热身训练(五)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:的倒数是﹣3,
故选:D.
2.【解答】解:6300=6.3×103,
故选:C.
3.【解答】解:A.主视图为长方形,不符合题意;
B.主视图为三角形,符合题意;
C.主视图为长方形,不符合题意;
D.主视图为长方形,不符合题意.
故选:B.
4.【解答】解:A、3,不合题意;
B、20220﹣()﹣2=1﹣4=﹣3,符合题意;
C、(a+b)2=a2+2ab+b2,不合题意;
D、(﹣4a3b)2=16a6b2,不合题意;
故选:B.
5.【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∴2,DEBC,
∴S△ADE:S△ABC=4:9.
故选项A,B,C正确,
故选:D.
6.【解答】解:A.平均数为(2×3+3×6+4×5+5×4+6×2)=3.8(个),此选项说法正确,符合题意;
B.样本为20名学生的编织数量,此选项说法错误,不符合题意;
C.共20个数据,从小到大排列后位于第10个和第11个的数据分别是4和4,
∴中位数为4,此选项说法错误,不符合题意;
D.众数是3,此选项说法错误,不符合题意;
故选:A.
7.【解答】解:∵关于x的一元二次方程x2+x﹣k=0有两个实数根,
∴Δ=12﹣4×1×(﹣k)≥0,
解得k,
故选:B.
8.【解答】解:A、a<﹣1,所以|a|>1,故此选项正确;
B、﹣a=|a|,|a|>1,所以﹣a>1,故此选项不正确;
C、a+1取绝对值较大数的符号,由A知,取a的符号,是负数,故此选项不正确;
D、a<﹣1,所以﹣10,故此选项不正确.
故选:A.
9.【解答】解:将△AOB绕点O顺时针旋转得到△A'OB',A'恰好第一次落在线段OD上,如图所示:
过点B′作B′E⊥OB于点E,
则∠OEB′=90°,∠AOD+∠AOB′=∠AOB,OB′=OB,
∵∠AOB′+∠EOB′=∠AOB,
∴∠AOD=∠EOB′,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵A、B、C在坐标轴上,
∴AO⊥BC,
∴OA⊥AD,
∴∠AOB=∠OAD=90°,
∴∠OAD=∠EOB′,
又∵∠AOD=∠EOB′,
∴△AOD∽△EOB′,
∴,
∵点B的坐标为(﹣1,0),∠ABC=60°,
∴OB=OB′=1,∠BAO=90°﹣60°=30°,
∴AD=AB=2OB=2,
在Rt△AOB中,由勾股定理得:OA,
在Rt△OAD中,由勾股定理得:OD,
∴B′E,OE,
∴B′(,),
故选:D.
10.【解答】解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO=△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′cm,
∴B′C′(cm),
∴S扇形B′OB(cm2),
S扇形C′OC(cm2),
∴阴影部分面积=S扇形B′OB+S△B′C′O﹣S△BCO﹣S扇形C′OC=S扇形B′OB﹣S扇形C′OC(cm2);
故选:B.
二.填空题(共5小题)
11.【解答】解:∵甲、乙、丙3名学生随机排成一排拍照,共有甲乙丙、甲丙乙、乙甲丙、乙丙甲、丙甲乙、丙乙甲这6种等可能结果,
而甲排在中间的只有2种结果,
∴甲排在中间的概率为,
故答案为:
12.【解答】解:x2﹣6x=x(x﹣6).
故答案为:x(x﹣6).
13.【解答】解:正多边形的边数是:360°÷36°=10.
故答案为:10.
14.【解答】解:由题意可得,
I,
由表格可知:当R=220时,I=1,
∴1,
解得U=220,
∴I,
当R=110时,I2,
故答案为:2.
15.【解答】解:如图,以OA为对称轴作等边△AMN,延长CN交x轴于E,
∵△ABC是等边三角形,△AMN是等边三角形,
∴AM=AN,AB=AC,∠MAN=∠BAC,∠AMN=60°=∠ANM,
∴∠BAM=∠CAN,
∴△ANC≌△AMB(SAS),
∴∠AMB=∠ANC=60°,
∴∠ENO=60°,
∵AO=6,∠AMB=60°,AO⊥BO,
∴MO=NO,
∵∠ENO=60°,∠EON=90°,
∴∠AEN=30°,EOON=8,
∴点C在EN上移动,
∴当OC'⊥EN时,OC'有最小值,
此时,O'CEO=4,
故答案为:4.
三.解答题(共8小题)
16.【解答】解:,
解不等式①得:x<1,
解不等式②得:x>﹣2,
∴原不等式组的解集为:﹣2<x<1.
17.【解答】解:(1)原式=4﹣1+22
=4﹣12
=5;
(2)原式
,
当a时,
原式.
18.【解答】解:(1)设该商场节后每千克A粽子的进价为x元,
根据题意,得,
解得x=10或x=﹣12(舍去),
经检验,x=10是原分式方程的根,且符合题意,
答:该商场节后每千克A粽子的进价是10元;
(2)设该商场节前购进m千克A粽子,总利润为w元,
根据题意,得12m+10(400﹣m)≤4600,
解得m≤300,
w=(20﹣12)m+(16﹣10)(400﹣m)=2m+2400,
∵2>0,
∴w随着m增大而增大,
当m=300时,w取得最大值,最大利润为2×300+2400=3000(元),
答:该商场节前购进300千克A粽子获得利润最大,最大利润是3000元.
19.【解答】(1)证明:∵BE⊥AB,
∴∠ABE=90°,
∵点F是AE的中点,
∴BF=AF=EF,
在△ACF和△BCF中,
,
∴△ACF≌△BCF(SSS);
(2)解:∵△ACF≌△BCF,
∴∠CBF=∠CAF,
∴tan∠CAF=tan∠CBF,
Rt△ACD中,,即,
∴,
由(1)可知∠ACF=∠BCF=45°,
又∠CBA=∠CBE=45°,
∴∠BCF=∠CBE,
∴CF∥BE,
∴△CFD∽△BED,
∴,
∵DF=1
∴DE=2,
∴EF=3,
∴BF=3.
20.【解答】解:(1)该班共有学生人数为:5÷10%=50(人),
则D的人数为:50﹣20﹣10﹣5﹣10=5(人),
故答案为:50,
把条形统计图补充完整如下:
(2)∵m%=10÷50×100%=20%,n%=5÷50×100%=10%,
∴m=20,n=10,
参加剪纸社团对应的扇形圆心角为:360°144°,
故答案为:20,10,144;
(3)把小鹏和小兵分别记为a、b,其他3位同学分别记为c、d、e,
画树状图如下:
共有20种等可能的结果,其中恰好是小鹏和小兵参加比赛的结果有2种,
∴恰好是小鹏和小兵参加比赛的概率为.
21.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
22.【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵BE是⊙O的切线,
∴∠ABE=90°,
∴∠ABC+∠CBE=90°,
∴∠A=∠CBE,
∵∠A=∠D,
∴∠D=∠EBC;
(2)解:∵∠,
∴tanA=tan∠CBE,
∴,
∴AC=4,CE=1,
∴AE=AC+CE=5,
∵F为AE的中点,
∴BFAE.
23.【解答】解:(1)由题意可知抛物线C2:yx2+bx+c过点(0,4)和(4,8),将其代入得:
,解得:,
∴抛物线C2的函数解析式为:yx2x+4;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
m2m+4﹣(m2m+1)=1,
整理得:(m﹣12)(m+4)=0,
解得:m1=12,m2=﹣4(舍去),
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3)C1:yx2x+1(x﹣7)2,
当x=7时,运动员到达坡顶,
即72+7b+4>3,
解得:b.
一.选择题(共10小题,每小题3分,共30分)
1.下列四个数中,的倒数是( )
A.3 B. C. D.﹣3
2.长江是我国第一大河,它的全长约为6300千米,6300这个数用科学记数法表示为( )
A.63×102 B.6.3×102 C.6.3×103 D.6.3×104
3.下列四个几何体中,从正面看是三角形的是( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C.(a+b)2=a2+b2 D.(﹣4a3b)2=16a6b
5.如图,在△ABC中,D,E分别是边AB,AC上的点,且AD=2,BD=1,DE∥BC,则下列说法不正确的是( )
A.AE:EC=2:1 B.△ADE∽△ABC
C.DEBC D.S△ADE:S△ABC=2:3
6.为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.平均数是3.8 B.样本为20名学生
C.中位数是3 D.众数是6
7.若关于x的一元二次方程x2+x﹣k=0有两个实数根,则k的取值范围是( )
A.k B.k C.k D.k
8.实数a在数轴上的对应点的位置如图所示,那么下列结论正确的是( )
A.|a|>1 B.﹣a<1
C.a+1>0 D.1
9.如图,在直角坐标系中,菱形ABCD顶点A,B,C在坐标轴上,若点B的坐标为
(﹣1,0),∠ABC=60°,将△AOB绕点O顺时针旋转得到△A'OB',当A'恰好第一次落在线段OD上时,B′的坐标为( )
A.() B.()
C.() D.()
10.如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B'OC',点C'在OA上,则边BC扫过区域(图中阴影部分)的面积为( )
A. B.
C. D.
二.填空题(共5小题,每小题3分,共15分)
11.甲、乙、丙3名学生随机排成一排拍照,其中甲排在中间的概率是 .
12.多项式x2﹣6x分解因式的结果是 .
13.已知一个正多边形的一个外角为36°,则这个正多边形的边数是 .
14.学校科技兴趣小组为探索如图所示的电路中电压U(V)、电流I(A)、电阻R(Ω)三者之间的关系,测得数据如下,根据数据猜想得到三者之间为:I.由此可得,当电阻R=110Ω甲选时,
电流I= A.
15.如图,在平面直角坐标系中,已知点A(8,0),点B为y轴正半轴上一动点,连接AB,以AB为边在AB下方作等边三角形ABC,连接OC,则OC的最小值为 .
三.解答题(一)(共3小题,每小题8分,共24分)
16.解不等式组:.
17.(1)计算:(﹣2023)0+2sin60°+|2|;
(2)先化简,再求值:,a.
18.端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:
(1)该商场节后每千克A粽子的进价是多少元?
(2)如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?
四.解答题(二)(共3小题,每小题9分,共27分)
19.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上一点,BE⊥AB交AD的延长线于点E,点F是AE的中点,连接CF,BF.
(1)求证:△ACF≌△BCF;
(2)若tan∠CBF,DF=1,求BF的长.
20.在深化教育综合改革、提升区域教育整体水平的进程中,某中学以兴趣小组为载体,加强社团建设,艺术活动学生参与面达100%,通过调查统计,八年级二班参加学校社团的情况(每位同学只能参加其中一项):A.剪纸社团,B.泥塑社团,C.陶笛社团,D.书法社团,E.合唱社团,并绘制了如下两幅不完整的统计图.
(1)该班共有学生 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ,参加剪纸社团对应的扇形圆心角为 度;
(3)小鹏和小兵参加了书法社团,由于参加书法社团几位同学都非常优秀,老师将从书法社团的学生中选取2人参加学校组织的书法大赛,请用“列表法”或“画树状图法”,求出恰好是小鹏和小兵参加比赛的概率.
21.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
五.解答题(三)(共3小题,每小题12分,共24分)
22.如图,AB为⊙O的直径,C为⊙O上一点,过点B作⊙O的切线,交AC的延长线于点E,F为AE的中点,连接BF并延长交⊙O于点D,连接CD.
(1)求证:∠D=∠EBC;
(2)若,BC=2,求BF的长.
23.2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情,如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.
2023年广东省中考数学考前热身训练(五)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:的倒数是﹣3,
故选:D.
2.【解答】解:6300=6.3×103,
故选:C.
3.【解答】解:A.主视图为长方形,不符合题意;
B.主视图为三角形,符合题意;
C.主视图为长方形,不符合题意;
D.主视图为长方形,不符合题意.
故选:B.
4.【解答】解:A、3,不合题意;
B、20220﹣()﹣2=1﹣4=﹣3,符合题意;
C、(a+b)2=a2+2ab+b2,不合题意;
D、(﹣4a3b)2=16a6b2,不合题意;
故选:B.
5.【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∴2,DEBC,
∴S△ADE:S△ABC=4:9.
故选项A,B,C正确,
故选:D.
6.【解答】解:A.平均数为(2×3+3×6+4×5+5×4+6×2)=3.8(个),此选项说法正确,符合题意;
B.样本为20名学生的编织数量,此选项说法错误,不符合题意;
C.共20个数据,从小到大排列后位于第10个和第11个的数据分别是4和4,
∴中位数为4,此选项说法错误,不符合题意;
D.众数是3,此选项说法错误,不符合题意;
故选:A.
7.【解答】解:∵关于x的一元二次方程x2+x﹣k=0有两个实数根,
∴Δ=12﹣4×1×(﹣k)≥0,
解得k,
故选:B.
8.【解答】解:A、a<﹣1,所以|a|>1,故此选项正确;
B、﹣a=|a|,|a|>1,所以﹣a>1,故此选项不正确;
C、a+1取绝对值较大数的符号,由A知,取a的符号,是负数,故此选项不正确;
D、a<﹣1,所以﹣10,故此选项不正确.
故选:A.
9.【解答】解:将△AOB绕点O顺时针旋转得到△A'OB',A'恰好第一次落在线段OD上,如图所示:
过点B′作B′E⊥OB于点E,
则∠OEB′=90°,∠AOD+∠AOB′=∠AOB,OB′=OB,
∵∠AOB′+∠EOB′=∠AOB,
∴∠AOD=∠EOB′,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵A、B、C在坐标轴上,
∴AO⊥BC,
∴OA⊥AD,
∴∠AOB=∠OAD=90°,
∴∠OAD=∠EOB′,
又∵∠AOD=∠EOB′,
∴△AOD∽△EOB′,
∴,
∵点B的坐标为(﹣1,0),∠ABC=60°,
∴OB=OB′=1,∠BAO=90°﹣60°=30°,
∴AD=AB=2OB=2,
在Rt△AOB中,由勾股定理得:OA,
在Rt△OAD中,由勾股定理得:OD,
∴B′E,OE,
∴B′(,),
故选:D.
10.【解答】解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO=△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′cm,
∴B′C′(cm),
∴S扇形B′OB(cm2),
S扇形C′OC(cm2),
∴阴影部分面积=S扇形B′OB+S△B′C′O﹣S△BCO﹣S扇形C′OC=S扇形B′OB﹣S扇形C′OC(cm2);
故选:B.
二.填空题(共5小题)
11.【解答】解:∵甲、乙、丙3名学生随机排成一排拍照,共有甲乙丙、甲丙乙、乙甲丙、乙丙甲、丙甲乙、丙乙甲这6种等可能结果,
而甲排在中间的只有2种结果,
∴甲排在中间的概率为,
故答案为:
12.【解答】解:x2﹣6x=x(x﹣6).
故答案为:x(x﹣6).
13.【解答】解:正多边形的边数是:360°÷36°=10.
故答案为:10.
14.【解答】解:由题意可得,
I,
由表格可知:当R=220时,I=1,
∴1,
解得U=220,
∴I,
当R=110时,I2,
故答案为:2.
15.【解答】解:如图,以OA为对称轴作等边△AMN,延长CN交x轴于E,
∵△ABC是等边三角形,△AMN是等边三角形,
∴AM=AN,AB=AC,∠MAN=∠BAC,∠AMN=60°=∠ANM,
∴∠BAM=∠CAN,
∴△ANC≌△AMB(SAS),
∴∠AMB=∠ANC=60°,
∴∠ENO=60°,
∵AO=6,∠AMB=60°,AO⊥BO,
∴MO=NO,
∵∠ENO=60°,∠EON=90°,
∴∠AEN=30°,EOON=8,
∴点C在EN上移动,
∴当OC'⊥EN时,OC'有最小值,
此时,O'CEO=4,
故答案为:4.
三.解答题(共8小题)
16.【解答】解:,
解不等式①得:x<1,
解不等式②得:x>﹣2,
∴原不等式组的解集为:﹣2<x<1.
17.【解答】解:(1)原式=4﹣1+22
=4﹣12
=5;
(2)原式
,
当a时,
原式.
18.【解答】解:(1)设该商场节后每千克A粽子的进价为x元,
根据题意,得,
解得x=10或x=﹣12(舍去),
经检验,x=10是原分式方程的根,且符合题意,
答:该商场节后每千克A粽子的进价是10元;
(2)设该商场节前购进m千克A粽子,总利润为w元,
根据题意,得12m+10(400﹣m)≤4600,
解得m≤300,
w=(20﹣12)m+(16﹣10)(400﹣m)=2m+2400,
∵2>0,
∴w随着m增大而增大,
当m=300时,w取得最大值,最大利润为2×300+2400=3000(元),
答:该商场节前购进300千克A粽子获得利润最大,最大利润是3000元.
19.【解答】(1)证明:∵BE⊥AB,
∴∠ABE=90°,
∵点F是AE的中点,
∴BF=AF=EF,
在△ACF和△BCF中,
,
∴△ACF≌△BCF(SSS);
(2)解:∵△ACF≌△BCF,
∴∠CBF=∠CAF,
∴tan∠CAF=tan∠CBF,
Rt△ACD中,,即,
∴,
由(1)可知∠ACF=∠BCF=45°,
又∠CBA=∠CBE=45°,
∴∠BCF=∠CBE,
∴CF∥BE,
∴△CFD∽△BED,
∴,
∵DF=1
∴DE=2,
∴EF=3,
∴BF=3.
20.【解答】解:(1)该班共有学生人数为:5÷10%=50(人),
则D的人数为:50﹣20﹣10﹣5﹣10=5(人),
故答案为:50,
把条形统计图补充完整如下:
(2)∵m%=10÷50×100%=20%,n%=5÷50×100%=10%,
∴m=20,n=10,
参加剪纸社团对应的扇形圆心角为:360°144°,
故答案为:20,10,144;
(3)把小鹏和小兵分别记为a、b,其他3位同学分别记为c、d、e,
画树状图如下:
共有20种等可能的结果,其中恰好是小鹏和小兵参加比赛的结果有2种,
∴恰好是小鹏和小兵参加比赛的概率为.
21.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
22.【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵BE是⊙O的切线,
∴∠ABE=90°,
∴∠ABC+∠CBE=90°,
∴∠A=∠CBE,
∵∠A=∠D,
∴∠D=∠EBC;
(2)解:∵∠,
∴tanA=tan∠CBE,
∴,
∴AC=4,CE=1,
∴AE=AC+CE=5,
∵F为AE的中点,
∴BFAE.
23.【解答】解:(1)由题意可知抛物线C2:yx2+bx+c过点(0,4)和(4,8),将其代入得:
,解得:,
∴抛物线C2的函数解析式为:yx2x+4;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
m2m+4﹣(m2m+1)=1,
整理得:(m﹣12)(m+4)=0,
解得:m1=12,m2=﹣4(舍去),
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3)C1:yx2x+1(x﹣7)2,
当x=7时,运动员到达坡顶,
即72+7b+4>3,
解得:b.
同课章节目录
