2022—2023学年北师大版数学八年级下册 第6章平行四边形期末复习试卷(含答案)
文档属性
| 名称 | 2022—2023学年北师大版数学八年级下册 第6章平行四边形期末复习试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 20:06:14 | ||
图片预览




文档简介
2023年北师大版数学八年级下册
《平行四边形》期末复习试卷
一、选择题
1.□ABCD中,∠A:∠B=1:2,则∠C的度数为( ).
A.30° B.45° C.60° D.120°
2.如图,平行四边形ABCD中,∠ABC平分线交AD于E,∠BED=155°,则∠A度数为( )
A.155° B.130° C.125° D.110°
3.如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,
则△DEF周长为( )
A.9 B.10 C.11 D.12
4.一个正多边形的每个外角都是36°,这个正多边形是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
5.若一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.7 B.8 C.9 D.10
6.一个多边形内角和是1080 ,则这个多边形的对角线条数为 ( )
A.26 B. 24 C.22 D.20
7.下列条件不能判断四边形是平行四边形的是( )
A.两组对边分别相等
B.一组对边平行且相等
C.一组对边平行,另一组对边相等
D.对角线互相平分
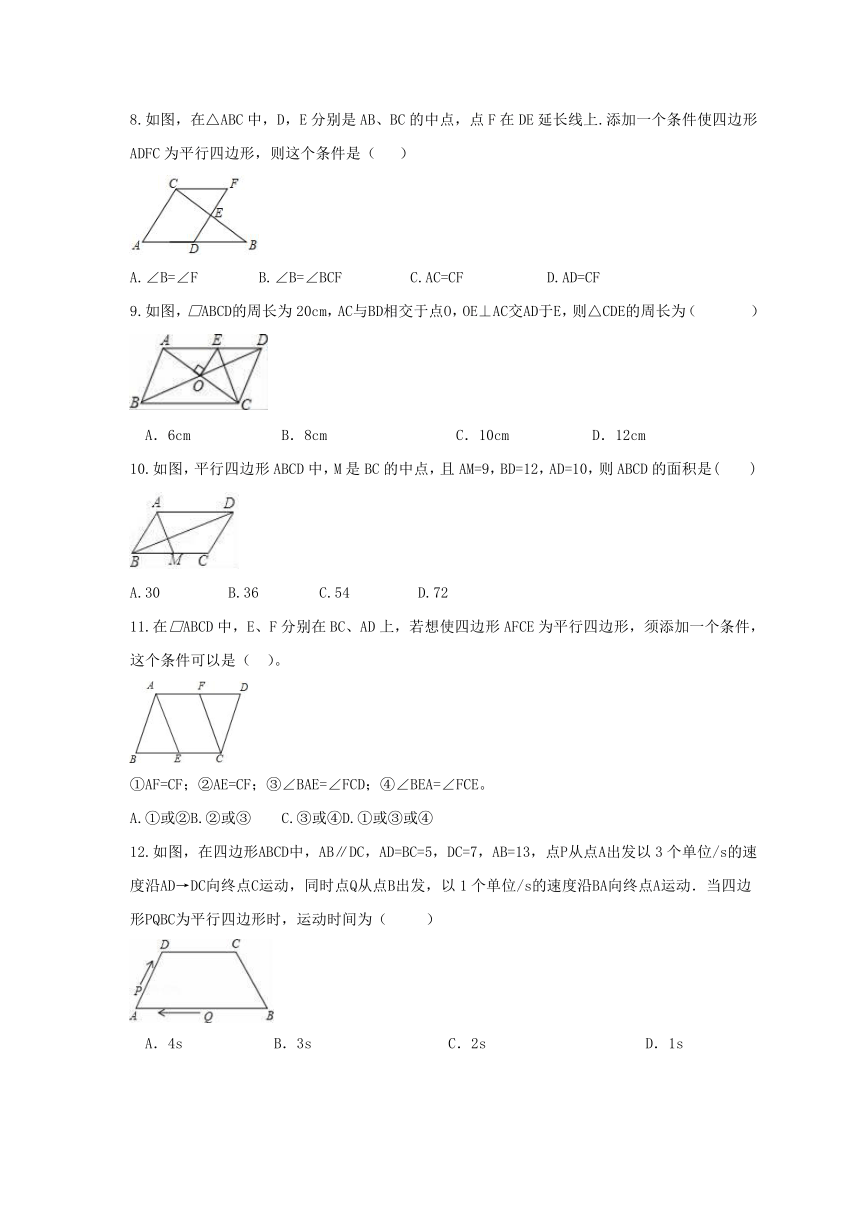
8.如图,在△ABC中,D,E分别是AB、BC的中点,点F在DE延长线上.添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
9.如图,□ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
A.6cm B.8cm C.10cm D.12cm
10.如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )
A.30 B.36 C.54 D.72
11.在□ABCD中,E、F分别在BC、AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )。
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A.①或② B.②或③ C.③或④ D.①或③或④
12.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
二、填空题
13.如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD= .
14.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,DE为△ABC的中位线,延长BC至F,使CF=BC,连接FE并延长交AB于点M.若BC=a,则△FMB的周长为 .
15.如图,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
16.在四边形ABCD中,已知∠A=∠C=60°,则当∠B的度数为__________时,四边形ABCD是平行四边形.
17.如图,□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
18.如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,
则当△PBC为直角三角形时,BP的长为 .
三、解答题
19.一个多边形的内角和比四边形的内角和多540°并且这个多边形的各个内角都相等,这个多边形的每个内角等于几度?
20.如图,在 ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
21.如图,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
22.如图,□ABCD的周长为16cm,它的对角线AC和BD相交于点O,OE⊥AC交AD于E,求△DCE的周长.
23.如图,在□ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
24.如图,在△ABC中,AB=AC,延长BC至点D,使CD=BC,点E在边AC上,以CE,CD为邻边作 CDFE,过点C作CG∥AB交EF于点G.连结BG,DE.
(1)∠ACB与∠GCD有怎样的数量关系?请说明理由;
(2)求证:△BCG≌△DCE.
25.如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB于点E、F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其它条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB和直线BC于E、F和G.试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).
参考答案
1.C.
2.B.
3.A
4.C
5.B
6.D
7.C.
8.B;
9.C
10.D.
11.C;
12.B
13.答案为:2.
14.答案为:4.5a.
15.答案为:BE=DF或BF=DE或∠BAE=∠DCF
16.答案为:20°
17.答案为:118.解:分两种情况:
(1)①当∠BPC=90°时,作AM⊥BC于M,如图1所示,
∵∠B=60°,∴∠BAM=30°,∴BM=AB=1,
∴AM=BM=,CM=BC﹣BM=4﹣1=3,
∴AC==2,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,
∴当点P与A重合时,∠BPC=∠BAC=90°,∴BP=BA=2;
②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,BP==2;
(2)当∠BCP=90°时,如图3所示:则CP=AM=,∴BP=;
综上所述:当△PBC为直角三角形时,BP的长为 2或2或.
19.略
20.(1)解:∵在 ABCD中,DE平分∠ADC交AB于点G,BF平分∠ABC交AD的延长线于F,
∴∠1=∠2,∠3=∠4,AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5.
∵AB=8,∴BG=8﹣5=3;
(2)证明:∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵DE平分∠ADC,∴∠2=∠ADC.
∵BF平分∠ABC,∴∠4=∠ABC,∴∠2=∠4.
∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.
∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.
21.证明:∵四边形ABCD是平行四边形ABCD,
∴OA=OC,DF∥EB∴∠E=∠F
又∵∠EOA=∠FOC
∴△OAE≌△OCF,∴OE=OF
22.解:∵平行四边形的对角线互相平分,∴OA=OC,
又∵OE⊥AC于O,∴AE=CE,
∵平行四边形ABCD的周长为16cm,∴AD+DC=8cm,
∴△DCE的周长=DE+CE+DC=AD+DC=8cm.
23.证明:∵四边形ABCD是平行四边形,
∴点O是BD的中点.
又∵点E是边CD的中点,
∴OE是△BCD的中位线.
∴OE∥BC,且OE=BC.
又∵CF=BC,
∴OE=CF.
又∵点F在BC的延长线上,
∴OE∥CF.
∴四边形OCFE是平行四边形.
24.解:(1)∠ACB=∠GCD.理由如下:
∵AB=AC,
∴∠ABC=∠ACB.
∵CG∥AB,
∴∠ABC=∠GCD,
∴∠ACB=∠GCD.
(2)证明:∵四边形CDFE是平行四边形,
∴EF∥CD,
∴∠ACB=∠GEC,∠EGC=∠GCD.
∵∠ACB=∠GCD,
∴∠GEC=∠EGC,
∴EC=GC.
∵∠GCD=∠ACB,
∴∠GCB=∠ECD.
∵BC=DC,
∴△BCG≌△DCE.
25.解:(1)DE+DF=AB.理由如下:
如图1.∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵DF∥AC,
∴∠FDB=∠C,
∵AB=AC,
∴∠C=∠B,
∴∠FDB=∠B,
∴DF=FB,
∴DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在CB延长线上时,如图2①,AB=DE﹣DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图2②,AB=DF﹣DE;
(3)如图3,AB=DE+DG+DF.
《平行四边形》期末复习试卷
一、选择题
1.□ABCD中,∠A:∠B=1:2,则∠C的度数为( ).
A.30° B.45° C.60° D.120°
2.如图,平行四边形ABCD中,∠ABC平分线交AD于E,∠BED=155°,则∠A度数为( )
A.155° B.130° C.125° D.110°
3.如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,
则△DEF周长为( )
A.9 B.10 C.11 D.12
4.一个正多边形的每个外角都是36°,这个正多边形是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
5.若一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.7 B.8 C.9 D.10
6.一个多边形内角和是1080 ,则这个多边形的对角线条数为 ( )
A.26 B. 24 C.22 D.20
7.下列条件不能判断四边形是平行四边形的是( )
A.两组对边分别相等
B.一组对边平行且相等
C.一组对边平行,另一组对边相等
D.对角线互相平分
8.如图,在△ABC中,D,E分别是AB、BC的中点,点F在DE延长线上.添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
9.如图,□ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
A.6cm B.8cm C.10cm D.12cm
10.如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )
A.30 B.36 C.54 D.72
11.在□ABCD中,E、F分别在BC、AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )。
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A.①或② B.②或③ C.③或④ D.①或③或④
12.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
二、填空题
13.如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD= .
14.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,DE为△ABC的中位线,延长BC至F,使CF=BC,连接FE并延长交AB于点M.若BC=a,则△FMB的周长为 .
15.如图,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
16.在四边形ABCD中,已知∠A=∠C=60°,则当∠B的度数为__________时,四边形ABCD是平行四边形.
17.如图,□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
18.如图, ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,
则当△PBC为直角三角形时,BP的长为 .
三、解答题
19.一个多边形的内角和比四边形的内角和多540°并且这个多边形的各个内角都相等,这个多边形的每个内角等于几度?
20.如图,在 ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
21.如图,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
22.如图,□ABCD的周长为16cm,它的对角线AC和BD相交于点O,OE⊥AC交AD于E,求△DCE的周长.
23.如图,在□ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
24.如图,在△ABC中,AB=AC,延长BC至点D,使CD=BC,点E在边AC上,以CE,CD为邻边作 CDFE,过点C作CG∥AB交EF于点G.连结BG,DE.
(1)∠ACB与∠GCD有怎样的数量关系?请说明理由;
(2)求证:△BCG≌△DCE.
25.如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB于点E、F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其它条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB和直线BC于E、F和G.试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).
参考答案
1.C.
2.B.
3.A
4.C
5.B
6.D
7.C.
8.B;
9.C
10.D.
11.C;
12.B
13.答案为:2.
14.答案为:4.5a.
15.答案为:BE=DF或BF=DE或∠BAE=∠DCF
16.答案为:20°
17.答案为:1
(1)①当∠BPC=90°时,作AM⊥BC于M,如图1所示,
∵∠B=60°,∴∠BAM=30°,∴BM=AB=1,
∴AM=BM=,CM=BC﹣BM=4﹣1=3,
∴AC==2,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,
∴当点P与A重合时,∠BPC=∠BAC=90°,∴BP=BA=2;
②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,BP==2;
(2)当∠BCP=90°时,如图3所示:则CP=AM=,∴BP=;
综上所述:当△PBC为直角三角形时,BP的长为 2或2或.
19.略
20.(1)解:∵在 ABCD中,DE平分∠ADC交AB于点G,BF平分∠ABC交AD的延长线于F,
∴∠1=∠2,∠3=∠4,AB∥DC,
∴∠2=∠AGD,
∴∠1=∠AGD,
∴AD=AG=5.
∵AB=8,∴BG=8﹣5=3;
(2)证明:∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,DC∥AB,AD∥BC.
∵DE平分∠ADC,∴∠2=∠ADC.
∵BF平分∠ABC,∴∠4=∠ABC,∴∠2=∠4.
∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.
∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.
21.证明:∵四边形ABCD是平行四边形ABCD,
∴OA=OC,DF∥EB∴∠E=∠F
又∵∠EOA=∠FOC
∴△OAE≌△OCF,∴OE=OF
22.解:∵平行四边形的对角线互相平分,∴OA=OC,
又∵OE⊥AC于O,∴AE=CE,
∵平行四边形ABCD的周长为16cm,∴AD+DC=8cm,
∴△DCE的周长=DE+CE+DC=AD+DC=8cm.
23.证明:∵四边形ABCD是平行四边形,
∴点O是BD的中点.
又∵点E是边CD的中点,
∴OE是△BCD的中位线.
∴OE∥BC,且OE=BC.
又∵CF=BC,
∴OE=CF.
又∵点F在BC的延长线上,
∴OE∥CF.
∴四边形OCFE是平行四边形.
24.解:(1)∠ACB=∠GCD.理由如下:
∵AB=AC,
∴∠ABC=∠ACB.
∵CG∥AB,
∴∠ABC=∠GCD,
∴∠ACB=∠GCD.
(2)证明:∵四边形CDFE是平行四边形,
∴EF∥CD,
∴∠ACB=∠GEC,∠EGC=∠GCD.
∵∠ACB=∠GCD,
∴∠GEC=∠EGC,
∴EC=GC.
∵∠GCD=∠ACB,
∴∠GCB=∠ECD.
∵BC=DC,
∴△BCG≌△DCE.
25.解:(1)DE+DF=AB.理由如下:
如图1.∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∴DE=AF.
∵DF∥AC,
∴∠FDB=∠C,
∵AB=AC,
∴∠C=∠B,
∴∠FDB=∠B,
∴DF=FB,
∴DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在CB延长线上时,如图2①,AB=DE﹣DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图2②,AB=DF﹣DE;
(3)如图3,AB=DE+DG+DF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
