小学数学 人教版 五年级上册5_简易方程本单元综合与测试(共132张PPT)
文档属性
| 名称 | 小学数学 人教版 五年级上册5_简易方程本单元综合与测试(共132张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览










文档简介
(共132张PPT)
5 简易方程
数学配人教版
(五年级/上册)
第1课时 用字母表示数(1)
第2课时 用字母表示数(2)
第3课时 用字母表示数(3)
第4课时 用字母表示数(4)
第5课时 用字母表示数(5)
第6课时 方程的意义
第7课时 等式的性质
第8课时 解方程(1)
第9课时 解方程(2)
第10课时 解方程(3)
第11课时 解方程(4)
第12课时 解方程(5)
第13课时 实际问题与方程(1)
第14课时 实际问题与方程(2)
第15课时 实际问题与方程(3)
第16课时 实际问题与方程(4)
第17课时 实际问题与方程(5)
第18课时 整理和复习
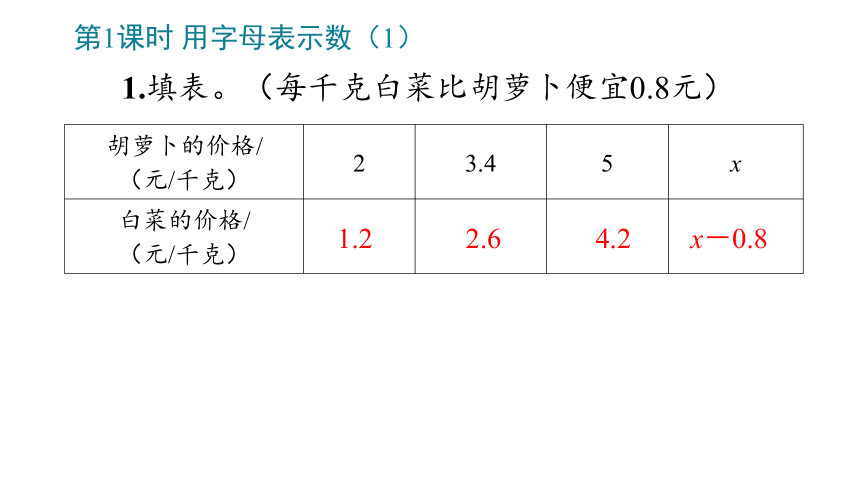
胡萝卜的价格/ (元/千克) 2 3.4 5 x
白菜的价格/ (元/千克)
1.填表。(每千克白菜比胡萝卜便宜0.8元)
第1课时 用字母表示数(1)
1.2
2.6
4.2
x-0.8
0.48÷0.16= 0.4×3.5×2=
0.45×0.6= 15÷1.5=
1.36÷0.4= 0.8+0.8÷4=
2.每课速算。
第1课时 用字母表示数(1)
3
2.8
0.27
10
3.4
1
3.填空题。
(1)某水库的水位高度为h m,水位上升2 m后的高度为( )m。
(2)学校图书馆计划购进图书a本,实际比计划多购进b本,实际购进图书( )本。
第1课时 用字母表示数(1)
h+2
a+b
(3)手套每双16.8元,帽子每顶m元,围巾每条n元。
①买一双手套和一顶帽子花费( )元。
②一双手套比一条围巾便宜( )元。
(4)五(1)班有a人,五(2)班有b人。
①a-b表示( )。
②a÷b表示( )。
五(1)班比五(2)班多多少人
五(1)班的人数是五(2)班的多少倍
第1课时 用字母表示数(1)
n-16.8
16.8+m
4.五(1)班有男生x人,女生比男生少5人。
(1)用含有字母的式子表示五(1)班女生的人数、全班的人数。
女生的人数:x-5
全班的人数:2x-5
第1课时 用字母表示数(1)
(2)当x=23时,五(1)班女生有多少人?全班有多少人?
当x=23时,
x-5
=23-5
=18
2x-5
=23×2-5
=46-5
=41
答:五(1)班女生有18人,全班有41人。
第1课时 用字母表示数(1)
5.一辆公共汽车上原有16个人,到站后下去m人,又上来n人。
(1)用含有字母的式子表示现在车上有多少人。
16-m+n
第1课时 用字母表示数(1)
(2)当m=5,n=7时,现在车上有多少人?
当m=5,n=7时,
16-m+n
=16-5+7
=11+7
=18
答:现在车上有18人。
第1课时 用字母表示数(1)
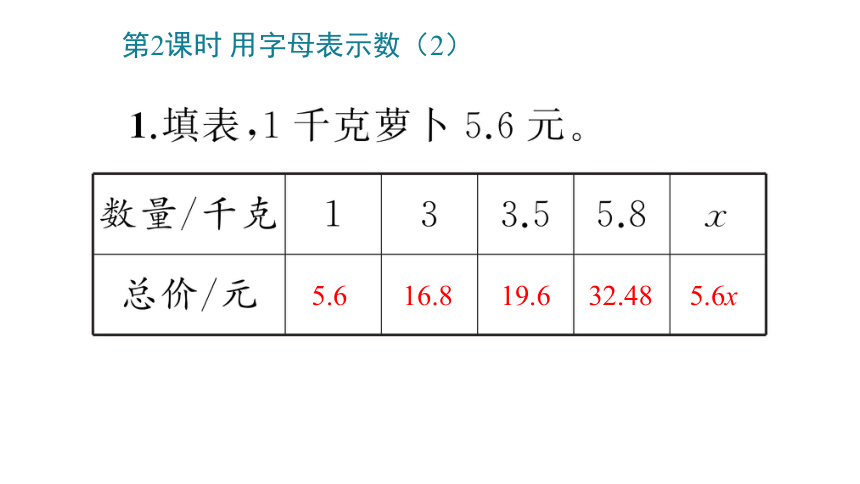
第2课时 用字母表示数(2)
5.6
16.8
19.6
32.48
5.6x
2.省略乘号,写出下列算式。
x×30= a×b=
1×d= x×8.2 × y=
第2课时 用字母表示数(2)
30x
8.2xy
ab
d
3.填空题。
(1)小莉每天练20个大字,m天练( )个大字。
(2)书店卖出30本童话书,一共卖了a元,每本童话书的售价是( )元。
(3)一种花布每米25.6元,买x m这样的花布应付( )元
第2课时 用字母表示数(2)
20m
a÷30
25.6x
(4)有x名同学,平均分成6组,每组有( )名同学。
(5)商店卖出21台手机,每台手机的售价是x元,商店一共卖了( )元。
第2课时 用字母表示数(2)
x÷6
21x
4.判断题。(对的画“√”,错的画“×”)
(1)x+x+x+x+x=5x( )
(2)x×7=7x( )
(3)x÷2=2x( )
第2课时 用字母表示数(2)
√
×
√
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(1)苹果共有多少千克?
用字母写出数量关系式:_______________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
ac
当a = 15,c =5时,
ac = 15×5
= 75
答:苹果共有75kg。
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(2)每箱苹果比桃轻多少千克?
用字母写出数量关系式:_____________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
d-c
当c = 5,d = 6时,
d-c
= 6-5
= 1
答:每箱苹果比桃轻1kg。
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(3)苹果和桃共有多少箱?
用字母写出数量关系式:____________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
a+b
当a = 15,b = 12时,
a+b
= 15+12
= 27
答:苹果和桃共有27箱。
6.不同的汉字代表不同的数字,请你算出下面这些汉字所代表的数字。
1
2
3
第2课时 用字母表示数(2)
1.用字母表示下面图形的周长和面积的计算公式。
第3课时 用字母表示数(3)
C = 2(a+b)
S = ab
C = 4a
S = a2
2.根据运算定律填上适当的数或字母。
(1)a+_____=6+ _____
(2)m+(n+8)=( + )+8
(3)4×x+6×x=( + )×
6
a
m
n
4
6
x
第3课时 用字母表示数(3)
3.把结果相同的算式用线连起来。
第3课时 用字母表示数(3)
4.a表示工作效率,t表示工作时间,c表示工作总量。
(1)用字母表示出它们的数量关系。
c=( )
a=( )
t=( )
at
c÷t
c÷a
第3课时 用字母表示数(3)
(2)张师傅3小时加工240个零件,利用(1)中的公式计算他每小时加工多少个零件。
当t = 3,c = 240时,
a = c÷t
= 240÷3
= 80
答:他每小时加工80个零件。
第3课时 用字母表示数(3)
5.v表示速度,t表示时间,s表示路程。
(1)用字母表示出它们的数量关系。
s=( )
v=( )
t=( )
vt
s÷t
s÷v
第3课时 用字母表示数(3)
(2)一辆汽车每小时行驶56 km,行驶168 km需要多少小时?利用上面的公式计算。
当v = 56,s = 168时,
t = s÷v
= 168÷56
= 3
答:行驶168km需要3小时。
第3课时 用字母表示数(3)
6.a表示单价,x表示数量,c表示总价。
(1)用字母表示出它们的数量关系。
c=( )
a=( )
x=( )
ax
c÷x
c÷a
第3课时 用字母表示数(3)
(2)一盒牛奶5.8元,小明要买6盒,需要花多少钱?利用上面的公式计算。
第3课时 用字母表示数(3)
当a = 5.8,x = 6时,
c = ax
=5.8×6
=34.8
答:需要花34.8元。
7.用含有字母的式子表示下图中阴影部分的面积。
a2+b2
第3课时 用字母表示数(3)
1.用含有字母的式子表示下面的数量关系。
(1)x与8的和。 ( )
(2)比b大8.6的数。 ( )
(3)x 与y的差除以6。 ( )
(4)t的平方加上 12。 ( )
(5)比a 的7倍少3。 ( )
(6)m除以9的商。 ( )
第4课时 用字母表示数(4)
x+8
b+8.6
(x-y)÷ 6
t2+12
7a-3
m ÷ 9
2.每课速算。
0.5
第4课时 用字母表示数(4)
0.2
4
22
3.(1)当x=6.5,y =15.3时,求x +y的值。
(2)当m=45,n=12时,求(m-n)÷3的值
当x= 6.5,y = 15.3时,
x+y
= 6.5+15.3
= 21.8
第4课时 用字母表示数(4)
当m = 45,n = 12时,
(m-n)÷3
= (45-12)÷3
= 33÷3
= 11
4.钢笔每支a元,铅笔每支b元。
(1)买2支钢笔和5支铅笔共需要花 元。
(2)当a=8,b=2时,买2支钢笔和5支铅笔共需要花多少钱?
第4课时 用字母表示数(4)
2a+5b
当a=8,b=2时,
2a+5b
=2×8+5×2
=16+10
=26
答:买2支钢笔和5支铅笔共需要花26元。
5.水果店原来有60 kg苹果,又运来16箱苹果,每箱重x kg。
(1)用式子表示水果店现在有多少千克苹果。
(2)当x=8时,水果店一共有多少千克苹果?
60+16x
当x=8时,
60+16x
=60+16×8
=60+128
=188
答:水果店一共有188 kg苹果。
第4课时 用字母表示数(4)
6.当x=4时,x2和3x各等于多少?当x的值是多少时,x2和3x相等?
第4课时 用字母表示数(4)
第4课时 用字母表示数(4)
当x=4时,
x2 =4×4
= 16
3x =3×4
=12
当x=0或x=3时,x2=3x
答:当x=4时,x2 等于16,3x 等于12。
当x= 0或x=3时,x2 和3x 相等。
1.用小棒摆图形。
(1)摆x个正方形和x个长方形,一共要用多少根小棒?
第5课时 用字母表示数(5)
4x+6x = 10x
答:一共要用10x根小棒。
(2)当x=10时,一共要用多少根小棒?
第5课时 用字母表示数(5)
当x = 10时,
10x = 10×10
= 100
答:一共要用100根小棒。
2.客车的速度是65千米/时,货车的速度是55千米/时。
(1)行驶t小时,两车一共行驶多少千米?当t=5时,两车一共行驶多少千米?
65t+55t = 120t
当t = 5时,
120t =120×5
= 600
答:行驶t小时,两车一共行驶120t km,当t=5时,两车一共行驶600km。
第5课时 用字母表示数(5)
(2)行驶t小时,客车比货车多行驶多少千米?当t=4时,客车比货车多行驶多少千米?
65t-55t = 10t
当t = 4时,
10t = 10×4
= 40
答:行驶t小时,客车比货车多行驶10t km,当t=4 时,客车比货车多行驶 40km。
第5课时 用字母表示数(5)
3.筑路队铺一条长400 km的公路,已经铺了15天,每天铺a km。
(1)用式子表示已经铺了多少千米。当a=2时,已经铺了多少千米?
15a
当a = 2时,
15a
= 15×2
= 30
第5课时 用字母表示数(5)
答:已经铺了15a km,当a=2时,已经铺了30km。
(2)用式子表示还剩多少千米没铺。当a=3时,还剩多少千米没铺?
400-15a
当a = 3时,
400-15a
= 400-15×3
= 400-45
= 355
答:还剩(400-15a)km没铺,当a=3时,还剩355km没铺。
第5课时 用字母表示数(5)
4.
(1)像这样摆下去,摆n个六边形需要( )根小棒。
1+5n
第5课时 用字母表示数(5)
4.
(2)当n=20时,用第(1)题的式子计算摆20个六边形需要的小棒数。
当n = 20时,
1+5n
= 1+5×20
= 1+100
= 101
第5课时 用字母表示数(5)
答:摆20个六边形需要101根小棒。
1.下面哪些式子是方程?在方程后面的括号里画“√”。
2×9=3×6 ( ) 6+9<3×9 ( )
3x>7+5 ( ) 5y=30-x ( )
a ÷ 0.8=32 ( ) 6m+8 ( )
第6课时 方程的意义
√
√
2.每课速算。
第6课时 方程的意义
3a
13
0.4x
25
0.08b
0.185
11x
0.16
3.判断题。(对的画“√”,错的画“×”)
(1)含有未知数的式子叫作方程。 ( )
(2)5x+1是方程。 ( )
(3)a2一定大于2a。( )
(4)4+8=3y是方程。( )
第6课时 方程的意义
×
×
×
√
4.用方程表示下面的数量关系。
第6课时 方程的意义
5.用方程表示下面数量之间的关系。
(1)有x张书签,平均分给6个小朋友,每个人分到3张。
(2)摩托车每分钟行800 m,x分钟行了2800 m。
第6课时 方程的意义
(3)小菲的体重是a kg,妹妹的体重是36 kg,两人的体重一共是80 kg。
(4)父亲今年n岁,比儿子大28岁,儿子今年6岁。
第6课时 方程的意义
(5)公共汽车上原来有9名乘客,到站后有x名乘客下车,有5名乘客上车,现在车上有12名乘客。
第6课时 方程的意义
1.看图填空。
1个西瓜和( )个石榴的质量相等,两边各放上1个石榴,天平保持平衡。天平两边再各去掉1个石榴,天平仍保持( )。
第7课时 等式的性质
2
平衡
平衡的天平两边的物品质量都扩大到原来的( )倍,天平仍然保持( )。平衡的天平两边的物品质量都缩小到原来的( ),天平仍然保持( )。
第7课时 等式的性质
2
平衡
平衡
2.每课速算。
5.6x
第7课时 等式的性质
1.2
1.18y
0.1
0.01
4m
0.018
3.2x
3.在○里填上适当的运算符号,在括号里填上适当的数,使天平平衡。
第7课时 等式的性质
+ 60
- 20
× 9
÷ 3
第7课时 等式的性质
4.根据等式的性质填空。
(1)x+8=36
x+8-( )=36-8
(2)x-9=43
x-9+( )=43+9
(3)3x=1.2
3x÷( )=1.2÷3
(4)x÷1.5=3.7
x÷1.5×( )=3.7×1.5
8
9
3
1.5
第7课时 等式的性质
5.如果x = y,根据等式的性质填空。
x-3= y-( )
x÷( )= y÷10
3
10
第7课时 等式的性质
6.已知 ○+○+○+○=△+○+○,那么△=( )个○。
2
第7课时 等式的性质
1.解方程,填一填。
第8课时 解方程(1)
2.5
11.3
2.5
2.5
第8课时 解方程(1)
3.6
3.6
15.7
3.6
2.后面括号中哪个x的值是方程的解?请在正确的解上画“√”。
第8课时 解方程(1)
√
√
√
√
3.解方程,带※的题要检验。
125+x=164 x+8.05=10.2
第8课时 解方程(1)快乐导航
解:125+x-125=164-125
x=39
解:x+8.05-8.05=10.2-8.05
x=2.15
※x-15=1.5
第8课时 解方程(1)
解:x-1.5+1.5=1.5+1.5
x=3
检验: 方程左边=x-1.5
=3-1.5
=1.5
=方程右边
所 以,x=3是方程的解。
4.根据题中的数量关系列出方程,并求出方程的解。
第8课时 解方程(1)
解:x-5= 26
x-5+5=26+5
x=31
解:x+4.8=8.2
x+4.8-4.8=8.2-4.8
x=3.4
5.方程方程6.3+x=28. 8与y-x =8的x的值相同,求 y 的值。
第8课时 解方程(1)
第8课时 解方程(1)
解:6.3+x-6.3=28.8-6.3
x=22.5
把x=22.5代入y-x=8,
得y-22.5=8
y-22.5+22.5=8+22.5
y=30.5
1.解方程,填一填。
(1) 5x=35
解:5x÷( )=35÷( )
x=( )
运用等式的性质2在方程的两边同时除以( ),就可以求出x的值。
第9课时 解方程(2)
5
5
7
5
(2) x÷40=3.2
解:x÷40×( )=3.2×( )
x=( )
运用等式的性质2在方程的两边同时乘( ),就可以求出x的值。
第9课时 解方程(2)
40
128
40
40
2.不计算,把下列每组方程中代表数值最大的字母圈出来。
第9课时 解方程(2)
3.解方程,带※的题要检验。
第9课时 解方程(2)
解:7.02x÷7.02=35.1÷7.02
x=5
解:x÷0.25×0.25=0.52×0.25
x=0.13
第9课时 解方程(2)
解:2.5x÷2.5=10÷2.5
x=4
检验:方程左边=2.5x
=2.5×4
=10
=方程右边
所以,x=4是方程的解。
4.根据题中的数量关系列出方程,并求出方程的解。
解:x÷5=50
x÷5×5=50×5
x=250
第9课时 解方程(2)
解:4x=7.2
4x÷4=7.2÷4
x=1.8
第9课时 解方程(2)
1.解方程,填一填。
第10课时 解方程(3)
x
16
x
0.2
第10课时 解方程(3)
x
15.6
x
28.4
3.解方程,带※的题要检验。
63-x=27
第10课时 解方程(3)
解:63-x+x=27+x
63=27+x
27+x=63
27+x-27=63-27
x=36
※12÷x=0.8
第10课时 解方程(3)
解:12÷x×x=0.8×x
12=0.8x
0.8x=12
0.8×x÷0.8=12÷0.8
x=15
检验:方程左边=12÷x
=12÷15
=12÷0.8
=方程右边
所以,x=15是方程的解。
4.把下面每个方程和它的解连起来。
第10课时 解方程(3)
5.a+b=61,a+c=71,b+c=62,求a+b+c的值。
61+71+62=194
194÷2=97
第10课时 解方程(3) 快乐导航
1.解方程,填一填。
6x-20=4
解:6x-20+20=4+( )
6x=( )
6x÷6=( )÷( )
x=( )
这是将( )看作一个整体,先求出( )的值,再求x的值。
第11课时 解方程(4)
20
24
24
6
4
6x
6x
(1)当 x =20 时,4x +5 ○ 82 ,4x -5 ○ 82 。
(2)当 x =0.8 时,3x +5x ○ 6.4 ,3x +5 ○ 6.4 。
(3)当 x =1.2 时, 5x -2 ○ 5 ,5x +2 ○ 5 。
2.在○里填上“>”“<”或“=”。
>
<
=
>
<
>
第11课时 解方程(4)
3.解方程,带 ※ 的题要检验。
4 x -18=48
第11课时 解方程(4)
解:4x-18+18=48+18
4x=66
4x÷4=66÷4
x=16.5
※ 2.2x +2.3×2=5.04
第11课时 解方程(4)
解:2.2x+4.6=5.04
2.2x+4.6-4.6=5.04-4.6
2.2x=0.44
2.2x÷2.2=0.44÷2.2
x=0.2
检验:方程左边=2.2x+2.3×2
=2.2×0.2+2.3×2
=0.44+4.6
=5.04
=方程右边
所以,x=0.2是方程的解。
4.看图列方程,并求解。
解:3x+90=300
3x+90-90=300-90
3x=210
3x÷3=210÷3
x=70
第11课时 解方程(4)
解:4x+22×2=68
4x+44=68
4x+44-44=68-44
4x=24
4x÷4=24÷4
x=6
第11课时 解方程(4)
0.6
40
40
5
35
x+5
x+5
1.解方程,填一填。
第12课时 解方程(5)
2.每课速算。
8.9a
3.6
4.3n
1.2
第12课时 解方程(5)
3.在○里填上“>”“<”或“=”。
(1)当x=8时,
(x+12)×6 ○ 120,x+12×6 ○ 120。
(2)当x=2.4时,
(x+12)÷5 ○ 0.8,(x-2)÷5 ○ 0.8
=
<
>
<
第12课时 解方程(5)
4.解方程并检验。
0.7(x+0.9)=42
第12课时 解方程(5)
解:0.7(x+0.9)÷0.7=42÷0.7
x+0.9=60
x+0.9-0.9=60-0.9
x=59.1
检验:
方程左边= 0.7(x+0.9)
=0.7×(59.1+0.9)
=0.7× 60
=42
=方程右边
所以,x=59.1是方程的解。
3(x÷4)=2.4
第12课时 解方程(5)
解:3(x÷4)÷3=2.4÷3
x÷4=0.8
x÷4×4=0.8×4
x=3.2
检验:
方程左边=3(x÷4)
=3×(3.2÷4)
=3×0.8
=2.4
=方程右边
所以,x=3.2是方程的解。
5.用方程表示下面的等量关系,并求出方程的解。
第12课时 解方程(5)
解:2(x+4.8)=12.8
2(x+4.8)÷2=12.8 ÷2
x+4.8=6.4
x+4.8-4.8=6.4-4.8
x=1.6
解:2x-6=92
2x-6+6=92+6
2x=98
2x ÷ 2=98 ÷ 2
x=49
1.根据题意,先补充完整数量间的等量关系,再列出方程。
妈妈买来一些牛奶,明明喝了12瓶,还剩8瓶,妈妈买来多少瓶牛奶?
解:设 。
(1)等量关系:
( )+( )=( )
方程:( )+( )=x
第13课时 实际问题与方程(1)
妈妈买来x瓶牛奶
喝了的牛奶
剩下的牛奶
买来的牛奶
12
8
(2)等量关系:
( )-( )=( )
方程:( )-( )=8
第13课时 实际问题与方程(1)
买来的牛奶
喝了的牛奶
剩下的牛奶
x
12
2.解方程。
x+6.7=18 x-8=18
第13课时 实际问题与方程(1)
解:x+6.7-6.7=18-6.7
x=11.3
解:x-8+8=18+8
x=26
3.先填空,再列方程解答。
(1)刘叔叔的身高是175 cm,文阿姨比刘叔叔矮11 cm,文阿姨的身高是多少厘米?
解:设______________________________ 。
等量关系: ______________________________
方程:
文阿姨的身高是x厘米
文阿姨的身高+11=刘叔叔的身高
x+11=175
x+11-11=175-11
x=164
第13课时 实际问题与方程(1)
(2) 明明买了4支圆珠笔花了18.4元,每支圆珠笔多少元?
解:设____________________________。
等量关系:____________________________
方程:
4x÷4=18.4÷4
x=4.6
第13课时 实际问题与方程(1)
每支圆珠笔x元
单价×数量=总价
4x=18.4
4.先写出等量关系,再列方程解答。
(1)五(1)班42名同学一共为希望工程捐款336元,平均每人捐款多少元?
解:设平均每人捐款x元。
42x=336
42x÷42=336÷42
x=8
答:平均每人捐款8元。
第13课时 实际问题与方程(1)
平均每人捐款的钱数×42=捐款总钱数
(2)一堆水泥运走13 t后,还剩27 t,这堆水泥原来有多少吨?
解:设这堆水泥原来有x t。
原来的吨数-运走的水泥吨数=剩下的吨数
x-13=27
x-13+13=27+13
x=40
答:这堆水泥原来有40 t。
第13课时 实际问题与方程(1)
1.根据题意,先补充完整数量间的等量关系,再列出方程。
妈妈买了3 kg苹果,她付了50元,找回3.5元,每千克苹果多少元?
解:设 ________________________。
(1)等量关系:
( )+( )=( )
方程:( )+( )=50
第14课时 实际问题与方程(2)
每千克苹果x元
苹果的总价
找回的钱数
付了的钱数
3x
3.5
(2)等量关系:
( )-( )=( )
方程:( )-( )=3x
(3)等量关系:
( )-( )=( )
方程:( )-( )=3.5
第14课时 实际问题与方程(2)
付了的钱数
找回的钱数
苹果的总价
50
3.5
付了的钱数
苹果的总价
找回的钱数
50
3x
2.先填空,再列方程解答。
(1)公园里种了100棵柳树,比松树的3倍多10棵。公园里种了松树多少棵?
解:设___________________。
等量关系:______________________________
方程:
公园里种了松树x棵
松树的棵数×3+10=柳树的棵数
3x+10=100
3x+10-10=100-10
3x=90
3x÷3=90÷3
x=30
答:公园里种了松树30棵。
第14课时 实际问题与方程(2)
(2)施工队修一条长1350 m的路,修了10天后,还剩下150 m没修,平均每天修多少米?
解:设___________________。
等量关系:_______________________________
方程:
平均每天修x m
已经修的长度+剩下的长度=要修的长度
10x+150=1350
10x+150-150=1350-150
10x=1200
10x÷10=1200÷10
x=120
答:平均每天修120m。
第14课时 实际问题与方程(2)
3.敏敏爸爸今年39岁,四年前敏敏爸爸的年龄是敏敏的7倍。敏敏今年多少岁?
第14课时 实际问题与方程(2)
解:设敏敏今年x岁。
四年前敏敏的年龄×7=四年前敏敏爸爸的年龄
7(x-4)=39-4
7(x-4)=35
7(x-4)÷7=35÷7
x-4=5
x-4+4=5+4
x=9
1.根据题意,先补充完整数量间的等量关系,再列出方程。
张老师买了铅笔和钢笔各10支,花了103元。每支铅笔1.8元,每支钢笔多少元?
解:设______________________________。
(1)等量关系:
__________+___________= _______________
方程:_______+____=103
第15课时 实际问题与方程(3)
每支钢笔x元
铅笔的总价
钢笔的总价
总价钱
1.8×10
10x
(2)等量关系:
_______________×10=_______________
方程:(_______)×10=103
第15课时 实际问题与方程(3)
两种笔的单价总和
总价钱
1.8+x
2.先填空,再列方程解答。
(1)甲、乙两个修路队共同修一条路,修了15天后,两队一共修了1800 m。甲队每天修65 m,乙队每天修多少米?
解:设______________。
等量关系:_______________________________
____________________________________________
乙队每天修x m
(甲队工作效率+乙队工作效率)×工作时间=工作总量
第15课时 实际问题与方程(3)
方程:
15(65+x)=1800
15(65+x)÷15=1800÷15
65+x=120
65+x-65=120-65
x=55
答:乙队每天修55 m。
第15课时 实际问题与方程(3)
(2)甲、乙两个修路队共同修一条路,修了15天后,甲队比乙队少修120 m。甲队每天修65 m,乙队每天修多少米?
解:设______________。
等量关系:_______________________________
_________________________________________
乙队每天修x m
(乙队工作效率-甲队工作效率)×工作时间=乙队工作总量-甲队工作总量
第15课时 实际问题与方程(3)
15(x-65)=120
15(x-65)÷15=120÷15
x-65=8
x-65+65=8+65
x=73
答:乙队每天修73 m。
方程:
3.辉辉到蛋糕店买了同样多的面包和蛋糕,花了24元,每个面包2.5元,每个蛋糕3.5元。辉辉买的面包和蛋糕各有多少个?
解:设辉辉买的面包和蛋糕各有x个。
(2.5+3.5)x=24
6x÷6=24÷6
x=4
答:辉辉买的面包和蛋糕各有4个。
第15课时 实际问题与方程(3)
1.根据题意,先补充完整数量间的等量关系,再列出方程。
养殖场饲养的母鸡数量是公鸡的8倍,母鸡和公鸡共有840只,该养殖场饲养的母鸡和公鸡各有多少只?
解:设_________________________。
等量关系:
( )+( )=( )
第16课时 实际问题与方程(4)
公鸡有x只,那么母鸡有8x只
公鸡的只数
母鸡的只数
总只数
方程:( )+( )=840
第16课时 实际问题与方程(4)
x
8x
2.解方程。
2x+0.4x=48 8x-2.6x=37.8
第16课时 实际问题与方程(4)
解:2.4x=48
2.4x ÷ 2.4=48 ÷ 2.4
x=20
解:5.4x=37.8
5.4x ÷ 5.4=37.8 ÷ 5.4
x=7
3.看图列方程,并求出方程的解。
解:x+5x=150
6x=150
6x÷6=150÷6
x=25
解:3x-x=21.4
2x=21.4
2x ÷ 2=21.4 ÷ 2
x=10.7
第16课时 实际问题与方程(4)
4.数量相同的鸡、兔同笼,鸡和兔的脚共有48只。鸡和兔各有多少只?(用方程解答)
解:设鸡和兔各有x只。
(2+4)x=48
6x=48
6x÷6=48÷6
x=8
答:鸡和兔各有8只。
第16课时 实际问题与方程(4)
1.甲、乙两车同时从两地出发,相向而行。经过几小时两车相遇?
解:设______________________。
(1)等量关系:__________ +__________=_______
方程:______+ ______=350
第17课时 实际问题与方程(5)
经过x 小时两车相遇
甲车的路程
总路程
乙车的路程
55x
45x
(2)等量关系:
(_____________________)×___________=_______
方程:(______)×______=350
第17课时 实际问题与方程(5)
甲车的速度+乙车的速度
相遇的时间
总路程
55+45
x
2.解方程。
9.1÷x=0.7 4.6+4x=5.6
第17课时 实际问题与方程(5)
解: 9.1÷x×x = 0.7×x
9.1= 0.7x
0.7x= 9.1
0.7x÷ 0.7 = 9.1÷ 0.7
x= 13
解: 4.6+4x-4.6 = 5.6-4.6
4x = 1
4x÷ 4 = 1÷ 4
x = 0.25
3.水果批发市场要运进35t苹果,平均每次运3.5t 。上午运了 6 次,下午还要运多少次才能运完?
第17课时 实际问题与方程(5)
解: 设下午还要运x次才能运完。
3.5(6+x) = 35
3.5(6+x)÷3.5 = 35 ÷ 3.5
6+x= 10
6+x-6= 10-6
x = 4
4.甲车每小时行40 km,乙车每小时行50 km。甲、乙两车分别从A、B两地同时出发相向而行,相遇后甲车又用了3小时到达B地。A、B两地相距多少千米?
第17课时 实际问题与方程(5)
第17课时 实际问题与方程(5)
解:设甲、乙两车经过x小时相遇。
50x = 40×3
50x = 120
50x÷50 = 120÷50
x = 2.4
(40+50)×2.4
= 90×2.4
= 216(km)
答:A、B两地相距216km。
1.省略乘号写出下面的算式。
a×16= t×t=
a×b= 5×h=
第18课时 整理和复习
16a
t2
ab
5h
2.解下列方程。
2.5x+3x=11 3.1x-2=4.51
第18课时 整理和复习
解:5.5x = 11
5.5x÷5.5 = 11÷ 5.5
x = 2
解:3.1x-2+2 = 4.51-2+2
3.1x = 6.51
3.1x÷3.1 = 6.51÷ 3.1
x = 2.1
7(x-1.2)= 2.1
第18课时 整理和复习
解:7(x-1.2)÷7 = 2.1 ÷7
x-1.2 = 0.3
x-1.2+1.2 = 0.3+1.2
x = 1.5
3.写出下列各题中的等量关系,再把方程补充完整。
(1)某工地一共需要180t水泥,派出8辆车来运,平均每辆车运x t。
等量关系:_______________________________
方程:( )=180
第18课时 整理和复习
每辆车运的吨数×8=需要运的水泥吨数
8x
(2)祥祥买了2千克橘子,每千克x元,她付给售货员50元,找回29元。
等量关系:_______________________________
方程:( )=29
第18课时 整理和复习
付的钱数-橘子的总价=找回的钱数
50-2x
4.妈妈买了苹果和梨各3千克,一共花了56.1元。苹果每千克10元,梨每千克多少元?
解:设梨每千克x元。
(10+x)×3= 56.1
(10+x)×3÷3= 56.1÷3
10+x= 18.7
10+x-10 = 18.7-10
x = 8.7
答:梨每千克8.7元。
第18课时 整理和复习
5.
小佩和小艺各有邮票多少张
第18课时 整理和复习
解:设小艺有x张邮票,那么小佩有3x张。
x+5=3x-5
x+5-x=3x-5-x
5=2x-5
2x-5=5
2x-5+5=5+5
2x=10
2x÷2=10÷2
x=5
3x
=3×5
=15
答:小艺有5张邮票,小佩有15张邮票。
第18课时 整理和复习
5 简易方程
数学配人教版
(五年级/上册)
第1课时 用字母表示数(1)
第2课时 用字母表示数(2)
第3课时 用字母表示数(3)
第4课时 用字母表示数(4)
第5课时 用字母表示数(5)
第6课时 方程的意义
第7课时 等式的性质
第8课时 解方程(1)
第9课时 解方程(2)
第10课时 解方程(3)
第11课时 解方程(4)
第12课时 解方程(5)
第13课时 实际问题与方程(1)
第14课时 实际问题与方程(2)
第15课时 实际问题与方程(3)
第16课时 实际问题与方程(4)
第17课时 实际问题与方程(5)
第18课时 整理和复习
胡萝卜的价格/ (元/千克) 2 3.4 5 x
白菜的价格/ (元/千克)
1.填表。(每千克白菜比胡萝卜便宜0.8元)
第1课时 用字母表示数(1)
1.2
2.6
4.2
x-0.8
0.48÷0.16= 0.4×3.5×2=
0.45×0.6= 15÷1.5=
1.36÷0.4= 0.8+0.8÷4=
2.每课速算。
第1课时 用字母表示数(1)
3
2.8
0.27
10
3.4
1
3.填空题。
(1)某水库的水位高度为h m,水位上升2 m后的高度为( )m。
(2)学校图书馆计划购进图书a本,实际比计划多购进b本,实际购进图书( )本。
第1课时 用字母表示数(1)
h+2
a+b
(3)手套每双16.8元,帽子每顶m元,围巾每条n元。
①买一双手套和一顶帽子花费( )元。
②一双手套比一条围巾便宜( )元。
(4)五(1)班有a人,五(2)班有b人。
①a-b表示( )。
②a÷b表示( )。
五(1)班比五(2)班多多少人
五(1)班的人数是五(2)班的多少倍
第1课时 用字母表示数(1)
n-16.8
16.8+m
4.五(1)班有男生x人,女生比男生少5人。
(1)用含有字母的式子表示五(1)班女生的人数、全班的人数。
女生的人数:x-5
全班的人数:2x-5
第1课时 用字母表示数(1)
(2)当x=23时,五(1)班女生有多少人?全班有多少人?
当x=23时,
x-5
=23-5
=18
2x-5
=23×2-5
=46-5
=41
答:五(1)班女生有18人,全班有41人。
第1课时 用字母表示数(1)
5.一辆公共汽车上原有16个人,到站后下去m人,又上来n人。
(1)用含有字母的式子表示现在车上有多少人。
16-m+n
第1课时 用字母表示数(1)
(2)当m=5,n=7时,现在车上有多少人?
当m=5,n=7时,
16-m+n
=16-5+7
=11+7
=18
答:现在车上有18人。
第1课时 用字母表示数(1)
第2课时 用字母表示数(2)
5.6
16.8
19.6
32.48
5.6x
2.省略乘号,写出下列算式。
x×30= a×b=
1×d= x×8.2 × y=
第2课时 用字母表示数(2)
30x
8.2xy
ab
d
3.填空题。
(1)小莉每天练20个大字,m天练( )个大字。
(2)书店卖出30本童话书,一共卖了a元,每本童话书的售价是( )元。
(3)一种花布每米25.6元,买x m这样的花布应付( )元
第2课时 用字母表示数(2)
20m
a÷30
25.6x
(4)有x名同学,平均分成6组,每组有( )名同学。
(5)商店卖出21台手机,每台手机的售价是x元,商店一共卖了( )元。
第2课时 用字母表示数(2)
x÷6
21x
4.判断题。(对的画“√”,错的画“×”)
(1)x+x+x+x+x=5x( )
(2)x×7=7x( )
(3)x÷2=2x( )
第2课时 用字母表示数(2)
√
×
√
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(1)苹果共有多少千克?
用字母写出数量关系式:_______________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
ac
当a = 15,c =5时,
ac = 15×5
= 75
答:苹果共有75kg。
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(2)每箱苹果比桃轻多少千克?
用字母写出数量关系式:_____________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
d-c
当c = 5,d = 6时,
d-c
= 6-5
= 1
答:每箱苹果比桃轻1kg。
5.水果店运来a箱苹果,b箱桃,每箱苹果的质量是c kg,每箱桃的质量是d kg。a=15,b=12,c=5,d=6。
(3)苹果和桃共有多少箱?
用字母写出数量关系式:____________。
把题中的数代入含有字母的式子,并计算。
第2课时 用字母表示数(2)
a+b
当a = 15,b = 12时,
a+b
= 15+12
= 27
答:苹果和桃共有27箱。
6.不同的汉字代表不同的数字,请你算出下面这些汉字所代表的数字。
1
2
3
第2课时 用字母表示数(2)
1.用字母表示下面图形的周长和面积的计算公式。
第3课时 用字母表示数(3)
C = 2(a+b)
S = ab
C = 4a
S = a2
2.根据运算定律填上适当的数或字母。
(1)a+_____=6+ _____
(2)m+(n+8)=( + )+8
(3)4×x+6×x=( + )×
6
a
m
n
4
6
x
第3课时 用字母表示数(3)
3.把结果相同的算式用线连起来。
第3课时 用字母表示数(3)
4.a表示工作效率,t表示工作时间,c表示工作总量。
(1)用字母表示出它们的数量关系。
c=( )
a=( )
t=( )
at
c÷t
c÷a
第3课时 用字母表示数(3)
(2)张师傅3小时加工240个零件,利用(1)中的公式计算他每小时加工多少个零件。
当t = 3,c = 240时,
a = c÷t
= 240÷3
= 80
答:他每小时加工80个零件。
第3课时 用字母表示数(3)
5.v表示速度,t表示时间,s表示路程。
(1)用字母表示出它们的数量关系。
s=( )
v=( )
t=( )
vt
s÷t
s÷v
第3课时 用字母表示数(3)
(2)一辆汽车每小时行驶56 km,行驶168 km需要多少小时?利用上面的公式计算。
当v = 56,s = 168时,
t = s÷v
= 168÷56
= 3
答:行驶168km需要3小时。
第3课时 用字母表示数(3)
6.a表示单价,x表示数量,c表示总价。
(1)用字母表示出它们的数量关系。
c=( )
a=( )
x=( )
ax
c÷x
c÷a
第3课时 用字母表示数(3)
(2)一盒牛奶5.8元,小明要买6盒,需要花多少钱?利用上面的公式计算。
第3课时 用字母表示数(3)
当a = 5.8,x = 6时,
c = ax
=5.8×6
=34.8
答:需要花34.8元。
7.用含有字母的式子表示下图中阴影部分的面积。
a2+b2
第3课时 用字母表示数(3)
1.用含有字母的式子表示下面的数量关系。
(1)x与8的和。 ( )
(2)比b大8.6的数。 ( )
(3)x 与y的差除以6。 ( )
(4)t的平方加上 12。 ( )
(5)比a 的7倍少3。 ( )
(6)m除以9的商。 ( )
第4课时 用字母表示数(4)
x+8
b+8.6
(x-y)÷ 6
t2+12
7a-3
m ÷ 9
2.每课速算。
0.5
第4课时 用字母表示数(4)
0.2
4
22
3.(1)当x=6.5,y =15.3时,求x +y的值。
(2)当m=45,n=12时,求(m-n)÷3的值
当x= 6.5,y = 15.3时,
x+y
= 6.5+15.3
= 21.8
第4课时 用字母表示数(4)
当m = 45,n = 12时,
(m-n)÷3
= (45-12)÷3
= 33÷3
= 11
4.钢笔每支a元,铅笔每支b元。
(1)买2支钢笔和5支铅笔共需要花 元。
(2)当a=8,b=2时,买2支钢笔和5支铅笔共需要花多少钱?
第4课时 用字母表示数(4)
2a+5b
当a=8,b=2时,
2a+5b
=2×8+5×2
=16+10
=26
答:买2支钢笔和5支铅笔共需要花26元。
5.水果店原来有60 kg苹果,又运来16箱苹果,每箱重x kg。
(1)用式子表示水果店现在有多少千克苹果。
(2)当x=8时,水果店一共有多少千克苹果?
60+16x
当x=8时,
60+16x
=60+16×8
=60+128
=188
答:水果店一共有188 kg苹果。
第4课时 用字母表示数(4)
6.当x=4时,x2和3x各等于多少?当x的值是多少时,x2和3x相等?
第4课时 用字母表示数(4)
第4课时 用字母表示数(4)
当x=4时,
x2 =4×4
= 16
3x =3×4
=12
当x=0或x=3时,x2=3x
答:当x=4时,x2 等于16,3x 等于12。
当x= 0或x=3时,x2 和3x 相等。
1.用小棒摆图形。
(1)摆x个正方形和x个长方形,一共要用多少根小棒?
第5课时 用字母表示数(5)
4x+6x = 10x
答:一共要用10x根小棒。
(2)当x=10时,一共要用多少根小棒?
第5课时 用字母表示数(5)
当x = 10时,
10x = 10×10
= 100
答:一共要用100根小棒。
2.客车的速度是65千米/时,货车的速度是55千米/时。
(1)行驶t小时,两车一共行驶多少千米?当t=5时,两车一共行驶多少千米?
65t+55t = 120t
当t = 5时,
120t =120×5
= 600
答:行驶t小时,两车一共行驶120t km,当t=5时,两车一共行驶600km。
第5课时 用字母表示数(5)
(2)行驶t小时,客车比货车多行驶多少千米?当t=4时,客车比货车多行驶多少千米?
65t-55t = 10t
当t = 4时,
10t = 10×4
= 40
答:行驶t小时,客车比货车多行驶10t km,当t=4 时,客车比货车多行驶 40km。
第5课时 用字母表示数(5)
3.筑路队铺一条长400 km的公路,已经铺了15天,每天铺a km。
(1)用式子表示已经铺了多少千米。当a=2时,已经铺了多少千米?
15a
当a = 2时,
15a
= 15×2
= 30
第5课时 用字母表示数(5)
答:已经铺了15a km,当a=2时,已经铺了30km。
(2)用式子表示还剩多少千米没铺。当a=3时,还剩多少千米没铺?
400-15a
当a = 3时,
400-15a
= 400-15×3
= 400-45
= 355
答:还剩(400-15a)km没铺,当a=3时,还剩355km没铺。
第5课时 用字母表示数(5)
4.
(1)像这样摆下去,摆n个六边形需要( )根小棒。
1+5n
第5课时 用字母表示数(5)
4.
(2)当n=20时,用第(1)题的式子计算摆20个六边形需要的小棒数。
当n = 20时,
1+5n
= 1+5×20
= 1+100
= 101
第5课时 用字母表示数(5)
答:摆20个六边形需要101根小棒。
1.下面哪些式子是方程?在方程后面的括号里画“√”。
2×9=3×6 ( ) 6+9<3×9 ( )
3x>7+5 ( ) 5y=30-x ( )
a ÷ 0.8=32 ( ) 6m+8 ( )
第6课时 方程的意义
√
√
2.每课速算。
第6课时 方程的意义
3a
13
0.4x
25
0.08b
0.185
11x
0.16
3.判断题。(对的画“√”,错的画“×”)
(1)含有未知数的式子叫作方程。 ( )
(2)5x+1是方程。 ( )
(3)a2一定大于2a。( )
(4)4+8=3y是方程。( )
第6课时 方程的意义
×
×
×
√
4.用方程表示下面的数量关系。
第6课时 方程的意义
5.用方程表示下面数量之间的关系。
(1)有x张书签,平均分给6个小朋友,每个人分到3张。
(2)摩托车每分钟行800 m,x分钟行了2800 m。
第6课时 方程的意义
(3)小菲的体重是a kg,妹妹的体重是36 kg,两人的体重一共是80 kg。
(4)父亲今年n岁,比儿子大28岁,儿子今年6岁。
第6课时 方程的意义
(5)公共汽车上原来有9名乘客,到站后有x名乘客下车,有5名乘客上车,现在车上有12名乘客。
第6课时 方程的意义
1.看图填空。
1个西瓜和( )个石榴的质量相等,两边各放上1个石榴,天平保持平衡。天平两边再各去掉1个石榴,天平仍保持( )。
第7课时 等式的性质
2
平衡
平衡的天平两边的物品质量都扩大到原来的( )倍,天平仍然保持( )。平衡的天平两边的物品质量都缩小到原来的( ),天平仍然保持( )。
第7课时 等式的性质
2
平衡
平衡
2.每课速算。
5.6x
第7课时 等式的性质
1.2
1.18y
0.1
0.01
4m
0.018
3.2x
3.在○里填上适当的运算符号,在括号里填上适当的数,使天平平衡。
第7课时 等式的性质
+ 60
- 20
× 9
÷ 3
第7课时 等式的性质
4.根据等式的性质填空。
(1)x+8=36
x+8-( )=36-8
(2)x-9=43
x-9+( )=43+9
(3)3x=1.2
3x÷( )=1.2÷3
(4)x÷1.5=3.7
x÷1.5×( )=3.7×1.5
8
9
3
1.5
第7课时 等式的性质
5.如果x = y,根据等式的性质填空。
x-3= y-( )
x÷( )= y÷10
3
10
第7课时 等式的性质
6.已知 ○+○+○+○=△+○+○,那么△=( )个○。
2
第7课时 等式的性质
1.解方程,填一填。
第8课时 解方程(1)
2.5
11.3
2.5
2.5
第8课时 解方程(1)
3.6
3.6
15.7
3.6
2.后面括号中哪个x的值是方程的解?请在正确的解上画“√”。
第8课时 解方程(1)
√
√
√
√
3.解方程,带※的题要检验。
125+x=164 x+8.05=10.2
第8课时 解方程(1)快乐导航
解:125+x-125=164-125
x=39
解:x+8.05-8.05=10.2-8.05
x=2.15
※x-15=1.5
第8课时 解方程(1)
解:x-1.5+1.5=1.5+1.5
x=3
检验: 方程左边=x-1.5
=3-1.5
=1.5
=方程右边
所 以,x=3是方程的解。
4.根据题中的数量关系列出方程,并求出方程的解。
第8课时 解方程(1)
解:x-5= 26
x-5+5=26+5
x=31
解:x+4.8=8.2
x+4.8-4.8=8.2-4.8
x=3.4
5.方程方程6.3+x=28. 8与y-x =8的x的值相同,求 y 的值。
第8课时 解方程(1)
第8课时 解方程(1)
解:6.3+x-6.3=28.8-6.3
x=22.5
把x=22.5代入y-x=8,
得y-22.5=8
y-22.5+22.5=8+22.5
y=30.5
1.解方程,填一填。
(1) 5x=35
解:5x÷( )=35÷( )
x=( )
运用等式的性质2在方程的两边同时除以( ),就可以求出x的值。
第9课时 解方程(2)
5
5
7
5
(2) x÷40=3.2
解:x÷40×( )=3.2×( )
x=( )
运用等式的性质2在方程的两边同时乘( ),就可以求出x的值。
第9课时 解方程(2)
40
128
40
40
2.不计算,把下列每组方程中代表数值最大的字母圈出来。
第9课时 解方程(2)
3.解方程,带※的题要检验。
第9课时 解方程(2)
解:7.02x÷7.02=35.1÷7.02
x=5
解:x÷0.25×0.25=0.52×0.25
x=0.13
第9课时 解方程(2)
解:2.5x÷2.5=10÷2.5
x=4
检验:方程左边=2.5x
=2.5×4
=10
=方程右边
所以,x=4是方程的解。
4.根据题中的数量关系列出方程,并求出方程的解。
解:x÷5=50
x÷5×5=50×5
x=250
第9课时 解方程(2)
解:4x=7.2
4x÷4=7.2÷4
x=1.8
第9课时 解方程(2)
1.解方程,填一填。
第10课时 解方程(3)
x
16
x
0.2
第10课时 解方程(3)
x
15.6
x
28.4
3.解方程,带※的题要检验。
63-x=27
第10课时 解方程(3)
解:63-x+x=27+x
63=27+x
27+x=63
27+x-27=63-27
x=36
※12÷x=0.8
第10课时 解方程(3)
解:12÷x×x=0.8×x
12=0.8x
0.8x=12
0.8×x÷0.8=12÷0.8
x=15
检验:方程左边=12÷x
=12÷15
=12÷0.8
=方程右边
所以,x=15是方程的解。
4.把下面每个方程和它的解连起来。
第10课时 解方程(3)
5.a+b=61,a+c=71,b+c=62,求a+b+c的值。
61+71+62=194
194÷2=97
第10课时 解方程(3) 快乐导航
1.解方程,填一填。
6x-20=4
解:6x-20+20=4+( )
6x=( )
6x÷6=( )÷( )
x=( )
这是将( )看作一个整体,先求出( )的值,再求x的值。
第11课时 解方程(4)
20
24
24
6
4
6x
6x
(1)当 x =20 时,4x +5 ○ 82 ,4x -5 ○ 82 。
(2)当 x =0.8 时,3x +5x ○ 6.4 ,3x +5 ○ 6.4 。
(3)当 x =1.2 时, 5x -2 ○ 5 ,5x +2 ○ 5 。
2.在○里填上“>”“<”或“=”。
>
<
=
>
<
>
第11课时 解方程(4)
3.解方程,带 ※ 的题要检验。
4 x -18=48
第11课时 解方程(4)
解:4x-18+18=48+18
4x=66
4x÷4=66÷4
x=16.5
※ 2.2x +2.3×2=5.04
第11课时 解方程(4)
解:2.2x+4.6=5.04
2.2x+4.6-4.6=5.04-4.6
2.2x=0.44
2.2x÷2.2=0.44÷2.2
x=0.2
检验:方程左边=2.2x+2.3×2
=2.2×0.2+2.3×2
=0.44+4.6
=5.04
=方程右边
所以,x=0.2是方程的解。
4.看图列方程,并求解。
解:3x+90=300
3x+90-90=300-90
3x=210
3x÷3=210÷3
x=70
第11课时 解方程(4)
解:4x+22×2=68
4x+44=68
4x+44-44=68-44
4x=24
4x÷4=24÷4
x=6
第11课时 解方程(4)
0.6
40
40
5
35
x+5
x+5
1.解方程,填一填。
第12课时 解方程(5)
2.每课速算。
8.9a
3.6
4.3n
1.2
第12课时 解方程(5)
3.在○里填上“>”“<”或“=”。
(1)当x=8时,
(x+12)×6 ○ 120,x+12×6 ○ 120。
(2)当x=2.4时,
(x+12)÷5 ○ 0.8,(x-2)÷5 ○ 0.8
=
<
>
<
第12课时 解方程(5)
4.解方程并检验。
0.7(x+0.9)=42
第12课时 解方程(5)
解:0.7(x+0.9)÷0.7=42÷0.7
x+0.9=60
x+0.9-0.9=60-0.9
x=59.1
检验:
方程左边= 0.7(x+0.9)
=0.7×(59.1+0.9)
=0.7× 60
=42
=方程右边
所以,x=59.1是方程的解。
3(x÷4)=2.4
第12课时 解方程(5)
解:3(x÷4)÷3=2.4÷3
x÷4=0.8
x÷4×4=0.8×4
x=3.2
检验:
方程左边=3(x÷4)
=3×(3.2÷4)
=3×0.8
=2.4
=方程右边
所以,x=3.2是方程的解。
5.用方程表示下面的等量关系,并求出方程的解。
第12课时 解方程(5)
解:2(x+4.8)=12.8
2(x+4.8)÷2=12.8 ÷2
x+4.8=6.4
x+4.8-4.8=6.4-4.8
x=1.6
解:2x-6=92
2x-6+6=92+6
2x=98
2x ÷ 2=98 ÷ 2
x=49
1.根据题意,先补充完整数量间的等量关系,再列出方程。
妈妈买来一些牛奶,明明喝了12瓶,还剩8瓶,妈妈买来多少瓶牛奶?
解:设 。
(1)等量关系:
( )+( )=( )
方程:( )+( )=x
第13课时 实际问题与方程(1)
妈妈买来x瓶牛奶
喝了的牛奶
剩下的牛奶
买来的牛奶
12
8
(2)等量关系:
( )-( )=( )
方程:( )-( )=8
第13课时 实际问题与方程(1)
买来的牛奶
喝了的牛奶
剩下的牛奶
x
12
2.解方程。
x+6.7=18 x-8=18
第13课时 实际问题与方程(1)
解:x+6.7-6.7=18-6.7
x=11.3
解:x-8+8=18+8
x=26
3.先填空,再列方程解答。
(1)刘叔叔的身高是175 cm,文阿姨比刘叔叔矮11 cm,文阿姨的身高是多少厘米?
解:设______________________________ 。
等量关系: ______________________________
方程:
文阿姨的身高是x厘米
文阿姨的身高+11=刘叔叔的身高
x+11=175
x+11-11=175-11
x=164
第13课时 实际问题与方程(1)
(2) 明明买了4支圆珠笔花了18.4元,每支圆珠笔多少元?
解:设____________________________。
等量关系:____________________________
方程:
4x÷4=18.4÷4
x=4.6
第13课时 实际问题与方程(1)
每支圆珠笔x元
单价×数量=总价
4x=18.4
4.先写出等量关系,再列方程解答。
(1)五(1)班42名同学一共为希望工程捐款336元,平均每人捐款多少元?
解:设平均每人捐款x元。
42x=336
42x÷42=336÷42
x=8
答:平均每人捐款8元。
第13课时 实际问题与方程(1)
平均每人捐款的钱数×42=捐款总钱数
(2)一堆水泥运走13 t后,还剩27 t,这堆水泥原来有多少吨?
解:设这堆水泥原来有x t。
原来的吨数-运走的水泥吨数=剩下的吨数
x-13=27
x-13+13=27+13
x=40
答:这堆水泥原来有40 t。
第13课时 实际问题与方程(1)
1.根据题意,先补充完整数量间的等量关系,再列出方程。
妈妈买了3 kg苹果,她付了50元,找回3.5元,每千克苹果多少元?
解:设 ________________________。
(1)等量关系:
( )+( )=( )
方程:( )+( )=50
第14课时 实际问题与方程(2)
每千克苹果x元
苹果的总价
找回的钱数
付了的钱数
3x
3.5
(2)等量关系:
( )-( )=( )
方程:( )-( )=3x
(3)等量关系:
( )-( )=( )
方程:( )-( )=3.5
第14课时 实际问题与方程(2)
付了的钱数
找回的钱数
苹果的总价
50
3.5
付了的钱数
苹果的总价
找回的钱数
50
3x
2.先填空,再列方程解答。
(1)公园里种了100棵柳树,比松树的3倍多10棵。公园里种了松树多少棵?
解:设___________________。
等量关系:______________________________
方程:
公园里种了松树x棵
松树的棵数×3+10=柳树的棵数
3x+10=100
3x+10-10=100-10
3x=90
3x÷3=90÷3
x=30
答:公园里种了松树30棵。
第14课时 实际问题与方程(2)
(2)施工队修一条长1350 m的路,修了10天后,还剩下150 m没修,平均每天修多少米?
解:设___________________。
等量关系:_______________________________
方程:
平均每天修x m
已经修的长度+剩下的长度=要修的长度
10x+150=1350
10x+150-150=1350-150
10x=1200
10x÷10=1200÷10
x=120
答:平均每天修120m。
第14课时 实际问题与方程(2)
3.敏敏爸爸今年39岁,四年前敏敏爸爸的年龄是敏敏的7倍。敏敏今年多少岁?
第14课时 实际问题与方程(2)
解:设敏敏今年x岁。
四年前敏敏的年龄×7=四年前敏敏爸爸的年龄
7(x-4)=39-4
7(x-4)=35
7(x-4)÷7=35÷7
x-4=5
x-4+4=5+4
x=9
1.根据题意,先补充完整数量间的等量关系,再列出方程。
张老师买了铅笔和钢笔各10支,花了103元。每支铅笔1.8元,每支钢笔多少元?
解:设______________________________。
(1)等量关系:
__________+___________= _______________
方程:_______+____=103
第15课时 实际问题与方程(3)
每支钢笔x元
铅笔的总价
钢笔的总价
总价钱
1.8×10
10x
(2)等量关系:
_______________×10=_______________
方程:(_______)×10=103
第15课时 实际问题与方程(3)
两种笔的单价总和
总价钱
1.8+x
2.先填空,再列方程解答。
(1)甲、乙两个修路队共同修一条路,修了15天后,两队一共修了1800 m。甲队每天修65 m,乙队每天修多少米?
解:设______________。
等量关系:_______________________________
____________________________________________
乙队每天修x m
(甲队工作效率+乙队工作效率)×工作时间=工作总量
第15课时 实际问题与方程(3)
方程:
15(65+x)=1800
15(65+x)÷15=1800÷15
65+x=120
65+x-65=120-65
x=55
答:乙队每天修55 m。
第15课时 实际问题与方程(3)
(2)甲、乙两个修路队共同修一条路,修了15天后,甲队比乙队少修120 m。甲队每天修65 m,乙队每天修多少米?
解:设______________。
等量关系:_______________________________
_________________________________________
乙队每天修x m
(乙队工作效率-甲队工作效率)×工作时间=乙队工作总量-甲队工作总量
第15课时 实际问题与方程(3)
15(x-65)=120
15(x-65)÷15=120÷15
x-65=8
x-65+65=8+65
x=73
答:乙队每天修73 m。
方程:
3.辉辉到蛋糕店买了同样多的面包和蛋糕,花了24元,每个面包2.5元,每个蛋糕3.5元。辉辉买的面包和蛋糕各有多少个?
解:设辉辉买的面包和蛋糕各有x个。
(2.5+3.5)x=24
6x÷6=24÷6
x=4
答:辉辉买的面包和蛋糕各有4个。
第15课时 实际问题与方程(3)
1.根据题意,先补充完整数量间的等量关系,再列出方程。
养殖场饲养的母鸡数量是公鸡的8倍,母鸡和公鸡共有840只,该养殖场饲养的母鸡和公鸡各有多少只?
解:设_________________________。
等量关系:
( )+( )=( )
第16课时 实际问题与方程(4)
公鸡有x只,那么母鸡有8x只
公鸡的只数
母鸡的只数
总只数
方程:( )+( )=840
第16课时 实际问题与方程(4)
x
8x
2.解方程。
2x+0.4x=48 8x-2.6x=37.8
第16课时 实际问题与方程(4)
解:2.4x=48
2.4x ÷ 2.4=48 ÷ 2.4
x=20
解:5.4x=37.8
5.4x ÷ 5.4=37.8 ÷ 5.4
x=7
3.看图列方程,并求出方程的解。
解:x+5x=150
6x=150
6x÷6=150÷6
x=25
解:3x-x=21.4
2x=21.4
2x ÷ 2=21.4 ÷ 2
x=10.7
第16课时 实际问题与方程(4)
4.数量相同的鸡、兔同笼,鸡和兔的脚共有48只。鸡和兔各有多少只?(用方程解答)
解:设鸡和兔各有x只。
(2+4)x=48
6x=48
6x÷6=48÷6
x=8
答:鸡和兔各有8只。
第16课时 实际问题与方程(4)
1.甲、乙两车同时从两地出发,相向而行。经过几小时两车相遇?
解:设______________________。
(1)等量关系:__________ +__________=_______
方程:______+ ______=350
第17课时 实际问题与方程(5)
经过x 小时两车相遇
甲车的路程
总路程
乙车的路程
55x
45x
(2)等量关系:
(_____________________)×___________=_______
方程:(______)×______=350
第17课时 实际问题与方程(5)
甲车的速度+乙车的速度
相遇的时间
总路程
55+45
x
2.解方程。
9.1÷x=0.7 4.6+4x=5.6
第17课时 实际问题与方程(5)
解: 9.1÷x×x = 0.7×x
9.1= 0.7x
0.7x= 9.1
0.7x÷ 0.7 = 9.1÷ 0.7
x= 13
解: 4.6+4x-4.6 = 5.6-4.6
4x = 1
4x÷ 4 = 1÷ 4
x = 0.25
3.水果批发市场要运进35t苹果,平均每次运3.5t 。上午运了 6 次,下午还要运多少次才能运完?
第17课时 实际问题与方程(5)
解: 设下午还要运x次才能运完。
3.5(6+x) = 35
3.5(6+x)÷3.5 = 35 ÷ 3.5
6+x= 10
6+x-6= 10-6
x = 4
4.甲车每小时行40 km,乙车每小时行50 km。甲、乙两车分别从A、B两地同时出发相向而行,相遇后甲车又用了3小时到达B地。A、B两地相距多少千米?
第17课时 实际问题与方程(5)
第17课时 实际问题与方程(5)
解:设甲、乙两车经过x小时相遇。
50x = 40×3
50x = 120
50x÷50 = 120÷50
x = 2.4
(40+50)×2.4
= 90×2.4
= 216(km)
答:A、B两地相距216km。
1.省略乘号写出下面的算式。
a×16= t×t=
a×b= 5×h=
第18课时 整理和复习
16a
t2
ab
5h
2.解下列方程。
2.5x+3x=11 3.1x-2=4.51
第18课时 整理和复习
解:5.5x = 11
5.5x÷5.5 = 11÷ 5.5
x = 2
解:3.1x-2+2 = 4.51-2+2
3.1x = 6.51
3.1x÷3.1 = 6.51÷ 3.1
x = 2.1
7(x-1.2)= 2.1
第18课时 整理和复习
解:7(x-1.2)÷7 = 2.1 ÷7
x-1.2 = 0.3
x-1.2+1.2 = 0.3+1.2
x = 1.5
3.写出下列各题中的等量关系,再把方程补充完整。
(1)某工地一共需要180t水泥,派出8辆车来运,平均每辆车运x t。
等量关系:_______________________________
方程:( )=180
第18课时 整理和复习
每辆车运的吨数×8=需要运的水泥吨数
8x
(2)祥祥买了2千克橘子,每千克x元,她付给售货员50元,找回29元。
等量关系:_______________________________
方程:( )=29
第18课时 整理和复习
付的钱数-橘子的总价=找回的钱数
50-2x
4.妈妈买了苹果和梨各3千克,一共花了56.1元。苹果每千克10元,梨每千克多少元?
解:设梨每千克x元。
(10+x)×3= 56.1
(10+x)×3÷3= 56.1÷3
10+x= 18.7
10+x-10 = 18.7-10
x = 8.7
答:梨每千克8.7元。
第18课时 整理和复习
5.
小佩和小艺各有邮票多少张
第18课时 整理和复习
解:设小艺有x张邮票,那么小佩有3x张。
x+5=3x-5
x+5-x=3x-5-x
5=2x-5
2x-5=5
2x-5+5=5+5
2x=10
2x÷2=10÷2
x=5
3x
=3×5
=15
答:小艺有5张邮票,小佩有15张邮票。
第18课时 整理和复习
