7.5正态分布 课件(共23张PPT)
文档属性
| 名称 | 7.5正态分布 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
正态分布
这个计算非常困难,
有没有其他计算呢方法呢?
X 0 1 2 3 4 5 6
P
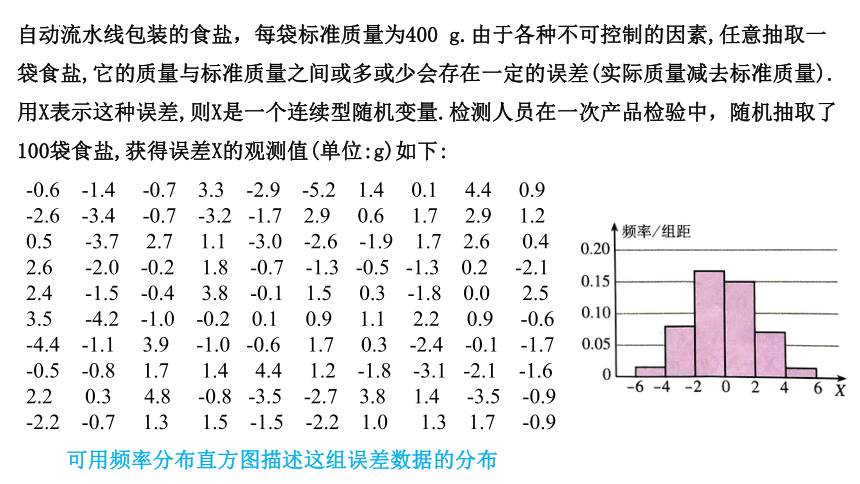
自动流水线包装的食盐,每袋标准质量为400 g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X的观测值(单位:g)如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
可用频率分布直方图描述这组误差数据的分布
正态分布又称为高斯分布
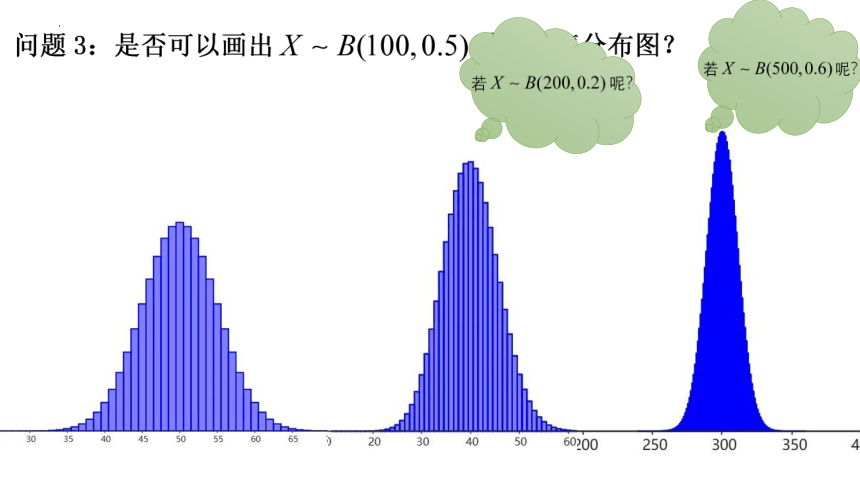
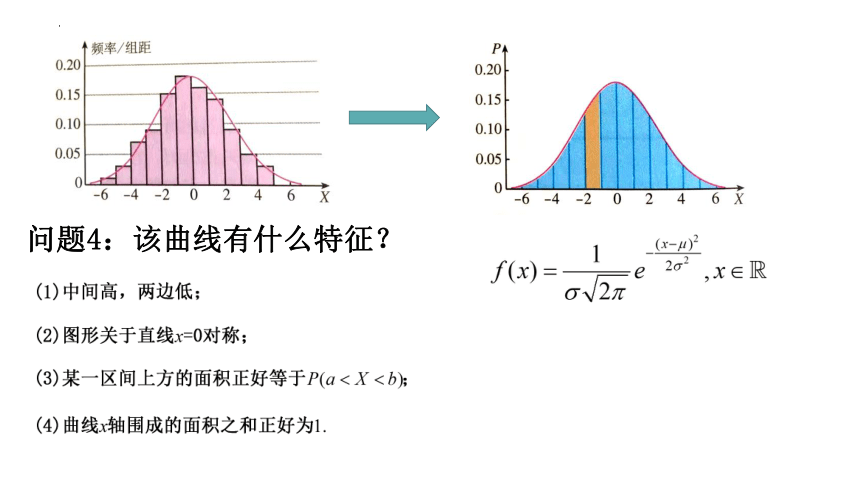
问题5:观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点?
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
0.5-a
1-a
1-2a
关键:画出正态曲线的简图
解:
作出分布密度曲线如图示,由图可知,
σ=3
σ=2
x
y
O
1
-1
2
-2
例4.李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,出X和Y的分布密度曲线草图;
解:XN(30,62),YN(34,22)
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天有34min可用,李明应选择哪种交通工具?请说明理由.
(2)根据(1)中的估计结果,出X和Y的分布密度曲线草图
30
34
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天有34min可用,李明应选择哪种交通工具?请说明理由.
30
34
彩蛋:
1855年,清朝咸丰年间,高斯因心脏病发作去世。高斯被埋葬在哥根廷大学。但是下葬前,高斯的大佬被挖了出来,泡在瓶子里,放在哥根廷大学的实验室里供人研究。其中一位研究人员叫瓦格纳。瓦格纳一共研究了900多个大脑。有高级知识分子的,也有没受过教育的。瓦格纳研究大脑的很多参数,例如体积、重量、大脑皮层面积等。最后瓦格纳发现……
高斯的大脑的各种参数都在正态曲线的对称轴附近,和普通人的大脑的总体情况没有显著区别。
正态分布
这个计算非常困难,
有没有其他计算呢方法呢?
X 0 1 2 3 4 5 6
P
自动流水线包装的食盐,每袋标准质量为400 g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X的观测值(单位:g)如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
可用频率分布直方图描述这组误差数据的分布
正态分布又称为高斯分布
问题5:观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点?
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
0.5-a
1-a
1-2a
关键:画出正态曲线的简图
解:
作出分布密度曲线如图示,由图可知,
σ=3
σ=2
x
y
O
1
-1
2
-2
例4.李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,出X和Y的分布密度曲线草图;
解:XN(30,62),YN(34,22)
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天有34min可用,李明应选择哪种交通工具?请说明理由.
(2)根据(1)中的估计结果,出X和Y的分布密度曲线草图
30
34
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天有34min可用,李明应选择哪种交通工具?请说明理由.
30
34
彩蛋:
1855年,清朝咸丰年间,高斯因心脏病发作去世。高斯被埋葬在哥根廷大学。但是下葬前,高斯的大佬被挖了出来,泡在瓶子里,放在哥根廷大学的实验室里供人研究。其中一位研究人员叫瓦格纳。瓦格纳一共研究了900多个大脑。有高级知识分子的,也有没受过教育的。瓦格纳研究大脑的很多参数,例如体积、重量、大脑皮层面积等。最后瓦格纳发现……
高斯的大脑的各种参数都在正态曲线的对称轴附近,和普通人的大脑的总体情况没有显著区别。
