数学北师大版 七年级下册 5.3《简单的轴对称图形》第1课时 教案
文档属性
| 名称 | 数学北师大版 七年级下册 5.3《简单的轴对称图形》第1课时 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 00:00:00 | ||
图片预览



文档简介
第五章生活中的轴对称
5.3简单的轴对称图形
第1课时
一、教学目标
1.掌握等腰三角形的定义,利用定义解决问题;
2.掌握等腰三角形和等边三角形的轴对称性、相关性质及判定.
二、教学重点及难点
重点:等腰三角形的相关概念;掌握等腰三角形的轴对称性、有关性质及判定.
难点:应用等腰三角形的概念和性质解决等腰三角形解决问题.
三、教学准备
多媒体课件
四、相关资源
相关图片,微课,动画
五、教学过程
【问题情境】
在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,并且能够作出一个简单平面图形关于某一直线的轴对称图形,还能够通过轴对称变换来设计一些美丽的图案.这节课我们就从轴对称的角度来认识一些我们熟悉的几何图形.
问题1:三角形是轴对称图形吗?
有的三角形是轴对称图形,有的三角形不是.
问题2:什么样的三角形是轴对称图形?
满足轴对称的条件的三角形就是轴对称图形,也就是将三角形沿某一条直线对折后两部分能够完全重合的就是轴对称图形.
我们这节课就来认识一种是轴对称图形的三角形——等腰三角形.
设计意图:通过回顾轴对称图形及轴对称性质,引出本节课所要探究的内容,让学生明确探究方向.
【探究新知】
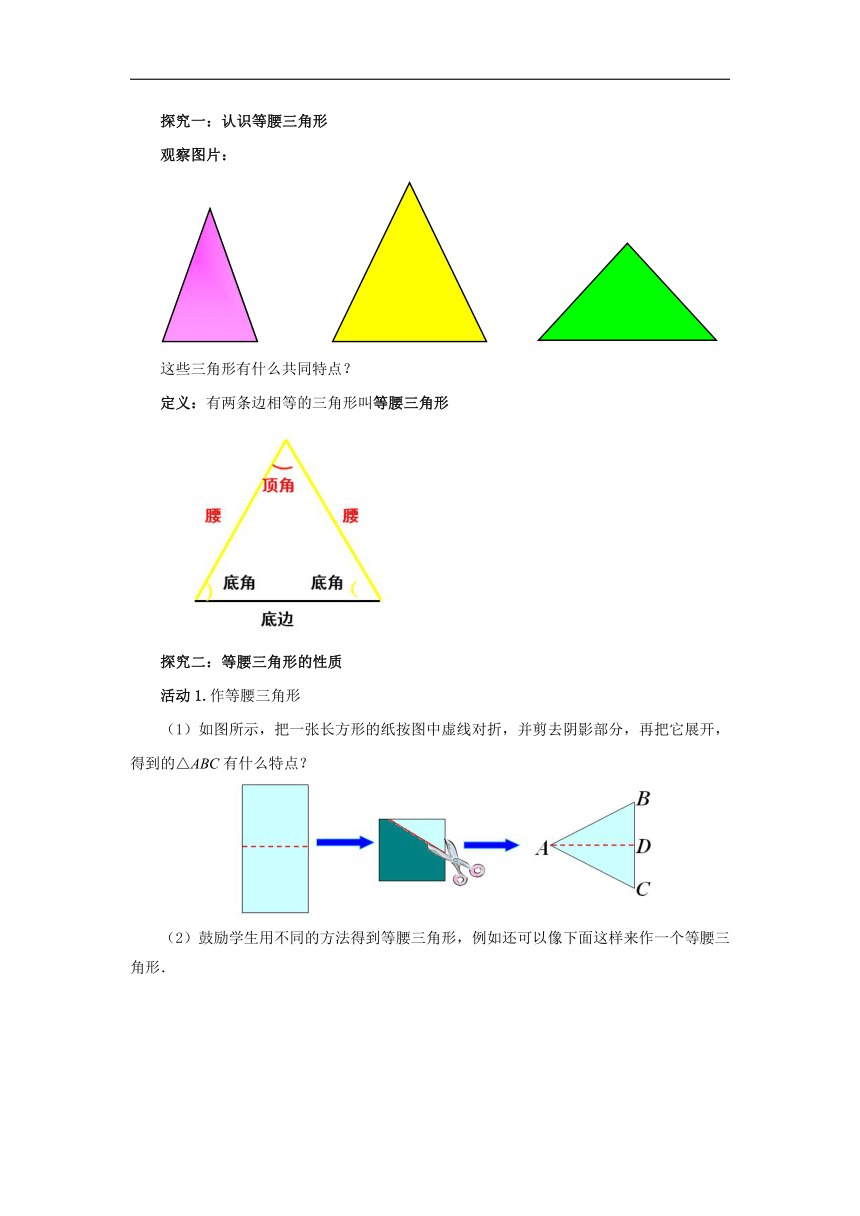
探究一:认识等腰三角形
观察图片:
这些三角形有什么共同特点?
定义:有两条边相等的三角形叫等腰三角形
探究二:等腰三角形的性质
活动1.作等腰三角形
(1)如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
(2)鼓励学生用不同的方法得到等腰三角形,例如还可以像下面这样来作一个等腰三角形.
作一条直线l,在l上取一点A,在l外取一点B,作出点B关于直线l的对称点C,连接AB,BC,CA,则可得到一个等腰三角形.
设计意图:以动手操作的形式得出一个等腰三角形,鼓励学生充分的进行交流,充分利用等腰三角形的特征,逆向思维,达到学以致用的目的.同时充分体现了数学来源于生活,同时也更好的服务于生活的理念.
活动2.思考:
(1)等腰三角形是轴对称图形吗?请找出它的对称轴.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗?
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗?底边上的高所在的直线呢?
(4)沿对称轴对折,你能发现等腰三角形的那些特征?说说你的理由.
因为等腰三角形的两腰相等,所以把这两条腰重合对折便知:等腰三角形是轴对称图形,它的对称轴是折痕所在的直线.
学生通过折叠,发现折痕两旁的部分互相重合,由此可知这个等腰三角形的两个底角相等,而且还可以知道顶角的平分线既是底边上的中线,也是底边上的高.
由此可以得到:
等腰三角形是轴对称图形.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”);
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
由上面折叠的过程获得启发,我们可以通过作出等腰三角形的对称轴,得到两个全等的三角形,从而利用三角形的全等来证明这些性质.
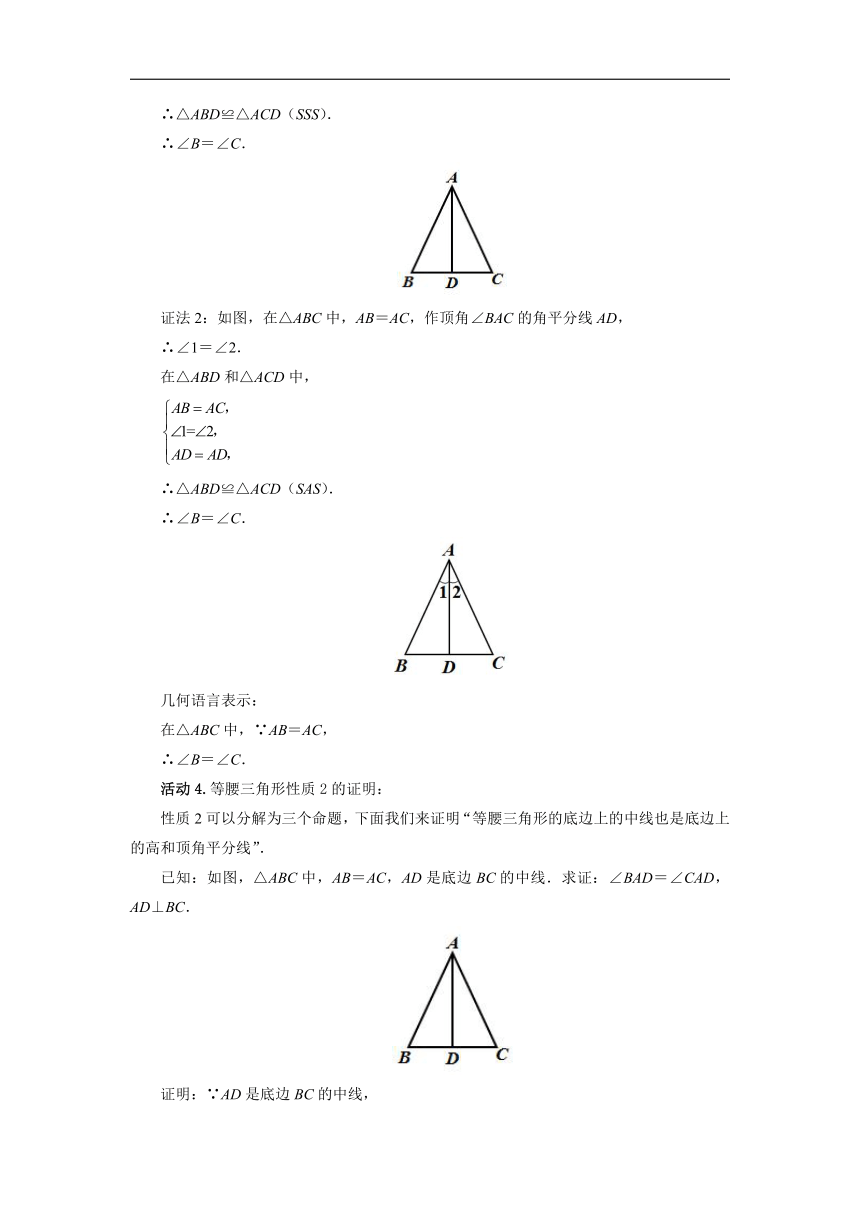
活动3.等腰三角形的性质1的证明:
证法1:如图,在△ABC中,AB=AC,作底边BC的中线AD,则BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠B=∠C.
证法2:如图,在△ABC中,AB=AC,作顶角∠BAC的角平分线AD,
∴∠1=∠2.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
几何语言表示:
在△ABC中,∵AB=AC,
∴∠B=∠C.
活动4.等腰三角形性质2的证明:
性质2可以分解为三个命题,下面我们来证明“等腰三角形的底边上的中线也是底边上的高和顶角平分线”.
已知:如图,△ABC中,AB=AC,AD是底边BC的中线.求证:∠BAD=∠CAD,AD⊥BC.
证明:∵AD是底边BC的中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,
∴∠ADB=90°.
∴AD⊥BC.
教师鼓励学生仿照示例口述另两个命题的证明过程.
几何语言表示:
在△ABC中,(1)∵AB=AC,BD=CD,
∴AD⊥BC,∠BAD=∠CAD.
(2)∵AB=AC,∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
(3)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在等腰三角形性质的探索过程和证明过程中,“折痕”“辅助线”发挥了非常重要的作用,由此得到:等腰三角形是轴对称图形,底边上的中线(或顶角平分线、底边上的高)所在直线就是它的对称轴.
设计意图:通过引导学生动手操作,探索和发现等腰三角形的性质,加深学生对等腰三角形性质的直观感知,并尝试构造全等三角形给出推理证明,锻炼学生探索和发现问题并解决问题的能力.
探究三:等边三角形
定义:三边都相等的三角形是等边三角形也叫正三角形.
2.性质:
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
结论:(1)等边三角形是轴对称图形;
(2)等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴;
(3)等边三角形的各角都相等,都等于60°.
设计意图:在等腰三角形的基础上学习等边三角形的定义及性质,等边三角形式等腰三角形的特例,具备等腰三角形的一切性质,又有独特性质,掌握等边三角形的特性是解决问题的关键.
【典型例题】
例1.已知:在△ABC中,AB=AC.
(1)若∠A=70°,则∠B=______,∠C=_______.
(2)若一个角为30°,则它的另外两内角分别为____________.
(3)若一角为100°,则它的另外两内角分别为____________.
分析:注意到题中所给的条件AB=AC,得到三角形为等腰三角形.利用等腰三角形的性质对问题(1)可得∠B=55°,∠C=55°;;对问题(2)考虑到所给这个角可能是顶角也可能是底角;对问题(3)由三角形内角和为180°可得此等腰三角形的顶角只能为100°这一种情况.
解:(1)∠B=55°,∠C=55°;
(2)另外两内角分别为:75°,75°或者30°,120°;
(3)40°,40°.
设计意图:通过题目中的(2)、(3)渗透分类思想,训练思维的严密性.
例2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求:△ABC各角的度数.
分析:根据“等边对等角”的性质,我们可以得到
∠A=∠ABD,∠ABC=∠C=∠BDC,
再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC的三个内角.
把∠A设为x的话,那么∠ABC,∠C都可以用x来表示,这样过程就更简捷.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°.
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
设计意图:通过逻辑推理和方程思想求出等腰三角形中的角的度数,让学生进一步巩固等腰三角形的性质“等角对等边”.
例3.如图,点D、E在△ABC的边BC上,AB=AC.
(1)若AD=AE,如图①,试说明:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,试说明:AF⊥BC.
解析:(1)过A作AG⊥BC于G.根据等腰三角形的性质得出BG=CG,DG=EG即可得出BD=CE;(2)先求出BF=CF,再根据等腰三角形的性质求解.
解:(1)如图①,过A作AG⊥BC于G.∵AB=AC,AD=AE,∴BG=CG,DG=EG,∴BG-DG=CG-EG,∴BD=CE;
(2)∵BD=CE,F为DE的中点,∴BD+DF=CE+EF,∴BF=CF.∵AB=AC,∴AF⊥BC.
设计意图:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
【随堂练习】
1.(1)如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( ).A
A.100° B.80° C.70° D.50°
(2)等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )A
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
(3)如果△ABC是轴对称图形,则它的对称轴一定是( ).C
A.某一条边上的高 B.某一条边上的中线
C.平分一角和这个角对边的直线 D.某一个角的平分线
设计意图:考查学生对轴对称图形及对称轴的理解和掌握.
(4)等腰三角形的一个外角是100°,它的顶角的度数是( ).C
A.80° B.20° C.80°或20° D.80°或50°
设计意图:考查学生运用等腰三角形性质1和三角形内角和等知识进行计算的能力.
(5)如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=2∠BAD;④.其中正确的有( ).D
A.1个 B.2个 C.3个 D.4个
设计意图:考查学生对等腰三角形性质的掌握.
2.(1)一等腰三角形的两边长为2和4,则该等腰三角形的周长为________.10
(2)一等腰三角形的两边长为3和4,则该等腰三角形的周长为_______.10或11
(3)已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长.
解:设三角形的底边长为xcm,则其腰长为(x+2)cm,根据题意得:
2(x+2)+x=16 解得 x=4
∴等腰三角形三边长为4cm,6cm,6cm.
设计意图:掌握等腰三角形中边长的计算,注意分类讨论三角形三边关系的综合运用.
3.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
说明:等边三角形是等腰三角形的特例,所以等腰三角形的性质对其都是适用的,在数学的学习时这样的情况是会经常出现的.
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
又∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
设计意图:综合运用等腰三角形性质、三角形内角和或者外角的性质等知识解决问题.使学生进一步巩固等腰三角形性质1,同时引导学生将与角有关的知识系统化,优化学生的知识结构.
4.已知:如图,P、Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
解:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
设计意图:考查等边三角形的性质、等腰三角形的性质以及三角形的外角的性质,能正确利用这些知识解决问题.
【课堂小结】
等腰三角形的性质
等边三角形的概念及性质
5.3简单的轴对称图形
第1课时
一、教学目标
1.掌握等腰三角形的定义,利用定义解决问题;
2.掌握等腰三角形和等边三角形的轴对称性、相关性质及判定.
二、教学重点及难点
重点:等腰三角形的相关概念;掌握等腰三角形的轴对称性、有关性质及判定.
难点:应用等腰三角形的概念和性质解决等腰三角形解决问题.
三、教学准备
多媒体课件
四、相关资源
相关图片,微课,动画
五、教学过程
【问题情境】
在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,并且能够作出一个简单平面图形关于某一直线的轴对称图形,还能够通过轴对称变换来设计一些美丽的图案.这节课我们就从轴对称的角度来认识一些我们熟悉的几何图形.
问题1:三角形是轴对称图形吗?
有的三角形是轴对称图形,有的三角形不是.
问题2:什么样的三角形是轴对称图形?
满足轴对称的条件的三角形就是轴对称图形,也就是将三角形沿某一条直线对折后两部分能够完全重合的就是轴对称图形.
我们这节课就来认识一种是轴对称图形的三角形——等腰三角形.
设计意图:通过回顾轴对称图形及轴对称性质,引出本节课所要探究的内容,让学生明确探究方向.
【探究新知】
探究一:认识等腰三角形
观察图片:
这些三角形有什么共同特点?
定义:有两条边相等的三角形叫等腰三角形
探究二:等腰三角形的性质
活动1.作等腰三角形
(1)如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
(2)鼓励学生用不同的方法得到等腰三角形,例如还可以像下面这样来作一个等腰三角形.
作一条直线l,在l上取一点A,在l外取一点B,作出点B关于直线l的对称点C,连接AB,BC,CA,则可得到一个等腰三角形.
设计意图:以动手操作的形式得出一个等腰三角形,鼓励学生充分的进行交流,充分利用等腰三角形的特征,逆向思维,达到学以致用的目的.同时充分体现了数学来源于生活,同时也更好的服务于生活的理念.
活动2.思考:
(1)等腰三角形是轴对称图形吗?请找出它的对称轴.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗?
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗?底边上的高所在的直线呢?
(4)沿对称轴对折,你能发现等腰三角形的那些特征?说说你的理由.
因为等腰三角形的两腰相等,所以把这两条腰重合对折便知:等腰三角形是轴对称图形,它的对称轴是折痕所在的直线.
学生通过折叠,发现折痕两旁的部分互相重合,由此可知这个等腰三角形的两个底角相等,而且还可以知道顶角的平分线既是底边上的中线,也是底边上的高.
由此可以得到:
等腰三角形是轴对称图形.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”);
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
由上面折叠的过程获得启发,我们可以通过作出等腰三角形的对称轴,得到两个全等的三角形,从而利用三角形的全等来证明这些性质.
活动3.等腰三角形的性质1的证明:
证法1:如图,在△ABC中,AB=AC,作底边BC的中线AD,则BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠B=∠C.
证法2:如图,在△ABC中,AB=AC,作顶角∠BAC的角平分线AD,
∴∠1=∠2.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
几何语言表示:
在△ABC中,∵AB=AC,
∴∠B=∠C.
活动4.等腰三角形性质2的证明:
性质2可以分解为三个命题,下面我们来证明“等腰三角形的底边上的中线也是底边上的高和顶角平分线”.
已知:如图,△ABC中,AB=AC,AD是底边BC的中线.求证:∠BAD=∠CAD,AD⊥BC.
证明:∵AD是底边BC的中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,
∴∠ADB=90°.
∴AD⊥BC.
教师鼓励学生仿照示例口述另两个命题的证明过程.
几何语言表示:
在△ABC中,(1)∵AB=AC,BD=CD,
∴AD⊥BC,∠BAD=∠CAD.
(2)∵AB=AC,∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
(3)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在等腰三角形性质的探索过程和证明过程中,“折痕”“辅助线”发挥了非常重要的作用,由此得到:等腰三角形是轴对称图形,底边上的中线(或顶角平分线、底边上的高)所在直线就是它的对称轴.
设计意图:通过引导学生动手操作,探索和发现等腰三角形的性质,加深学生对等腰三角形性质的直观感知,并尝试构造全等三角形给出推理证明,锻炼学生探索和发现问题并解决问题的能力.
探究三:等边三角形
定义:三边都相等的三角形是等边三角形也叫正三角形.
2.性质:
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
结论:(1)等边三角形是轴对称图形;
(2)等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴;
(3)等边三角形的各角都相等,都等于60°.
设计意图:在等腰三角形的基础上学习等边三角形的定义及性质,等边三角形式等腰三角形的特例,具备等腰三角形的一切性质,又有独特性质,掌握等边三角形的特性是解决问题的关键.
【典型例题】
例1.已知:在△ABC中,AB=AC.
(1)若∠A=70°,则∠B=______,∠C=_______.
(2)若一个角为30°,则它的另外两内角分别为____________.
(3)若一角为100°,则它的另外两内角分别为____________.
分析:注意到题中所给的条件AB=AC,得到三角形为等腰三角形.利用等腰三角形的性质对问题(1)可得∠B=55°,∠C=55°;;对问题(2)考虑到所给这个角可能是顶角也可能是底角;对问题(3)由三角形内角和为180°可得此等腰三角形的顶角只能为100°这一种情况.
解:(1)∠B=55°,∠C=55°;
(2)另外两内角分别为:75°,75°或者30°,120°;
(3)40°,40°.
设计意图:通过题目中的(2)、(3)渗透分类思想,训练思维的严密性.
例2.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求:△ABC各角的度数.
分析:根据“等边对等角”的性质,我们可以得到
∠A=∠ABD,∠ABC=∠C=∠BDC,
再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.
再由三角形内角和为180°,就可求出△ABC的三个内角.
把∠A设为x的话,那么∠ABC,∠C都可以用x来表示,这样过程就更简捷.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°.
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
设计意图:通过逻辑推理和方程思想求出等腰三角形中的角的度数,让学生进一步巩固等腰三角形的性质“等角对等边”.
例3.如图,点D、E在△ABC的边BC上,AB=AC.
(1)若AD=AE,如图①,试说明:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,试说明:AF⊥BC.
解析:(1)过A作AG⊥BC于G.根据等腰三角形的性质得出BG=CG,DG=EG即可得出BD=CE;(2)先求出BF=CF,再根据等腰三角形的性质求解.
解:(1)如图①,过A作AG⊥BC于G.∵AB=AC,AD=AE,∴BG=CG,DG=EG,∴BG-DG=CG-EG,∴BD=CE;
(2)∵BD=CE,F为DE的中点,∴BD+DF=CE+EF,∴BF=CF.∵AB=AC,∴AF⊥BC.
设计意图:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
【随堂练习】
1.(1)如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( ).A
A.100° B.80° C.70° D.50°
(2)等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )A
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
(3)如果△ABC是轴对称图形,则它的对称轴一定是( ).C
A.某一条边上的高 B.某一条边上的中线
C.平分一角和这个角对边的直线 D.某一个角的平分线
设计意图:考查学生对轴对称图形及对称轴的理解和掌握.
(4)等腰三角形的一个外角是100°,它的顶角的度数是( ).C
A.80° B.20° C.80°或20° D.80°或50°
设计意图:考查学生运用等腰三角形性质1和三角形内角和等知识进行计算的能力.
(5)如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=2∠BAD;④.其中正确的有( ).D
A.1个 B.2个 C.3个 D.4个
设计意图:考查学生对等腰三角形性质的掌握.
2.(1)一等腰三角形的两边长为2和4,则该等腰三角形的周长为________.10
(2)一等腰三角形的两边长为3和4,则该等腰三角形的周长为_______.10或11
(3)已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长.
解:设三角形的底边长为xcm,则其腰长为(x+2)cm,根据题意得:
2(x+2)+x=16 解得 x=4
∴等腰三角形三边长为4cm,6cm,6cm.
设计意图:掌握等腰三角形中边长的计算,注意分类讨论三角形三边关系的综合运用.
3.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
说明:等边三角形是等腰三角形的特例,所以等腰三角形的性质对其都是适用的,在数学的学习时这样的情况是会经常出现的.
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
又∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
设计意图:综合运用等腰三角形性质、三角形内角和或者外角的性质等知识解决问题.使学生进一步巩固等腰三角形性质1,同时引导学生将与角有关的知识系统化,优化学生的知识结构.
4.已知:如图,P、Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
解:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
设计意图:考查等边三角形的性质、等腰三角形的性质以及三角形的外角的性质,能正确利用这些知识解决问题.
【课堂小结】
等腰三角形的性质
等边三角形的概念及性质
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
