18.2.1 矩形 课时 1 同步练习(含解析)
文档属性
| 名称 | 18.2.1 矩形 课时 1 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 10:12:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章《平行四边形》练习
18.2.1矩形
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为-( )
A. 10cm B. 5cm C. 6cm D. 8cm
2.矩形具有而一般平行四边形不具有的性质是( )
A. 对角线相等 B. 对边相等 C. 对角相等 D. 对角线互相平分
3.矩形ABCD中, O是BC的中点,∠AOD=90°.矩形的周长为20cm ,则AB的长为( )
A. 1cm B. 2cm C. 2.5cm D. cm
4.已知如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC=( )cm.
A. 3 B. 4 C. 5 D. 6
5.如图所示,图(1)所示为长方形纸带,∠DEF=20o,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图3中的∠CFE的度数是( ).
A. 80 B. 100 C. 120 D. 140
二、填空题(每小题6分,共30分)
6.已知矩形的周长是40cm,被两条对角线分成的相邻两个三角形的周长的差是8cm,则较长的边长为____;
7.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为_____.
矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60 ,则这个矩形的对角线的长是________cm
9.如图,矩形ABCD中,E、F分别为AD、AB上一点,且EF=EC,EF⊥EC,若DE=2,矩形周长为16,则矩形ABCD的面积为_________
10.如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为_______.
三、解答题(共40分)
11.如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:
①△ABF≌△DCE
②AM=DM.
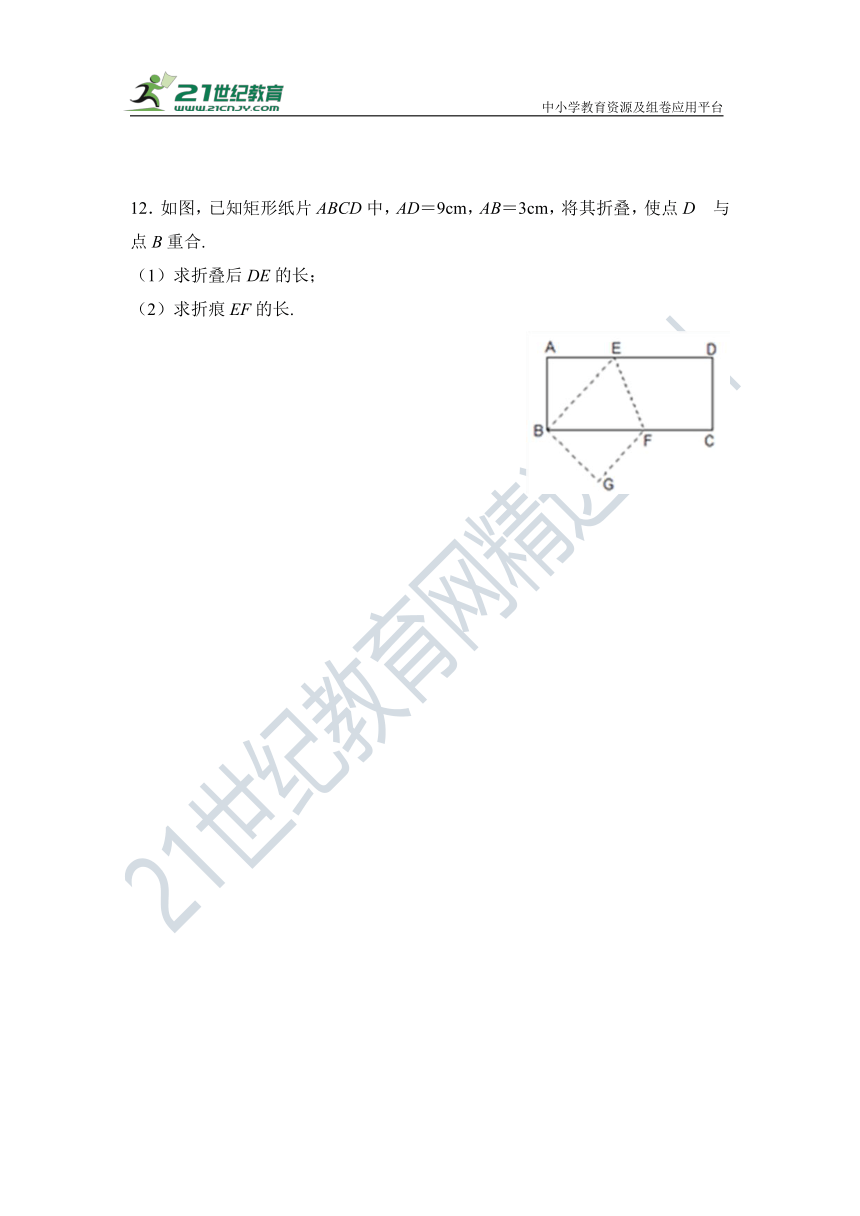
12.如图,已知矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点D 与点B重合.
(1)求折叠后DE的长;
(2)求折痕EF的长.
参考答案
1.B
【解析】如图,由题意可知,在矩形ABCD中,AC+BD=10cm,∠AOB=60°,
∴AC=BD=10cm,
∴AO=BO=5cm,
∴△AOB是等边三角形,
∴AB=AO=5cm.
故选B.
2.A
【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.
故选A.
3.D
【解析】解:∵O是BC中点,∴OB=OC.∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=90°.在△ABO和△DCO中,∵,∴△ABO≌△DCO(SAS),∴∠AOB=∠DOC.∵∠AOD=90°,∴∠AOB=∠DOC=45°,∴∠BAO=45°=∠AOB,∴AB=OB,BC=2AB.∵矩形ABCD的周长是20cm,∴2(AB+BC)=20cm,AB+BC=10cm,∴3AB=10cm,∴AB=cm.故选D.
4.A
【解析】解:由翻折的性质可得:AD=AF=BC=10cm.在Rt△ABF中可得:BF==6cm,∴FC=BC﹣BF=4cm,设CE=x,EF=DE=8﹣x,则在Rt△ECF中,EF2=EC2+CF2,即x2+16=(8﹣x)2,解得:x=3,故CE=3cm.故选A.
5.C
【解析】∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=20°.
由翻折的性质可知:图2中,∠EFC=180°-∠BFE=160°,∠BFC=∠EFC-∠BFE=140°,
∴图3中,∠CFE=∠BFC-∠BFE=120°.
故选:B.
6.14cm
【解析】设矩形的长边为a,短边为b,则2(a+b)=40①,a-b=8②,联立①②,解得a=14,故答案为14cm.
7.60°
【解析】延长AB交直线b于点E,
∵a∥b,
∴∠AEC=∠1=60°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠2=∠AEC=60°,
故答案为:60°.
8.8
【解析】因为四边形ABCD是矩形,所以OA=OB=OC=OD,AC=2OA,因为∠AOB=60°,所以△AOB是等边三角形,所以OA=OB=AB=4,所以AC=2×4=8,故答案为8.
9.15
【解析】因为EF⊥EC,所以∠FEC=90°,所以∠AEF+∠DEC=90°,因为∠AEF+∠AFE=90°,所以∠AFE=∠DEC,因为∠A=∠D,EF=CE,所以△AEF≌△DCE,所以AE=CD,AF=DE,设AB=CD=x,则AD=AE+DE=CD+DE=x+2,所以2(x+x+2)=16,解得x=3,所以AB×BC=3×(3+2)=15,故答案为15.
10.20
【解析】∵四边形ABCD为矩形,∴∠A=∠D=90°,在Rt△ABM中,AB=8,AM=6,由勾股定理得BM=10,同理CM=10,∵E、F分别是线段BM、CM的中点,BN=CN,∴EM=FM=5,∴EN,FN都是△BCM的中位线,∴EN=FN=5,∴四边形ENFM的周长为5+5+5+5=20,故答案为20.
11.见解析
【解析】①用SAS证明△ABF≌△DCE;(2)由△ABF≌△DCE得∠AFB=∠DEC,再结合AD∥BC,得∠MAD=∠MDA,用等角对等边证明MA=MD.
证明:①∵四边形ABCD为矩形,
∴AB=DC,∠B=∠C,
∵BE=CF,
∴BE+EF=EF+CF,即BF=CE,
在△ABF和△DCE中
∴△ABF≌△DCE(SAS);
②∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∵AD∥BC,
∴∠AFB=∠MAD,∠DEC=∠MDA,
∴∠MAD=∠MDA,
∴MA=MD.
12.(1)5;(2)
【解析】(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,根据勾股定理得出AE2+AB2=BE2,即(9-x)2+32=x2,解方程求出x,即可得出DE的长;
(2)连接BD,作EG⊥BC于G,则四边形ABGE是矩形,∠EGF=90°,得出EG=AB=3,BG=AE=4,得出GF=1,由勾股定理求出EF2,即可得出EF的长.
解:(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,
∵四边形ABCD是矩形,
∴∠A=90°,
根据勾股定理得:AE2+AB2=BE2,
即(9-x)2+32=x2,
解得:x=5,
即DE长为5cm,
(2)作EG⊥BC于G,如图所示:
则四边形ABGE是矩形,∠EGF=90°,
∴EG=AB=3,BG=AE=4,
∴GF=1,
∴EF2=EG2+GF2=32+12=10,
∴EF=
第18章《平行四边形》练习
18.2.1矩形
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为-( )
A. 10cm B. 5cm C. 6cm D. 8cm
2.矩形具有而一般平行四边形不具有的性质是( )
A. 对角线相等 B. 对边相等 C. 对角相等 D. 对角线互相平分
3.矩形ABCD中, O是BC的中点,∠AOD=90°.矩形的周长为20cm ,则AB的长为( )
A. 1cm B. 2cm C. 2.5cm D. cm
4.已知如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm,则EC=( )cm.
A. 3 B. 4 C. 5 D. 6
5.如图所示,图(1)所示为长方形纸带,∠DEF=20o,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图3中的∠CFE的度数是( ).
A. 80 B. 100 C. 120 D. 140
二、填空题(每小题6分,共30分)
6.已知矩形的周长是40cm,被两条对角线分成的相邻两个三角形的周长的差是8cm,则较长的边长为____;
7.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为_____.
矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60 ,则这个矩形的对角线的长是________cm
9.如图,矩形ABCD中,E、F分别为AD、AB上一点,且EF=EC,EF⊥EC,若DE=2,矩形周长为16,则矩形ABCD的面积为_________
10.如图,在矩形ABCD中,M.N.分别是边AD,BC 的中点,点E、点F分别是线段BM,CN的中点,若AM=DM=6,AB=8,则四边形ENFM的周长为_______.
三、解答题(共40分)
11.如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:
①△ABF≌△DCE
②AM=DM.
12.如图,已知矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点D 与点B重合.
(1)求折叠后DE的长;
(2)求折痕EF的长.
参考答案
1.B
【解析】如图,由题意可知,在矩形ABCD中,AC+BD=10cm,∠AOB=60°,
∴AC=BD=10cm,
∴AO=BO=5cm,
∴△AOB是等边三角形,
∴AB=AO=5cm.
故选B.
2.A
【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.
故选A.
3.D
【解析】解:∵O是BC中点,∴OB=OC.∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=90°.在△ABO和△DCO中,∵,∴△ABO≌△DCO(SAS),∴∠AOB=∠DOC.∵∠AOD=90°,∴∠AOB=∠DOC=45°,∴∠BAO=45°=∠AOB,∴AB=OB,BC=2AB.∵矩形ABCD的周长是20cm,∴2(AB+BC)=20cm,AB+BC=10cm,∴3AB=10cm,∴AB=cm.故选D.
4.A
【解析】解:由翻折的性质可得:AD=AF=BC=10cm.在Rt△ABF中可得:BF==6cm,∴FC=BC﹣BF=4cm,设CE=x,EF=DE=8﹣x,则在Rt△ECF中,EF2=EC2+CF2,即x2+16=(8﹣x)2,解得:x=3,故CE=3cm.故选A.
5.C
【解析】∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=20°.
由翻折的性质可知:图2中,∠EFC=180°-∠BFE=160°,∠BFC=∠EFC-∠BFE=140°,
∴图3中,∠CFE=∠BFC-∠BFE=120°.
故选:B.
6.14cm
【解析】设矩形的长边为a,短边为b,则2(a+b)=40①,a-b=8②,联立①②,解得a=14,故答案为14cm.
7.60°
【解析】延长AB交直线b于点E,
∵a∥b,
∴∠AEC=∠1=60°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠2=∠AEC=60°,
故答案为:60°.
8.8
【解析】因为四边形ABCD是矩形,所以OA=OB=OC=OD,AC=2OA,因为∠AOB=60°,所以△AOB是等边三角形,所以OA=OB=AB=4,所以AC=2×4=8,故答案为8.
9.15
【解析】因为EF⊥EC,所以∠FEC=90°,所以∠AEF+∠DEC=90°,因为∠AEF+∠AFE=90°,所以∠AFE=∠DEC,因为∠A=∠D,EF=CE,所以△AEF≌△DCE,所以AE=CD,AF=DE,设AB=CD=x,则AD=AE+DE=CD+DE=x+2,所以2(x+x+2)=16,解得x=3,所以AB×BC=3×(3+2)=15,故答案为15.
10.20
【解析】∵四边形ABCD为矩形,∴∠A=∠D=90°,在Rt△ABM中,AB=8,AM=6,由勾股定理得BM=10,同理CM=10,∵E、F分别是线段BM、CM的中点,BN=CN,∴EM=FM=5,∴EN,FN都是△BCM的中位线,∴EN=FN=5,∴四边形ENFM的周长为5+5+5+5=20,故答案为20.
11.见解析
【解析】①用SAS证明△ABF≌△DCE;(2)由△ABF≌△DCE得∠AFB=∠DEC,再结合AD∥BC,得∠MAD=∠MDA,用等角对等边证明MA=MD.
证明:①∵四边形ABCD为矩形,
∴AB=DC,∠B=∠C,
∵BE=CF,
∴BE+EF=EF+CF,即BF=CE,
在△ABF和△DCE中
∴△ABF≌△DCE(SAS);
②∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∵AD∥BC,
∴∠AFB=∠MAD,∠DEC=∠MDA,
∴∠MAD=∠MDA,
∴MA=MD.
12.(1)5;(2)
【解析】(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,根据勾股定理得出AE2+AB2=BE2,即(9-x)2+32=x2,解方程求出x,即可得出DE的长;
(2)连接BD,作EG⊥BC于G,则四边形ABGE是矩形,∠EGF=90°,得出EG=AB=3,BG=AE=4,得出GF=1,由勾股定理求出EF2,即可得出EF的长.
解:(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,
∵四边形ABCD是矩形,
∴∠A=90°,
根据勾股定理得:AE2+AB2=BE2,
即(9-x)2+32=x2,
解得:x=5,
即DE长为5cm,
(2)作EG⊥BC于G,如图所示:
则四边形ABGE是矩形,∠EGF=90°,
∴EG=AB=3,BG=AE=4,
∴GF=1,
∴EF2=EG2+GF2=32+12=10,
∴EF=
