18.2.2 菱形 课时 1 同步练习(含解析)
文档属性
| 名称 | 18.2.2 菱形 课时 1 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 567.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第18章《平行四边形》练习
18.2.2菱形
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.已知:如图,在矩形ABCD中,E ,F ,G ,H分别为边AB, BC ,CD, DA的中点.若AB=2,AD=4,则图中阴影部分的面积为 ( )
A. 5 B. 4.5 C. 4 D. 3.5
2.如图,菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
A. AB∥DC B. AC=BD C. AC⊥BD D. OA=OC
3.如图四边形ABCD是菱形,对角线AC=8,BD=6,DH⊥AB于点H,则DH的长度是( )
A. B. C. D.
4.如图,已知菱形ABCD的周长为16,面积为,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A. 2 B. 2 C. 4 D. 4
5.如果a表示一个菱形的对角线的平方和,b表示这个菱形的一边的平方,那么( )
A. a=4b B. a=2b C. a=b D. b=4a
二、填空题(每小题6分,共30分)
6.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是________cm2.
7.如图,菱形花坛的边长为6cm,一个内角为60°,在花坛中用花盆围出两个正六边形的图形(图中粗线部分),则围出的图形的周长为___________ cm.
8.如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=_____.
9.已知菱形ABCD的两条对角线相交于点O,AC=4,BD=2,则菱形ABCD的周长是___________.
10.如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为_________.
三、解答题(共40分)
11.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
求证:(1)四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
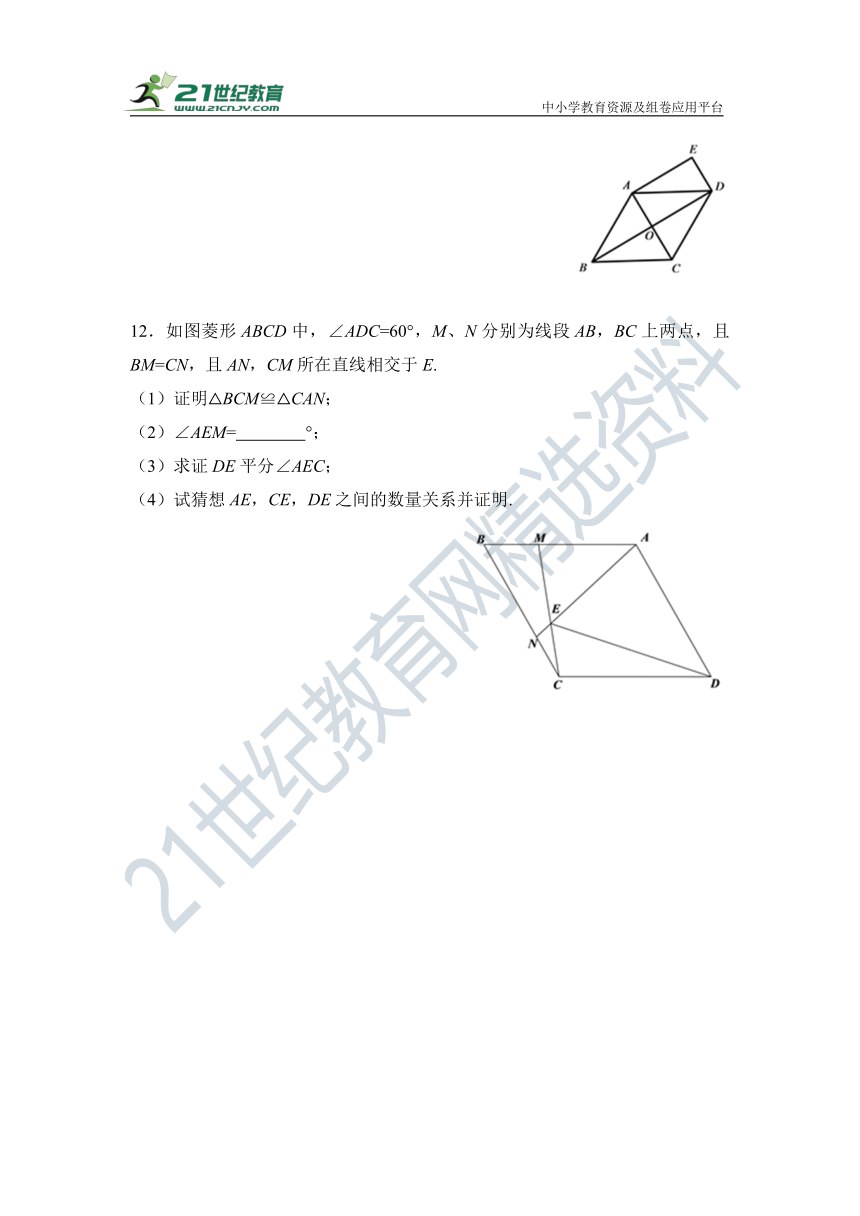
12.如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
参考答案
1.C
【解析】连接AC,BD,FH,EG,
∵四边形ABCD是矩形,
∴AC=BD,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴HG=AC,EF∥AC,EF=AC,EH=BD,GF=BD,
∴EH=HG =EF=GF,
∴平行四边形EFGH是菱形,
∴FH⊥EG,
∴阴影部分EFGH的面积是×HF×EG=×2×4=4,
故选C.
2.B
【解析】∵四边形ABCD是菱形,
∴AB∥DC,故选项A正确,不合题意;
无法得出AC=BD,故选项B错误,符合题意;
AC⊥BD,故选项C正确,不合题意;
OA=OC,故选项D正确,不合题意;
故选B.
3.C
【解析】∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥BD,OA=OC=4,OB=OD=3,
∴AB=5cm,
∴S菱形ABCD=AC·BD=AB·DH,
∴DH=.
故选C.
4.B
【解析】如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′=,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P‘E的值最小,最小值为CE的长=2,
故选:B.
5.A
【解析】设菱形的两条对角线分别为2m,2n,则a=(2m)2+(2n)2=4(m2+n2),则勾股定理得b=m2+n2,所以a=4b,故选A.
6.30
【解析】菱形的面积=×5×12=30(cm2).
故答案为:30.
7.20
【解析】如图,每个三角形都为等边三角形,由于图形中是两个正六边形,菱形花坛的边长为6cm,则每个正三角形的边长为2cm,则围出的图形的周长为 cm.
故答案:20.
8.30°
【解析】由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为:30°.
9.
【解析】根据菱形的对角线相互平分,则OA=2,OB=1,根据对角线垂直,则AB= ,则菱形ABCD的周长是.
故答案:.
10.
【解析】菱形的一条对角线为矩形的对角线时,面积最大,作出图形,设边长为x,表示出BE=10-x,再利用勾股定理列式计算求出x,然后根据菱形的四条边都相等列式进行计算即可得解出边长,再计算面积即可.
解:如图,菱形的一条对角线与矩形的对角线重合时,面积最大,
设AB=BC=x,则BE=10-x,
在Rt△BCE中,BC2=BE2+CE2,
即x2=(10-x)2+22,
解得x=,
所以S菱形ABCD=×2=.
故答案为:.
11.(1)见解析(2)9
【解析】(1)由已知易得四边形AODE是平行四边形,由四边形ABCD是菱形可得AC⊥BD,从而可得∠AOD=90°,由此可得平行四边形AODE是矩形;
(2)由四边形ABCD是菱形,∠BCD=120°易证△ABC是等边三角形,从而可得AC=AB=6,AO=3,结合AC⊥BD由勾股定理可得BO=3,则OD=3,由此可得矩形AODE的面积为.
解:(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=×4=2,
∵在菱形ABCD中,AC⊥BD,
∴由勾股定理OB=3,
∵四边形ABCD是菱形,
∴OD=OB=3,
∴四边形AODE的面积=OA OD=9.
12.(1)证明见解析;(2)60°;(3)证明见解析;(4)ED=EC+AE,理由见解析.
【解析】(1)如图,连接AC.由题意△ABC,△ADC都是等边三角形,根据SAS即可证明△BCM≌△CAN.
(2)由△BCM≌△CAN,推出∠BCM=∠CAN,推出∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
(3)如图中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.由△DGA≌△DHC,推出DG=DH,由DG⊥AN,DH⊥MC,推出∠DEG=∠DEH.即DE平分∠AEC.
(4)结论:EA+EC=ED.由(3)可知,∠GED=60°,在Rt△DEG中,由∠EDG=30°,推出DE=2EG,易证△DEG≌△DEH,推出EG=EH,推出EA+EC=EG+AG+EH-CH,由△DGA≌△DHC,推出GA=CH,推出EA+EC=2EG=DE,
解:(1)如图1中,连接AC.
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠ADC=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
,
∴△BCM≌△CAN.
(2)如图1中,∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
故答案为60.
(3)如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.
∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
,
∴△DGA≌△DHC,
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH.
∴DE平分∠AEC.
(4)结论:EA+EC=ED.理由如下:
如图2中,由(3)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
易知△DEG≌△DEH,
∴EG=EH,
∴EA+EC=EG+AG+EH-CH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=2EG=DE,
∴EA+EC=ED.
第18章《平行四边形》练习
18.2.2菱形
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.已知:如图,在矩形ABCD中,E ,F ,G ,H分别为边AB, BC ,CD, DA的中点.若AB=2,AD=4,则图中阴影部分的面积为 ( )
A. 5 B. 4.5 C. 4 D. 3.5
2.如图,菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
A. AB∥DC B. AC=BD C. AC⊥BD D. OA=OC
3.如图四边形ABCD是菱形,对角线AC=8,BD=6,DH⊥AB于点H,则DH的长度是( )
A. B. C. D.
4.如图,已知菱形ABCD的周长为16,面积为,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A. 2 B. 2 C. 4 D. 4
5.如果a表示一个菱形的对角线的平方和,b表示这个菱形的一边的平方,那么( )
A. a=4b B. a=2b C. a=b D. b=4a
二、填空题(每小题6分,共30分)
6.已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是________cm2.
7.如图,菱形花坛的边长为6cm,一个内角为60°,在花坛中用花盆围出两个正六边形的图形(图中粗线部分),则围出的图形的周长为___________ cm.
8.如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=_____.
9.已知菱形ABCD的两条对角线相交于点O,AC=4,BD=2,则菱形ABCD的周长是___________.
10.如图,由两个长为10,宽为2的矩形叠合而得到菱形ABCD,则菱形ABCD面积的最大值为_________.
三、解答题(共40分)
11.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
求证:(1)四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
12.如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
参考答案
1.C
【解析】连接AC,BD,FH,EG,
∵四边形ABCD是矩形,
∴AC=BD,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴HG=AC,EF∥AC,EF=AC,EH=BD,GF=BD,
∴EH=HG =EF=GF,
∴平行四边形EFGH是菱形,
∴FH⊥EG,
∴阴影部分EFGH的面积是×HF×EG=×2×4=4,
故选C.
2.B
【解析】∵四边形ABCD是菱形,
∴AB∥DC,故选项A正确,不合题意;
无法得出AC=BD,故选项B错误,符合题意;
AC⊥BD,故选项C正确,不合题意;
OA=OC,故选项D正确,不合题意;
故选B.
3.C
【解析】∵四边形ABCD是菱形,AC=8,BD=6,
∴AC⊥BD,OA=OC=4,OB=OD=3,
∴AB=5cm,
∴S菱形ABCD=AC·BD=AB·DH,
∴DH=.
故选C.
4.B
【解析】如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′=,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P‘E的值最小,最小值为CE的长=2,
故选:B.
5.A
【解析】设菱形的两条对角线分别为2m,2n,则a=(2m)2+(2n)2=4(m2+n2),则勾股定理得b=m2+n2,所以a=4b,故选A.
6.30
【解析】菱形的面积=×5×12=30(cm2).
故答案为:30.
7.20
【解析】如图,每个三角形都为等边三角形,由于图形中是两个正六边形,菱形花坛的边长为6cm,则每个正三角形的边长为2cm,则围出的图形的周长为 cm.
故答案:20.
8.30°
【解析】由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为:30°.
9.
【解析】根据菱形的对角线相互平分,则OA=2,OB=1,根据对角线垂直,则AB= ,则菱形ABCD的周长是.
故答案:.
10.
【解析】菱形的一条对角线为矩形的对角线时,面积最大,作出图形,设边长为x,表示出BE=10-x,再利用勾股定理列式计算求出x,然后根据菱形的四条边都相等列式进行计算即可得解出边长,再计算面积即可.
解:如图,菱形的一条对角线与矩形的对角线重合时,面积最大,
设AB=BC=x,则BE=10-x,
在Rt△BCE中,BC2=BE2+CE2,
即x2=(10-x)2+22,
解得x=,
所以S菱形ABCD=×2=.
故答案为:.
11.(1)见解析(2)9
【解析】(1)由已知易得四边形AODE是平行四边形,由四边形ABCD是菱形可得AC⊥BD,从而可得∠AOD=90°,由此可得平行四边形AODE是矩形;
(2)由四边形ABCD是菱形,∠BCD=120°易证△ABC是等边三角形,从而可得AC=AB=6,AO=3,结合AC⊥BD由勾股定理可得BO=3,则OD=3,由此可得矩形AODE的面积为.
解:(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=×4=2,
∵在菱形ABCD中,AC⊥BD,
∴由勾股定理OB=3,
∵四边形ABCD是菱形,
∴OD=OB=3,
∴四边形AODE的面积=OA OD=9.
12.(1)证明见解析;(2)60°;(3)证明见解析;(4)ED=EC+AE,理由见解析.
【解析】(1)如图,连接AC.由题意△ABC,△ADC都是等边三角形,根据SAS即可证明△BCM≌△CAN.
(2)由△BCM≌△CAN,推出∠BCM=∠CAN,推出∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
(3)如图中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.由△DGA≌△DHC,推出DG=DH,由DG⊥AN,DH⊥MC,推出∠DEG=∠DEH.即DE平分∠AEC.
(4)结论:EA+EC=ED.由(3)可知,∠GED=60°,在Rt△DEG中,由∠EDG=30°,推出DE=2EG,易证△DEG≌△DEH,推出EG=EH,推出EA+EC=EG+AG+EH-CH,由△DGA≌△DHC,推出GA=CH,推出EA+EC=2EG=DE,
解:(1)如图1中,连接AC.
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠ADC=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
,
∴△BCM≌△CAN.
(2)如图1中,∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
故答案为60.
(3)如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.
∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
,
∴△DGA≌△DHC,
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH.
∴DE平分∠AEC.
(4)结论:EA+EC=ED.理由如下:
如图2中,由(3)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
易知△DEG≌△DEH,
∴EG=EH,
∴EA+EC=EG+AG+EH-CH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=2EG=DE,
∴EA+EC=ED.
