18.1.1 平行四边形的性质 课时 1 同步练习(含解析)
文档属性
| 名称 | 18.1.1 平行四边形的性质 课时 1 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章《平行四边形》练习
18.1.1 平行四边形的性质
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是( ).
A. B. C. D.
2.如图,四边形ABCD为平行四边形,蚂蚁甲沿A-B-C从A到C,蚂蚁乙沿B-C-D从B到D,两只蚂蚁速度相同且同时出发,则下列结论中,错误的是( )
A. 甲到达B点时,乙也正好到达C点 B. 甲、乙同时到达终点
C. 甲、乙所经过的路程相同 D. 甲、乙所用的时间相同
第2题图 第3题图
3.如图,平行四边形中,,,于,则等于( ).
A. B. C. D.
4.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的,那么BC的长是( )
A. 6 B. 8 C. 10 D. 16
5.在□ABCD中,,平分交于点,平分交于点,且,则的长为( )
A. B. C. 或 D. 或
二、填空题(每小题6分,共30分)
6.在□ABCD中,∠B +∠D=200°,则∠A=__________°.
7.平行四边形两邻边长分别为20和16,若两条较长边之间的距离为6,则两条较短边之间的距离为_______.
8.在□ABCD中,若∠A∶∠B=1∶2,那么∠D-∠C=__________.
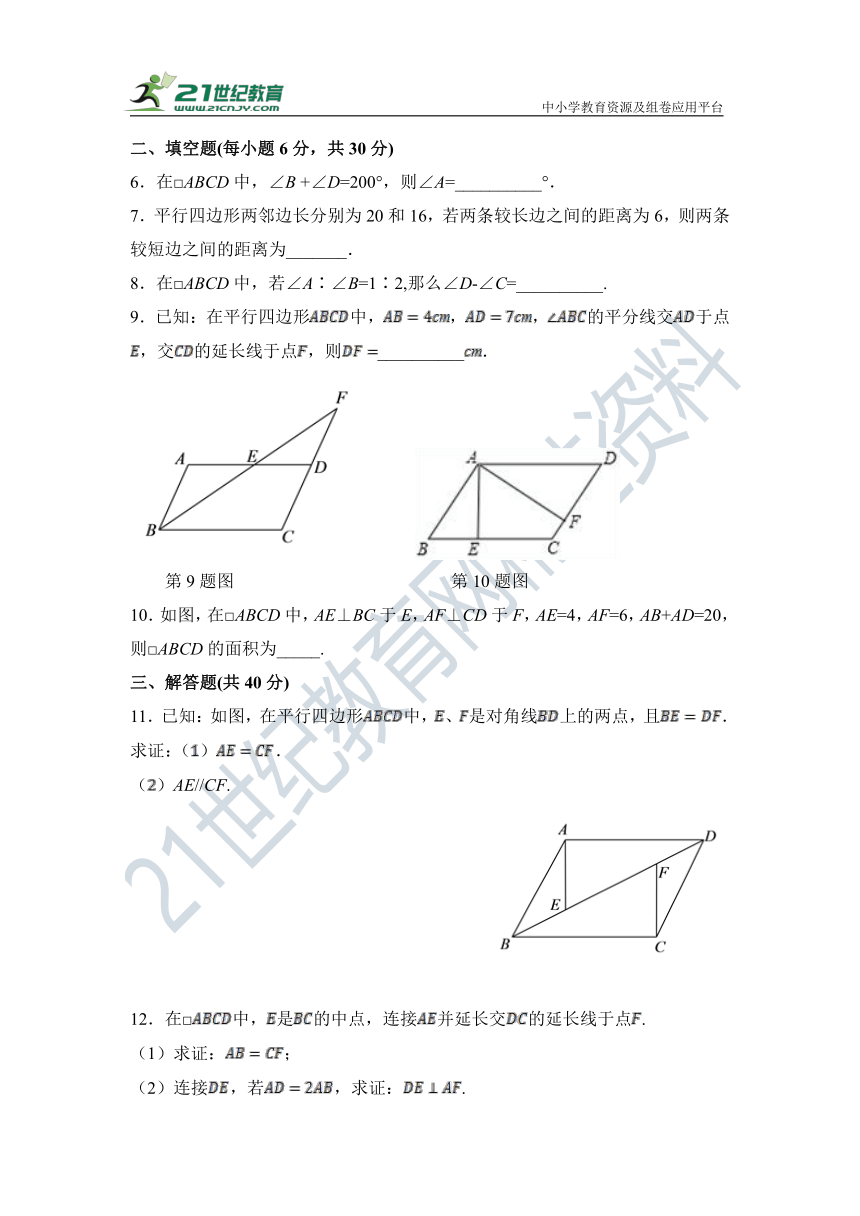
9.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.
第9题图 第10题图
10.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,AB+AD=20,则□ABCD的面积为_____.
三、解答题(共40分)
11.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
()AE//CF.
12.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
参考答案
1.B
【解析】∵平行四边形,有两个内角的比为,且这两个内角和为,
∴较小的内角度数为: ,
故选.
2.A
【解析】∵四边形ABCD为平行四边形,
∴AB=CD,
∴AB+BC=BC+CD,
即可知甲、乙所经过的路程相同;
又∵两只蚂蚁速度相同且同时出发,
∴甲、乙所用的时间相同且甲、乙同时到达终点.
故B、C、D正确.
故选A.
3.A
【解析】∵,
∴,
∴,
∵平行四边形,
∴DC//AB,
∴,
∵,
∴,
∴.
故选A.
4.C
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:6÷=32,
∴AB+BC=×32=16,
∴BC=10.
故选C.
5.D
【解析】①
∵平行四边形ABCD,∴AD=BC=8,AB=CD,AD∥BC,∴∠DAE=∠AEB,
∵EA平分∠BAD,∴∠BAE=∠EAD,∴∠BAE=∠AEB,∴AB=BE,
同理可证:CD=CF,∴AB=BE=CD=CF,
∴BC=BE+CF-EF=2AB-2=8,即AB=5;
②
∵平行四边形ABCD,∴AD=BC=8,AB=CD,AD∥BC,∴∠DAE=∠AEB,
∵EA平分∠BAD,∴∠BAE=∠EAD,∴∠BAE=∠AEB,∴AB=BE,
同理可证:CD=CF,∴AB=BE=CD=CF,
∴BC=BE+CF+EF=2AB+2=8,即AB=3;
∴AB=3或5.
故选D.
6.80
【解析】∵平行四边形ABCD,∴∠B=∠D,
∵∠B +∠D=200°,∴∠B=∠D=100°,
∴∠A=180°-100°=80°.
故答案为80.
7.7.5
【解析】由题意得
20×6÷16=7.5cm.
8.60°
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
又∵∠A:∠B=1:2,
∴∠A=60°,∠B=120°,
∴∠C=60°,∠D=120°,
∴∠D-∠C=120°-60°=60°.
故答案为:60°.
9.3
【解析】∵四边形ABCD是平行四边形,
∴BC=AD=7cm,CD=AB=4cm,CD∥AB,
∴∠F=∠ABF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠F=∠CBF,
∴CF=BC=7cm,
∴DF=CF-CD=7-4=3(cm).
故答案为:3.
10.48
【解析】设BC=x,∵AB+AD=20, 所以BC+CD=20,∴CD=20-x,
∵□ABCD的面积=BC AE=CD AF,∴4x=6(20-x),解得x=12,
∴□ABCD的面积=BC AE=12×4=48,
故答案为:48.
11.(1)证明见解析(2)证明见解析
【解析】(1)根据平行四边形性质得到AB=CD,AB∥CD,再得到∠ABE=∠CDF,根据“有两边和它们的夹角对应相等的两个三角形全等”得到△ABE≌△CDF,据此可得到即可AE=CF;(2)由△ABE≌△CDF可得∠AEB=∠CFD,再根据“等角的补角相等”得到∠AED=∠CFB,再根据“内错角相等,两直线平行”得到AE∥CF即可.
证明:()∵平行四边形
∴,
.
∴.
在和中,
∴≌,
∴
()∵≌,
∴
∴
∴.
12.证明见解析
【解析】(1)要证明AB=CF可通过△AEB≌△FEC证得,利用平行四边形ABCD的性质不难证明;(2)由平行四边形ABCD的性质可得AB=CD,由△AEB≌△FEC可得AB=CF,所以DF=2CF=2AB,所以AD=DF,由等腰三角形三线合一的性质可证得ED⊥AF .
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠F,
∵E是BC的中点,
∴BE=CE,
在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS),
∴AB=CF;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=CF,DF=DC+CF ,
∴DF=2CF,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵△AEB≌△FEC,
∴AE=EF,
∴ED⊥AF .
第18章《平行四边形》练习
18.1.1 平行四边形的性质
第1课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.平行四边形中,有两个内角的比为,则这个平行四边形中较小的内角是( ).
A. B. C. D.
2.如图,四边形ABCD为平行四边形,蚂蚁甲沿A-B-C从A到C,蚂蚁乙沿B-C-D从B到D,两只蚂蚁速度相同且同时出发,则下列结论中,错误的是( )
A. 甲到达B点时,乙也正好到达C点 B. 甲、乙同时到达终点
C. 甲、乙所经过的路程相同 D. 甲、乙所用的时间相同
第2题图 第3题图
3.如图,平行四边形中,,,于,则等于( ).
A. B. C. D.
4.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的,那么BC的长是( )
A. 6 B. 8 C. 10 D. 16
5.在□ABCD中,,平分交于点,平分交于点,且,则的长为( )
A. B. C. 或 D. 或
二、填空题(每小题6分,共30分)
6.在□ABCD中,∠B +∠D=200°,则∠A=__________°.
7.平行四边形两邻边长分别为20和16,若两条较长边之间的距离为6,则两条较短边之间的距离为_______.
8.在□ABCD中,若∠A∶∠B=1∶2,那么∠D-∠C=__________.
9.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.
第9题图 第10题图
10.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,AB+AD=20,则□ABCD的面积为_____.
三、解答题(共40分)
11.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
()AE//CF.
12.在□中,是的中点,连接并延长交的延长线于点.
(1)求证:;
(2)连接,若,求证:.
参考答案
1.B
【解析】∵平行四边形,有两个内角的比为,且这两个内角和为,
∴较小的内角度数为: ,
故选.
2.A
【解析】∵四边形ABCD为平行四边形,
∴AB=CD,
∴AB+BC=BC+CD,
即可知甲、乙所经过的路程相同;
又∵两只蚂蚁速度相同且同时出发,
∴甲、乙所用的时间相同且甲、乙同时到达终点.
故B、C、D正确.
故选A.
3.A
【解析】∵,
∴,
∴,
∵平行四边形,
∴DC//AB,
∴,
∵,
∴,
∴.
故选A.
4.C
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:6÷=32,
∴AB+BC=×32=16,
∴BC=10.
故选C.
5.D
【解析】①
∵平行四边形ABCD,∴AD=BC=8,AB=CD,AD∥BC,∴∠DAE=∠AEB,
∵EA平分∠BAD,∴∠BAE=∠EAD,∴∠BAE=∠AEB,∴AB=BE,
同理可证:CD=CF,∴AB=BE=CD=CF,
∴BC=BE+CF-EF=2AB-2=8,即AB=5;
②
∵平行四边形ABCD,∴AD=BC=8,AB=CD,AD∥BC,∴∠DAE=∠AEB,
∵EA平分∠BAD,∴∠BAE=∠EAD,∴∠BAE=∠AEB,∴AB=BE,
同理可证:CD=CF,∴AB=BE=CD=CF,
∴BC=BE+CF+EF=2AB+2=8,即AB=3;
∴AB=3或5.
故选D.
6.80
【解析】∵平行四边形ABCD,∴∠B=∠D,
∵∠B +∠D=200°,∴∠B=∠D=100°,
∴∠A=180°-100°=80°.
故答案为80.
7.7.5
【解析】由题意得
20×6÷16=7.5cm.
8.60°
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
又∵∠A:∠B=1:2,
∴∠A=60°,∠B=120°,
∴∠C=60°,∠D=120°,
∴∠D-∠C=120°-60°=60°.
故答案为:60°.
9.3
【解析】∵四边形ABCD是平行四边形,
∴BC=AD=7cm,CD=AB=4cm,CD∥AB,
∴∠F=∠ABF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠F=∠CBF,
∴CF=BC=7cm,
∴DF=CF-CD=7-4=3(cm).
故答案为:3.
10.48
【解析】设BC=x,∵AB+AD=20, 所以BC+CD=20,∴CD=20-x,
∵□ABCD的面积=BC AE=CD AF,∴4x=6(20-x),解得x=12,
∴□ABCD的面积=BC AE=12×4=48,
故答案为:48.
11.(1)证明见解析(2)证明见解析
【解析】(1)根据平行四边形性质得到AB=CD,AB∥CD,再得到∠ABE=∠CDF,根据“有两边和它们的夹角对应相等的两个三角形全等”得到△ABE≌△CDF,据此可得到即可AE=CF;(2)由△ABE≌△CDF可得∠AEB=∠CFD,再根据“等角的补角相等”得到∠AED=∠CFB,再根据“内错角相等,两直线平行”得到AE∥CF即可.
证明:()∵平行四边形
∴,
.
∴.
在和中,
∴≌,
∴
()∵≌,
∴
∴
∴.
12.证明见解析
【解析】(1)要证明AB=CF可通过△AEB≌△FEC证得,利用平行四边形ABCD的性质不难证明;(2)由平行四边形ABCD的性质可得AB=CD,由△AEB≌△FEC可得AB=CF,所以DF=2CF=2AB,所以AD=DF,由等腰三角形三线合一的性质可证得ED⊥AF .
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠F,
∵E是BC的中点,
∴BE=CE,
在△AEB和△FEC中,
,
∴△AEB≌△FEC(AAS),
∴AB=CF;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=CF,DF=DC+CF ,
∴DF=2CF,
∴DF=2AB,
∵AD=2AB,
∴AD=DF,
∵△AEB≌△FEC,
∴AE=EF,
∴ED⊥AF .
