18.1.2 平行四边形的判定 课时 2 同步练习(含解析)
文档属性
| 名称 | 18.1.2 平行四边形的判定 课时 2 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 406.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 10:11:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章《平行四边形》练习
18.1.2平行四边形的判定
第2课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A. 8 B. 10 C. 12 D. 14
第1题图 第2题图 第3题图
2.如图,为测量池塘岸边、两点之间的距离,小亮在池塘的一侧选取一点,测得、的中点、之间的距离是20米,则、两点之间的距离是( ).
A.36米 B.38米 C.40米 D.42米
3.如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
A. 30 B. 15 C. 7.5 D. 45
4.如图,在四边形ABCD 中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=( )
A. 25° B. 30° C. 35° D. 50°
5.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
A. 2 B. 2.5 C. 3 D. 3.5
二、填空题(每小题6分,共30分)
6.如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为_________.
7.如图, ABCD的对角线AC与BD相交于点O,E为BC边中点,已知AB=6cm,则OE的长为__cm.
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=28cm,△OAB的周长是18cm,则EF=_____cm.
第8题图 第9题图 第10题图
9.如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为______cm.
10.如图,四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=35°,则∠PFE的度数是 _________°.
三、解答题(共40分)
11.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.
求证:四边形DFGE是平行四边形.
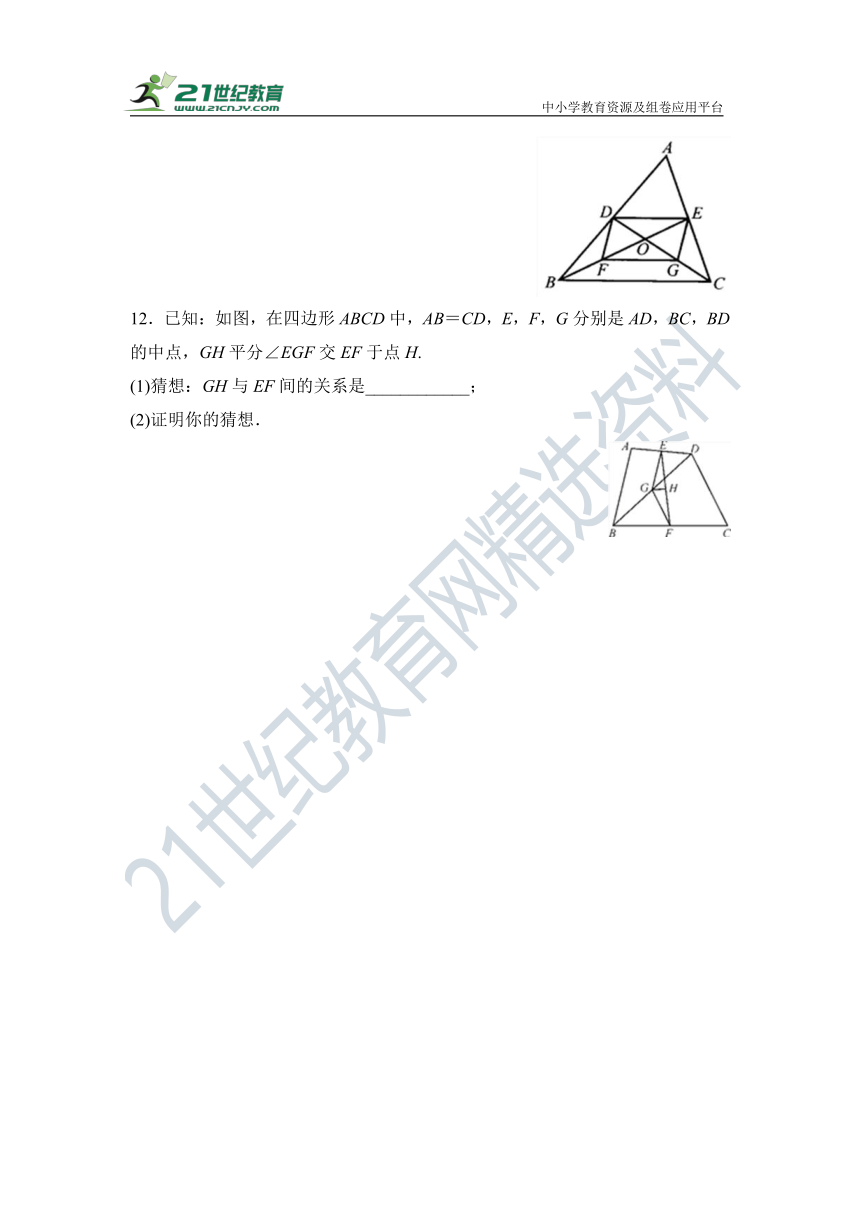
12.已知:如图,在四边形ABCD中,AB=CD,E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.
(1)猜想:GH与EF间的关系是____________;
(2)证明你的猜想.
参考答案
1.C
【解析】试题解析:∵点D. E分别是边AB,BC的中点,
∴DE是三角形BC的中位线,AB=2BD,BC=2BE,
∴DE∥BC且
又∵AB=2BD,BC=2BE,
∴AB+BC+AC=2(BD+BE+DE),
即△ABC的周长是△DBE的周长的2倍,
∵△DBE的周长是6,
∴△ABC的周长是:
6×2=12.
故选C.
2.C
【解析】∵点、是中、边上中点,且,
∴,
∴,
故选.
3.A
【解析】根据三角形中位线的性质可得:AB=2EF,AC=2DF,BC=2DE,则△ABC的周长=2×(EF+DF+DE)=30,故选A.
4.A
【解析】∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN=(180°-∠MPN)÷2=25°,
故选A.
5.C
【解析】如图,延长BN交AC于点D,
因为AN平分∠BAC,BN⊥AN,
所以BN=ND,AD=AB=14,
又因为M是BC的中点,
所以CD=2MN,
因为CD=AC-AD=20-14=6,
所以MN=3,故选C.
6.3
【解析】∵D,E,F分别为△ABC三边的中点,
∴DE∥AF,DF∥EC,DF∥BE且DE=AF,DF=EC,DF=BE,
∴四边形ADEF,DECF,DFEB分别为平行四边形,
故答案为:3.
7.3
【解析】在中,
∵点E是BC的中点,
∴是三角形的中位线,
故答案为:3.
8.2
【解析】∵四边形ABCD是平行四边形,AC+BD=28,
∴AO+BO=14,
又∵OA+OB+AB=18,
∴AB=4,
∵点E、F分别是AO、BO的中点,
∴EF=AB=2(cm).
故答案为:2.
9.9
【解析】因为点A1,B1,C1,D1是四边形ABCD各边上的中点,
所以A1B1=C1D1=BD,A1D1=C1B1=AC,
则四边形A1B1C1D1的周长为AC+BD=5+4=9cm,
故答案为9.
10.35°
【解析】∵四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,
∴PE是△ABD的中位线,PF是△BDC的中位线,
∴PE=AD,PF=BC,
又∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=35°.
故答案为:35°.
11.见解析
【解析】平行四边形的判定方法有多种,选择哪一种解答应先分析题目中给的哪一方面的条件多些,本题中给了两条中位线,利用中位线的性质,可利用一组对边平行且相等来证明.
证明:在△ABC中,∵BE、CD为中线,∴AD=BD,AE=CE,∴DE∥BC且DE=BC.在△OBC中,∵OF=FB,OG=GC,∴FG∥BC且FG=BC,∴DE∥FG,DE=FG,∴四边形DFGE为平行四边形.
12.GH垂直平分EF
【解析】可证明△GEF为等腰三角形,结合条件可证明GH⊥EF.
(1)解:GH⊥EF;
(2)证明:∵G、E分别为BD、AD的中点,
∴GE是△ABD的中位线,
∴GE=AB,
同理可得GF=CD,
又AB=CD,
∴GE=GF,
又∵GH平分∠EGF交EF于点H,
∴GH⊥EF.
第18章《平行四边形》练习
18.1.2平行四边形的判定
第2课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,在△ABC中,点D,E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是( )
A. 8 B. 10 C. 12 D. 14
第1题图 第2题图 第3题图
2.如图,为测量池塘岸边、两点之间的距离,小亮在池塘的一侧选取一点,测得、的中点、之间的距离是20米,则、两点之间的距离是( ).
A.36米 B.38米 C.40米 D.42米
3.如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为( )
A. 30 B. 15 C. 7.5 D. 45
4.如图,在四边形ABCD 中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=( )
A. 25° B. 30° C. 35° D. 50°
5.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
A. 2 B. 2.5 C. 3 D. 3.5
二、填空题(每小题6分,共30分)
6.如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为_________.
7.如图, ABCD的对角线AC与BD相交于点O,E为BC边中点,已知AB=6cm,则OE的长为__cm.
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=28cm,△OAB的周长是18cm,则EF=_____cm.
第8题图 第9题图 第10题图
9.如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为______cm.
10.如图,四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=35°,则∠PFE的度数是 _________°.
三、解答题(共40分)
11.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.
求证:四边形DFGE是平行四边形.
12.已知:如图,在四边形ABCD中,AB=CD,E,F,G分别是AD,BC,BD的中点,GH平分∠EGF交EF于点H.
(1)猜想:GH与EF间的关系是____________;
(2)证明你的猜想.
参考答案
1.C
【解析】试题解析:∵点D. E分别是边AB,BC的中点,
∴DE是三角形BC的中位线,AB=2BD,BC=2BE,
∴DE∥BC且
又∵AB=2BD,BC=2BE,
∴AB+BC+AC=2(BD+BE+DE),
即△ABC的周长是△DBE的周长的2倍,
∵△DBE的周长是6,
∴△ABC的周长是:
6×2=12.
故选C.
2.C
【解析】∵点、是中、边上中点,且,
∴,
∴,
故选.
3.A
【解析】根据三角形中位线的性质可得:AB=2EF,AC=2DF,BC=2DE,则△ABC的周长=2×(EF+DF+DE)=30,故选A.
4.A
【解析】∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AB,PN=DC,
∵AB=CD,
∴PM=PN,
∴△PMN是等腰三角形,
∵∠MPN=130°,
∴∠PMN=(180°-∠MPN)÷2=25°,
故选A.
5.C
【解析】如图,延长BN交AC于点D,
因为AN平分∠BAC,BN⊥AN,
所以BN=ND,AD=AB=14,
又因为M是BC的中点,
所以CD=2MN,
因为CD=AC-AD=20-14=6,
所以MN=3,故选C.
6.3
【解析】∵D,E,F分别为△ABC三边的中点,
∴DE∥AF,DF∥EC,DF∥BE且DE=AF,DF=EC,DF=BE,
∴四边形ADEF,DECF,DFEB分别为平行四边形,
故答案为:3.
7.3
【解析】在中,
∵点E是BC的中点,
∴是三角形的中位线,
故答案为:3.
8.2
【解析】∵四边形ABCD是平行四边形,AC+BD=28,
∴AO+BO=14,
又∵OA+OB+AB=18,
∴AB=4,
∵点E、F分别是AO、BO的中点,
∴EF=AB=2(cm).
故答案为:2.
9.9
【解析】因为点A1,B1,C1,D1是四边形ABCD各边上的中点,
所以A1B1=C1D1=BD,A1D1=C1B1=AC,
则四边形A1B1C1D1的周长为AC+BD=5+4=9cm,
故答案为9.
10.35°
【解析】∵四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,
∴PE是△ABD的中位线,PF是△BDC的中位线,
∴PE=AD,PF=BC,
又∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=35°.
故答案为:35°.
11.见解析
【解析】平行四边形的判定方法有多种,选择哪一种解答应先分析题目中给的哪一方面的条件多些,本题中给了两条中位线,利用中位线的性质,可利用一组对边平行且相等来证明.
证明:在△ABC中,∵BE、CD为中线,∴AD=BD,AE=CE,∴DE∥BC且DE=BC.在△OBC中,∵OF=FB,OG=GC,∴FG∥BC且FG=BC,∴DE∥FG,DE=FG,∴四边形DFGE为平行四边形.
12.GH垂直平分EF
【解析】可证明△GEF为等腰三角形,结合条件可证明GH⊥EF.
(1)解:GH⊥EF;
(2)证明:∵G、E分别为BD、AD的中点,
∴GE是△ABD的中位线,
∴GE=AB,
同理可得GF=CD,
又AB=CD,
∴GE=GF,
又∵GH平分∠EGF交EF于点H,
∴GH⊥EF.
