河北省高碑店市崇德实验中学2022-2023学年高一下学期5月月考数学试题(含解析)
文档属性
| 名称 | 河北省高碑店市崇德实验中学2022-2023学年高一下学期5月月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 874.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 20:16:50 | ||
图片预览




文档简介
崇德实验中学2022-2023学年高一下学期5月月考
数学试题
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.甲、乙去同一家药店各购一种医用外科口罩,已知这家药店出售A,B、C三种医用外科口罩,则甲、乙购买的是同一种医用外科口罩的概率为( )
A. B. C. D.
2.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若向量,满足,,,则与的夹角为( )
A. B. C. D.
4.在三棱锥中,PA、AB、AC两两垂直,,,则三棱锥外接球的表面积为( )
A. B. C. D.
5.已知a,b是两条不同的直线,是平面,且,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分又不必要条件 D.充要条件
6.在《九章算术》中,将四个面都是直角三角形的四面体称作鳖臑.如图,在鳖臑中,平面ABC,是以点B为直角顶点的等腰直角三角形,且,则异面直线BC与SA所成角的大小为( )
A. B. C. D.
7.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,....499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
8.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为,向山顶前进100m到达B处,又测得C对于山坡的斜度为,若,山坡对于地平面的坡度为,则等于( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列事件中,是随机事件的是( )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若,则
10.正方体绕直线旋转之后与其自身重合,则的值可以是( )
A. B.
C. D.
11.如图所示,已知正方体的棱长为2,线段上有两个动点E,F,且,则下列结论中,正确的是( )
A.平面平面
B.存在点E(E与不重合),使得BE与共面
C.当E点运动时,总有
D.三棱锥的体积为定值
12.已知平面,,则下列结论正确的是( )
A. B.
C. D.与的夹角为
三、填空题:本题共4小题,每小题5分,共20分
13.一组数据共40个,分为6组,第1组到第4组的频数分别为10、5、7、6,第5组的频率为0.1,则第6组的频数为______.
14.已知向量,,满足,,,则______.
15.在中,角A,B,C的对边分别为a,b,c,若,则的最小值为______.
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该四棱锥的外接球的体积为______.
四、解答题:本题共6小题,第17题10分,第18-22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知的面积为,且,.
(1)求;
(2)若点D为AB边上一点,且与的面积之比为.
①求证:;②求内切圆的半径r.
18.已知复数(其中且,i为应数单位),且为纯虚数.
(1)求实数a的值;
(2)若,求复数的模.
19.已知向量,.
(1)求与夹角的余弦值;
(2)为何值时,与垂直.
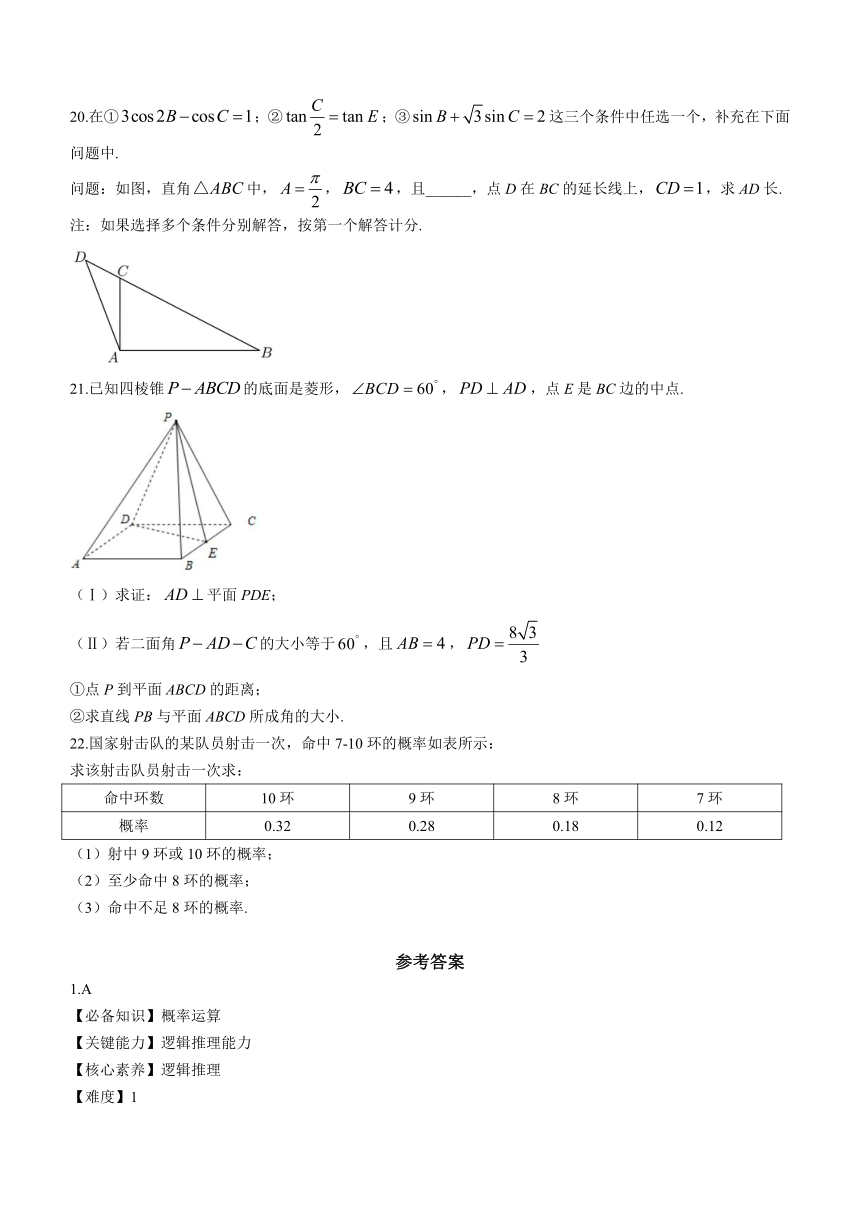
20.在①;②;③这三个条件中任选一个,补充在下面问题中.
问题:如图,直角中,,,且______,点D在BC的延长线上,,求AD长.
注:如果选择多个条件分别解答,按第一个解答计分.
21.已知四棱锥的底面是菱形,,,点E是BC边的中点.
(Ⅰ)求证:平面PDE;
(Ⅱ)若二面角的大小等于,且,
①点P到平面ABCD的距离;
②求直线PB与平面ABCD所成角的大小.
22.国家射击队的某队员射击一次,命中7-10环的概率如表所示:
求该射击队员射击一次求:
命中环数 10环 9环 8环 7环
概率 0.32 0.28 0.18 0.12
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
参考答案
1.A
【必备知识】概率运算
【关键能力】逻辑推理能力
【核心素养】逻辑推理
【难度】1
【解析】甲、乙在A,B,C三种医用外科口罩中各购一种的基本事件有,,,,,,,,共9种,
其中甲,乙购买的是同一种医用外科口罩基本事件有,,3种,
则其概率为.故选:A.
2.D
【必备知识】复数运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:由题意得:
z在复平面上对应的点为,该点在第四象限.故选:D
3.C
【必备知识】向量的加减运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:,,
又,,两向量的夹角的取值范围是,,
.
与的夹角为.故选:C.
4.C
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】由于PA,AB,AC两两垂直,故可得该三棱锥为长方体的一部分,因为外接球半径为长方体体对角线的一半,
所以,
故,故选:C
5.B
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】依题意得,
当,,时,直线a与直线b的位置关系为平行或者异面,
当,,时,由线面平行的判定定理可得,
综上所述,“”是“”的必要不充分条件.故选:B
6.C
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】作正方形ABCD,连接SD,则异面直线BC与SA所成角的平面角为(或其补角),如图所示
由已知有平面ABC,所以,
又因为,,
则面SCD,因为,
所以面SCD,所以,
设,则,,
,则,
所以故选:C.
7.C
【必备知识】随机数表
【关键能力】逻辑推理能力
【核心素养】逻辑推理
【难度】1
【解析】由题意可知,读取的第一个数据是583,不符合条件,第二个数据是921,不符合条件,第三个数据是206,符合条件;
即随机选取的第一袋牛奶标号是206;
以下数据依次是766,301,647,859,169,555,671,998,301,其中符合题意的数据只有301,169,301三个数据,但是301属于重复数据,继续往后计数;
下一个数是071,符合条件,即前四袋牛奶的标号依次为206,301,169,071;
所以,第四袋牛奶的标号为071.故选:C.
8.C
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】在中,由正弦定理得,
.
在中,,
.故选:C
9.AC
【必备知识】随机事件
【关键能力】数学抽象能力
【核心素养】数学抽象
【难度】1
【解析】A选项与C选项为随机事件,B为不可能事件,D为必然事件.
故选:AC.
10.AC
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】解:如图,
正方体中,对角线垂直于平面,且三角形为等边三角形,正方体绕对角线旋转能与原正方体重合.
故选:AC.
11.ACD
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】解:对于A,连接,,BD,,
因为且,所以四边形是平行四边形,所以,
又平面,平面,所以平面,
同理平面,又,,平面AEF,
所以平面平面,故A正确;
对于B,因为平面平面,
平面,平面,,,
若BE与共面,则平面与平面重合,与题意相矛盾,
故不存在点E(E与不重合),使得BE与共面,故B错误;
对于C,连接AC,,则,
因为平面,平面,
所以,又,,平面,
所以平面,又平面,所以,
同理,又,,平面,
所以平面,又平面,
所以,即当E点运动时,总有,故C正确;
对于D,因为平面ABCD,平面ABCD,所以,
又,,,平面,所以平面,
则三棱锥的高为,,
则为定值,故D正确.
故选:ACD.
12.AD
【必备知识】向量的坐标运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】根据向量的坐标运算易知A选项正确;
因为,,所以选项B错误
因为,,所以C错误
因为,所以与的夹角为,D选项正确.
故选:AD.
13.
【必备知识】复数运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】复数,所以.故答案为:
14.
【必备知识】向量的运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】,故①,
,故②,
则①+②得:,所以
故答案为:
15.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:在中,角A,B,C的对边分别为a,b,c,,
当且仅当时,即时取等号,
的最小值为.
16.
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】取AB的中点O,连接OD,1.
由题可知正方形ABCD的中心即为球心,
设球半径为r,则,
,
解得,
该四棱锥的外接球的体积为.
故答案为:.
17.(1);(2)①证明见解析;②.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】(1)的面积为,,
由余弦定理得,,
由余弦定理得
(2)①与的面积之比为,,
由余弦定理得,
,即
②(法一)在中,
(法二)设的周长为C,由得
18.(1)(2)
【必备知识】复数的运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】(1)
由已知得:,且是纯虚数
,,.
(2)由(1)得:,
.
19.(1)(2)
【必备知识】向量运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】
(1)解:由题意可得,,
,设与夹角为,
,即与夹角的余弦值为.
(2)解:因为,,所以,
与垂直,
所以,解得.
20.条件选择见解析:.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】选①直角中,
即,得,
,且
,.
选②直角中,
,得
,
,且
,
选③直角中,
,
,
,且
,.
21.(1)证明见解析;(Ⅱ)①4,②.
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】(1)连接BD,底面ABCD是菱形,,
是正三角形.
点E是BC边的中点,,
,.,,
平面PDE;
(Ⅱ)①,,
为二面角的平面角,,
过P在平面PDE内做于K,由(1)易.
面ABCD.
,,,
即点P到平面ABCD的距离是4.
②,,,K为重心.
连接BK,为正三角形,所以BK为BP在面ABCD内的射影.
,为直线PB与平面ABCD所成角,
中,,,
直线PB与平面ABCD所成角的大小为.
22.(1)0.6;(2)0.78;(3)0.22.
【必备知识】概率
【关键能力】数学抽象能力、数据分析能力
【核心素养】数学抽象、数据分析
【难度】1
【解析】
记事件“射击一次,命中k环”为,则事件彼此互斥.
(1)记“射击一次,射中9环或10环”为事件A,那么当,之一发生时,事件A发生,由互斥事件的加法公式得
(2)设“射击一次,至少命中8环”的事件为B,那么当,,之一发生时,事件B发生.由互斥事件概率的加法公式得
(3)由于事件“射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件:即B表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
点睛:互斥事件概率加法公式:若A,B互斥,则,独立事件概率乘法公式:若A,B相互独立,则.
数学试题
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.甲、乙去同一家药店各购一种医用外科口罩,已知这家药店出售A,B、C三种医用外科口罩,则甲、乙购买的是同一种医用外科口罩的概率为( )
A. B. C. D.
2.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若向量,满足,,,则与的夹角为( )
A. B. C. D.
4.在三棱锥中,PA、AB、AC两两垂直,,,则三棱锥外接球的表面积为( )
A. B. C. D.
5.已知a,b是两条不同的直线,是平面,且,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.既不充分又不必要条件 D.充要条件
6.在《九章算术》中,将四个面都是直角三角形的四面体称作鳖臑.如图,在鳖臑中,平面ABC,是以点B为直角顶点的等腰直角三角形,且,则异面直线BC与SA所成角的大小为( )
A. B. C. D.
7.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,....499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
8.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为,向山顶前进100m到达B处,又测得C对于山坡的斜度为,若,山坡对于地平面的坡度为,则等于( )
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列事件中,是随机事件的是( )
A.2021年8月18日,北京市不下雨
B.在标准大气压下,水在时结冰
C.从标有1,2,3,4的4张号签中任取一张,恰为1号签
D.若,则
10.正方体绕直线旋转之后与其自身重合,则的值可以是( )
A. B.
C. D.
11.如图所示,已知正方体的棱长为2,线段上有两个动点E,F,且,则下列结论中,正确的是( )
A.平面平面
B.存在点E(E与不重合),使得BE与共面
C.当E点运动时,总有
D.三棱锥的体积为定值
12.已知平面,,则下列结论正确的是( )
A. B.
C. D.与的夹角为
三、填空题:本题共4小题,每小题5分,共20分
13.一组数据共40个,分为6组,第1组到第4组的频数分别为10、5、7、6,第5组的频率为0.1,则第6组的频数为______.
14.已知向量,,满足,,,则______.
15.在中,角A,B,C的对边分别为a,b,c,若,则的最小值为______.
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥,该四棱锥的体积为,则该四棱锥的外接球的体积为______.
四、解答题:本题共6小题,第17题10分,第18-22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知的面积为,且,.
(1)求;
(2)若点D为AB边上一点,且与的面积之比为.
①求证:;②求内切圆的半径r.
18.已知复数(其中且,i为应数单位),且为纯虚数.
(1)求实数a的值;
(2)若,求复数的模.
19.已知向量,.
(1)求与夹角的余弦值;
(2)为何值时,与垂直.
20.在①;②;③这三个条件中任选一个,补充在下面问题中.
问题:如图,直角中,,,且______,点D在BC的延长线上,,求AD长.
注:如果选择多个条件分别解答,按第一个解答计分.
21.已知四棱锥的底面是菱形,,,点E是BC边的中点.
(Ⅰ)求证:平面PDE;
(Ⅱ)若二面角的大小等于,且,
①点P到平面ABCD的距离;
②求直线PB与平面ABCD所成角的大小.
22.国家射击队的某队员射击一次,命中7-10环的概率如表所示:
求该射击队员射击一次求:
命中环数 10环 9环 8环 7环
概率 0.32 0.28 0.18 0.12
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
参考答案
1.A
【必备知识】概率运算
【关键能力】逻辑推理能力
【核心素养】逻辑推理
【难度】1
【解析】甲、乙在A,B,C三种医用外科口罩中各购一种的基本事件有,,,,,,,,共9种,
其中甲,乙购买的是同一种医用外科口罩基本事件有,,3种,
则其概率为.故选:A.
2.D
【必备知识】复数运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:由题意得:
z在复平面上对应的点为,该点在第四象限.故选:D
3.C
【必备知识】向量的加减运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:,,
又,,两向量的夹角的取值范围是,,
.
与的夹角为.故选:C.
4.C
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】由于PA,AB,AC两两垂直,故可得该三棱锥为长方体的一部分,因为外接球半径为长方体体对角线的一半,
所以,
故,故选:C
5.B
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】依题意得,
当,,时,直线a与直线b的位置关系为平行或者异面,
当,,时,由线面平行的判定定理可得,
综上所述,“”是“”的必要不充分条件.故选:B
6.C
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】作正方形ABCD,连接SD,则异面直线BC与SA所成角的平面角为(或其补角),如图所示
由已知有平面ABC,所以,
又因为,,
则面SCD,因为,
所以面SCD,所以,
设,则,,
,则,
所以故选:C.
7.C
【必备知识】随机数表
【关键能力】逻辑推理能力
【核心素养】逻辑推理
【难度】1
【解析】由题意可知,读取的第一个数据是583,不符合条件,第二个数据是921,不符合条件,第三个数据是206,符合条件;
即随机选取的第一袋牛奶标号是206;
以下数据依次是766,301,647,859,169,555,671,998,301,其中符合题意的数据只有301,169,301三个数据,但是301属于重复数据,继续往后计数;
下一个数是071,符合条件,即前四袋牛奶的标号依次为206,301,169,071;
所以,第四袋牛奶的标号为071.故选:C.
8.C
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】在中,由正弦定理得,
.
在中,,
.故选:C
9.AC
【必备知识】随机事件
【关键能力】数学抽象能力
【核心素养】数学抽象
【难度】1
【解析】A选项与C选项为随机事件,B为不可能事件,D为必然事件.
故选:AC.
10.AC
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】解:如图,
正方体中,对角线垂直于平面,且三角形为等边三角形,正方体绕对角线旋转能与原正方体重合.
故选:AC.
11.ACD
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】解:对于A,连接,,BD,,
因为且,所以四边形是平行四边形,所以,
又平面,平面,所以平面,
同理平面,又,,平面AEF,
所以平面平面,故A正确;
对于B,因为平面平面,
平面,平面,,,
若BE与共面,则平面与平面重合,与题意相矛盾,
故不存在点E(E与不重合),使得BE与共面,故B错误;
对于C,连接AC,,则,
因为平面,平面,
所以,又,,平面,
所以平面,又平面,所以,
同理,又,,平面,
所以平面,又平面,
所以,即当E点运动时,总有,故C正确;
对于D,因为平面ABCD,平面ABCD,所以,
又,,,平面,所以平面,
则三棱锥的高为,,
则为定值,故D正确.
故选:ACD.
12.AD
【必备知识】向量的坐标运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】根据向量的坐标运算易知A选项正确;
因为,,所以选项B错误
因为,,所以C错误
因为,所以与的夹角为,D选项正确.
故选:AD.
13.
【必备知识】复数运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】复数,所以.故答案为:
14.
【必备知识】向量的运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】,故①,
,故②,
则①+②得:,所以
故答案为:
15.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】解:在中,角A,B,C的对边分别为a,b,c,,
当且仅当时,即时取等号,
的最小值为.
16.
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】取AB的中点O,连接OD,1.
由题可知正方形ABCD的中心即为球心,
设球半径为r,则,
,
解得,
该四棱锥的外接球的体积为.
故答案为:.
17.(1);(2)①证明见解析;②.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】(1)的面积为,,
由余弦定理得,,
由余弦定理得
(2)①与的面积之比为,,
由余弦定理得,
,即
②(法一)在中,
(法二)设的周长为C,由得
18.(1)(2)
【必备知识】复数的运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】(1)
由已知得:,且是纯虚数
,,.
(2)由(1)得:,
.
19.(1)(2)
【必备知识】向量运算
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】
(1)解:由题意可得,,
,设与夹角为,
,即与夹角的余弦值为.
(2)解:因为,,所以,
与垂直,
所以,解得.
20.条件选择见解析:.
【必备知识】解三角形
【关键能力】数学运算能力
【核心素养】数学运算
【难度】1
【解析】选①直角中,
即,得,
,且
,.
选②直角中,
,得
,
,且
,
选③直角中,
,
,
,且
,.
21.(1)证明见解析;(Ⅱ)①4,②.
【必备知识】空间立体几何
【关键能力】空间想象能力
【核心素养】空间想象
【难度】1
【解析】(1)连接BD,底面ABCD是菱形,,
是正三角形.
点E是BC边的中点,,
,.,,
平面PDE;
(Ⅱ)①,,
为二面角的平面角,,
过P在平面PDE内做于K,由(1)易.
面ABCD.
,,,
即点P到平面ABCD的距离是4.
②,,,K为重心.
连接BK,为正三角形,所以BK为BP在面ABCD内的射影.
,为直线PB与平面ABCD所成角,
中,,,
直线PB与平面ABCD所成角的大小为.
22.(1)0.6;(2)0.78;(3)0.22.
【必备知识】概率
【关键能力】数学抽象能力、数据分析能力
【核心素养】数学抽象、数据分析
【难度】1
【解析】
记事件“射击一次,命中k环”为,则事件彼此互斥.
(1)记“射击一次,射中9环或10环”为事件A,那么当,之一发生时,事件A发生,由互斥事件的加法公式得
(2)设“射击一次,至少命中8环”的事件为B,那么当,,之一发生时,事件B发生.由互斥事件概率的加法公式得
(3)由于事件“射击一次,命中不足8环”是事件B:“射击一次,至少命中8环”的对立事件:即B表示事件“射击一次,命中不足8环”,根据对立事件的概率公式得
点睛:互斥事件概率加法公式:若A,B互斥,则,独立事件概率乘法公式:若A,B相互独立,则.
同课章节目录
