11.1.2 构成空间几何体的基本元素(含解析)
文档属性
| 名称 | 11.1.2 构成空间几何体的基本元素(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览

文档简介
课时作业(九) 构成空间几何体的基本元素
一、选择题
1.如图所示的是平行四边形ABCD所在的平面,有下列表示方法:①平面ABCD;②平面BD;③平面AD;④平面ABC;⑤AC;⑥平面α.其中不正确的是( )
A.④⑤ B.③④⑤
C.②③④⑤ D.③⑤
2.若直线a不平行于平面α,则下列结论成立的是( )
A.α内的所有直线均与a异面
B.α内不存在与a平行的直线
C.α内直线均与a相交
D.直线a与平面α有公共点
3.已知a,b为两条不同的直线,α,β为两个不同的平面,α∩β=a,a∥b,则下面结论不可能成立的是( )
A.b β,且b∥α
B.b α
C.b∥α,且b∥β
D.b与α,β都相交
4.能正确表示点A在直线l上且直线l在平面α内的是( )
二、填空题
5.线段AB长为5 cm,在水平面上向右移动4 cm后记为CD,将CD沿铅垂线方向向下移动3 cm后记为C′D′,再将C′D′沿水平方向向左移动4 cm后记为A′B′,依次连接构成长方体ABCD A′B′C′D′.
(1)该长方体的高为________cm;
(2)平面A′B′BA与平面CDD′C′间的距离为________cm;
(3)点A到平面BCC′B′的距离为______cm.
6.过三棱柱ABC A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.
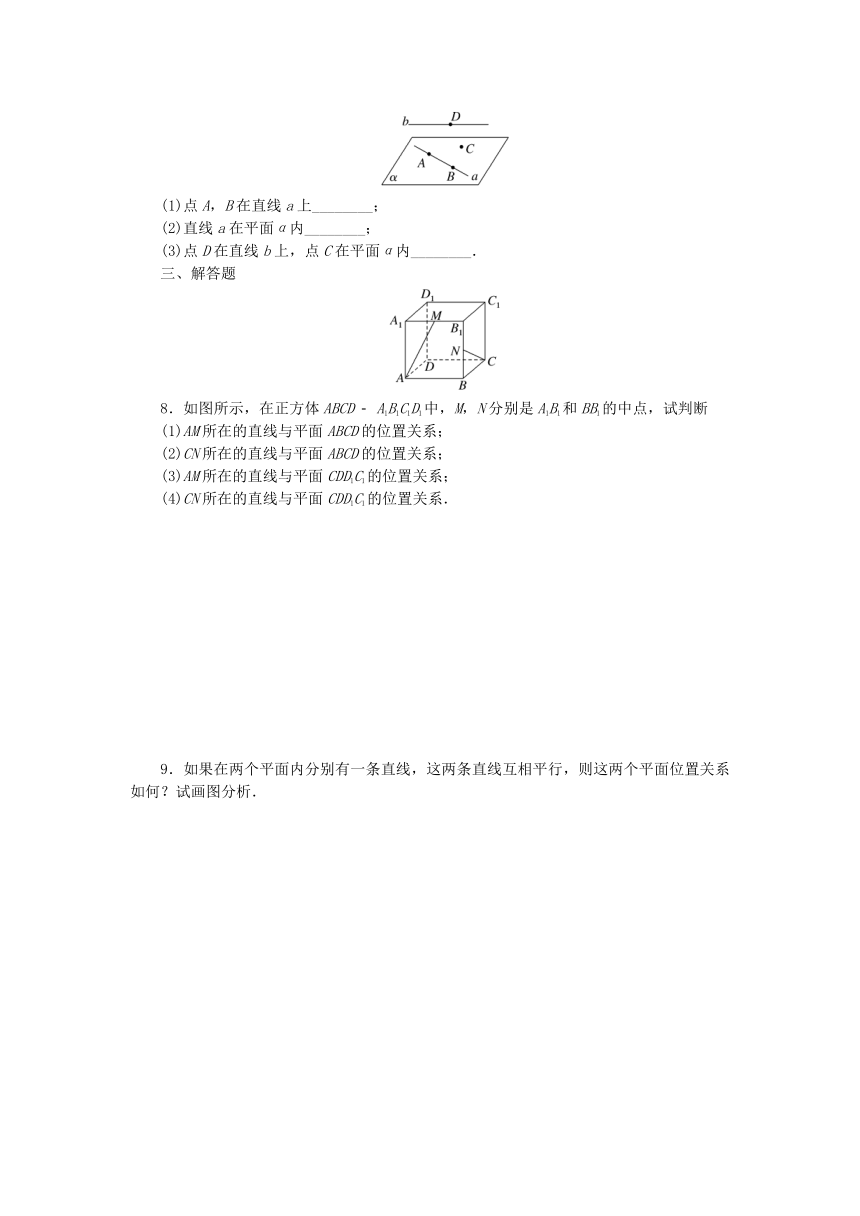
7.如图所示,用符号语言表示以下各概念:
(1)点A,B在直线a上________;
(2)直线a在平面α内________;
(3)点D在直线b上,点C在平面α内________.
三、解答题
8.如图所示,在正方体ABCD A1B1C1D1中,M,N分别是A1B1和BB1的中点,试判断
(1)AM所在的直线与平面ABCD的位置关系;
(2)CN所在的直线与平面ABCD的位置关系;
(3)AM所在的直线与平面CDD1C1的位置关系;
(4)CN所在的直线与平面CDD1C1的位置关系.
9.如果在两个平面内分别有一条直线,这两条直线互相平行,则这两个平面位置关系如何?试画图分析.
[尖子生题库]
10.(1)若空间三个平面两两相交,则它们的交线条数是( )
A.1或2 B.2或3
C.1或3 D.1或2或3
(2)下列说法错误的是( )
A.若直线l平行于平面α,则平面α内存在直线与l平行
B.若直线l平行于平面α,则平面α内存在直线与l异面
C.若直线l平行于平面α,则平面α内存在直线与l垂直
D.若直线l平行于平面α,则平面α内存在直线与l相交
(3)下列命题中正确的个数为( )
①书桌面是平面;②9个平面重叠起来,要比7个平面重叠起来厚;③有一个平面的长是50 m,宽是20 m;④平面是绝对平的、无厚度的、可以无限延展的抽象的数学概念.
A.1 B.2
C.3 D.4
课时作业(九) 构成空间几何体的基本元素
1.解析:③中AD不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
答案:D
2.解析:由于直线a不平行于平面α,则a在α内或a与α相交,故A错;当a α时,在平面α内存在与a平行的直线,故B错;因为α内的直线也可能与a平行或异面,故C错;由线面平行的定义知D正确.
答案:D
3.解析:由a,b为两条不同的直线,α,β为两个不同的平面,α∩β=a,a∥b,知:对于选项A,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1 平面ABCD,C1D1∥AB,此时有C1D1 平面ABB1A1,C1D1∥平面ABCD成立,故排除A.
对于选项B,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1∥平面ABCD,且C1D1∥平面ABB1A1,所以b α有可能成立,故排除B;对于选项C ,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1∥平面ABCD,且C1D1∥平面ABB1A1,所以b∥α,且b∥β有可能成立,故排除C;对于选项D,b与α,β都相交不可能成立.
答案:D
4.解析:选项A只表示点A在直线l上;选项D表示直线l与平面α相交于点A;选项B中的直线l有部分在平行四边形的外面,所以不能表示直线在平面α内,故选C.
答案:C
5.解析:如图,
在长方体ABCD A′B′C′D′中,AB=5 cm,BC=4 cm,CC′=3 cm,
∴长方体的高为3 cm;平面A′B′BA与平面CDD′C′之间的距离为4 cm;点A到平面BCC′B′的距离为5 cm.
答案:(1)3 (2)4 (3)5
6.解析:如图所示,与平面ABB1A1平行的直线有6条:D1E1,E1E,ED,DD1,D1E,DE1.
答案:6
7.解析:根据点、线、面位置关系及其表示方法可知:
(1)A∈a,B∈a,(2)a α,(3)D∈b,C∈α.
答案:(1)A∈a,B∈a (2)a α (3)D∈b,C∈α
8.解析:(1)AM所在的直线与平面ABCD相交.
(2)CN所在的直线与平面ABCD相交.
(3)AM所在的直线与平面CDD1C1平行.
(4)CN所在的直线与平面CDD1C1相交.
9.解析:这两个平面平行(如图①)或相交(如图②).
10.解析:(1)若三个平面经过同一条直线,则有1条交线;若三个平面不过同一条直线,则有3条交线.
(2)若直线l平行于平面α,则平面α内的直线与l平行或异面,故A,B正确;
在C中,若直线l平行于平面α,则平面α内存在直线与l异面垂直,故C正确;
在D中,若直线l平行于平面α,则平面α内的直线与l平行或异面,故D错误.
(3)由平面的概念知,只有④正确.
答案:(1)C (2)D (3)A
一、选择题
1.如图所示的是平行四边形ABCD所在的平面,有下列表示方法:①平面ABCD;②平面BD;③平面AD;④平面ABC;⑤AC;⑥平面α.其中不正确的是( )
A.④⑤ B.③④⑤
C.②③④⑤ D.③⑤
2.若直线a不平行于平面α,则下列结论成立的是( )
A.α内的所有直线均与a异面
B.α内不存在与a平行的直线
C.α内直线均与a相交
D.直线a与平面α有公共点
3.已知a,b为两条不同的直线,α,β为两个不同的平面,α∩β=a,a∥b,则下面结论不可能成立的是( )
A.b β,且b∥α
B.b α
C.b∥α,且b∥β
D.b与α,β都相交
4.能正确表示点A在直线l上且直线l在平面α内的是( )
二、填空题
5.线段AB长为5 cm,在水平面上向右移动4 cm后记为CD,将CD沿铅垂线方向向下移动3 cm后记为C′D′,再将C′D′沿水平方向向左移动4 cm后记为A′B′,依次连接构成长方体ABCD A′B′C′D′.
(1)该长方体的高为________cm;
(2)平面A′B′BA与平面CDD′C′间的距离为________cm;
(3)点A到平面BCC′B′的距离为______cm.
6.过三棱柱ABC A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.
7.如图所示,用符号语言表示以下各概念:
(1)点A,B在直线a上________;
(2)直线a在平面α内________;
(3)点D在直线b上,点C在平面α内________.
三、解答题
8.如图所示,在正方体ABCD A1B1C1D1中,M,N分别是A1B1和BB1的中点,试判断
(1)AM所在的直线与平面ABCD的位置关系;
(2)CN所在的直线与平面ABCD的位置关系;
(3)AM所在的直线与平面CDD1C1的位置关系;
(4)CN所在的直线与平面CDD1C1的位置关系.
9.如果在两个平面内分别有一条直线,这两条直线互相平行,则这两个平面位置关系如何?试画图分析.
[尖子生题库]
10.(1)若空间三个平面两两相交,则它们的交线条数是( )
A.1或2 B.2或3
C.1或3 D.1或2或3
(2)下列说法错误的是( )
A.若直线l平行于平面α,则平面α内存在直线与l平行
B.若直线l平行于平面α,则平面α内存在直线与l异面
C.若直线l平行于平面α,则平面α内存在直线与l垂直
D.若直线l平行于平面α,则平面α内存在直线与l相交
(3)下列命题中正确的个数为( )
①书桌面是平面;②9个平面重叠起来,要比7个平面重叠起来厚;③有一个平面的长是50 m,宽是20 m;④平面是绝对平的、无厚度的、可以无限延展的抽象的数学概念.
A.1 B.2
C.3 D.4
课时作业(九) 构成空间几何体的基本元素
1.解析:③中AD不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
答案:D
2.解析:由于直线a不平行于平面α,则a在α内或a与α相交,故A错;当a α时,在平面α内存在与a平行的直线,故B错;因为α内的直线也可能与a平行或异面,故C错;由线面平行的定义知D正确.
答案:D
3.解析:由a,b为两条不同的直线,α,β为两个不同的平面,α∩β=a,a∥b,知:对于选项A,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1 平面ABCD,C1D1∥AB,此时有C1D1 平面ABB1A1,C1D1∥平面ABCD成立,故排除A.
对于选项B,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1∥平面ABCD,且C1D1∥平面ABB1A1,所以b α有可能成立,故排除B;对于选项C ,在正方体ABCD A1B1C1D1中,平面ABCD∩平面ABB1A1=AB,C1D1∥平面ABCD,且C1D1∥平面ABB1A1,所以b∥α,且b∥β有可能成立,故排除C;对于选项D,b与α,β都相交不可能成立.
答案:D
4.解析:选项A只表示点A在直线l上;选项D表示直线l与平面α相交于点A;选项B中的直线l有部分在平行四边形的外面,所以不能表示直线在平面α内,故选C.
答案:C
5.解析:如图,
在长方体ABCD A′B′C′D′中,AB=5 cm,BC=4 cm,CC′=3 cm,
∴长方体的高为3 cm;平面A′B′BA与平面CDD′C′之间的距离为4 cm;点A到平面BCC′B′的距离为5 cm.
答案:(1)3 (2)4 (3)5
6.解析:如图所示,与平面ABB1A1平行的直线有6条:D1E1,E1E,ED,DD1,D1E,DE1.
答案:6
7.解析:根据点、线、面位置关系及其表示方法可知:
(1)A∈a,B∈a,(2)a α,(3)D∈b,C∈α.
答案:(1)A∈a,B∈a (2)a α (3)D∈b,C∈α
8.解析:(1)AM所在的直线与平面ABCD相交.
(2)CN所在的直线与平面ABCD相交.
(3)AM所在的直线与平面CDD1C1平行.
(4)CN所在的直线与平面CDD1C1相交.
9.解析:这两个平面平行(如图①)或相交(如图②).
10.解析:(1)若三个平面经过同一条直线,则有1条交线;若三个平面不过同一条直线,则有3条交线.
(2)若直线l平行于平面α,则平面α内的直线与l平行或异面,故A,B正确;
在C中,若直线l平行于平面α,则平面α内存在直线与l异面垂直,故C正确;
在D中,若直线l平行于平面α,则平面α内的直线与l平行或异面,故D错误.
(3)由平面的概念知,只有④正确.
答案:(1)C (2)D (3)A
