青岛版数学七年级下册第9章 平行线 单元复习测试题(含解析)
文档属性
| 名称 | 青岛版数学七年级下册第9章 平行线 单元复习测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 726.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 08:44:21 | ||
图片预览



文档简介
青岛版七年级下册第9章 平行线单元测试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,和属于同位角的有( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
2.下列说法中,正确的是( )
A.平面内,没有公共点的两条线段平行
B.平面内,没有公共点的两条射线平行
C.没有公共点的两条直线互相平行
D.互相平行的两条直线没有公共点
3.如图,下列能判定∥的条件有几个( )
(1) (2)(3) (4).
A.4 B.3 C.2 D.1
4.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
5.如图,将一副三角板按如图所示的方式摆放,其中两条斜边,角的顶点与含角的直角三角板的直角顶点重合,点,,在同一条直线上,则的为( )
A. B. C. D.
6.如图,,平分交于点E,若,则 ( )
A. B. C. D.
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的度数是( )
A. B. C. D.
8.如图, ,,,则( )
A. B. C. D.
二、多选题
9.如图所示,下列说法中正确的是( )
A.与是同旁内角; B.与是内错角;
C.与是内错角; D.与是同位角.
10.下列说法正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
11.如图,如果,,则下列结论正确的为( )
A. B. C.平分 D.
12.如图,点P在直线m上移动,A,B是直线n上的两个定点,且直线.对于下列各值,不会随点P的移动而变化的是( )
A.点P到直线n的距离 B.的周长
C.的面积 D.的大小
三、填空题
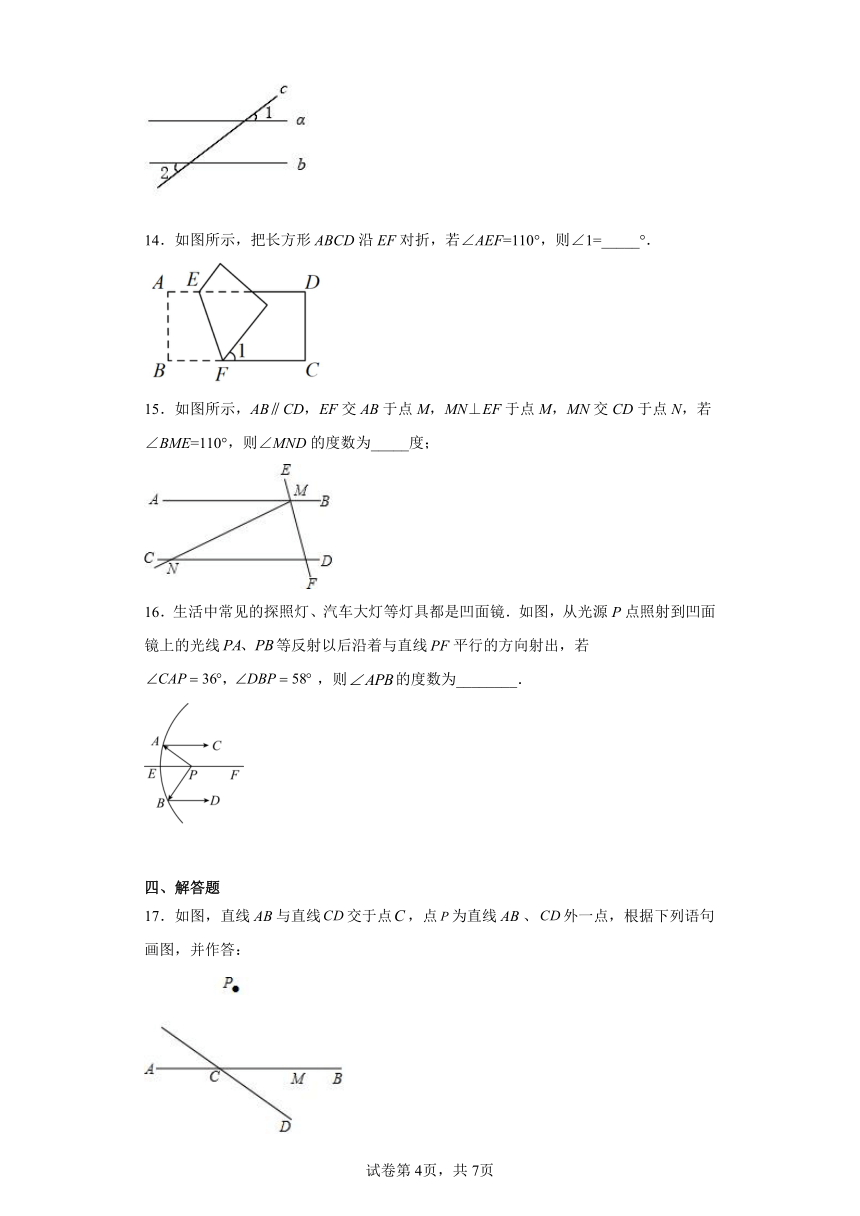
13.如图,,,则∠2等于______.
14.如图所示,把长方形ABCD沿EF对折,若∠AEF=110°,则∠1=_____°.
15.如图所示,ABCD,EF交AB于点M,MN⊥EF于点M,MN交CD于点N,若∠BME=110°,则∠MND的度数为_____度;
16.生活中常见的探照灯、汽车大灯等灯具都是凹面镜.如图,从光源P点照射到凹面镜上的光线等反射以后沿着与直线平行的方向射出,若,则的度数为________.
四、解答题
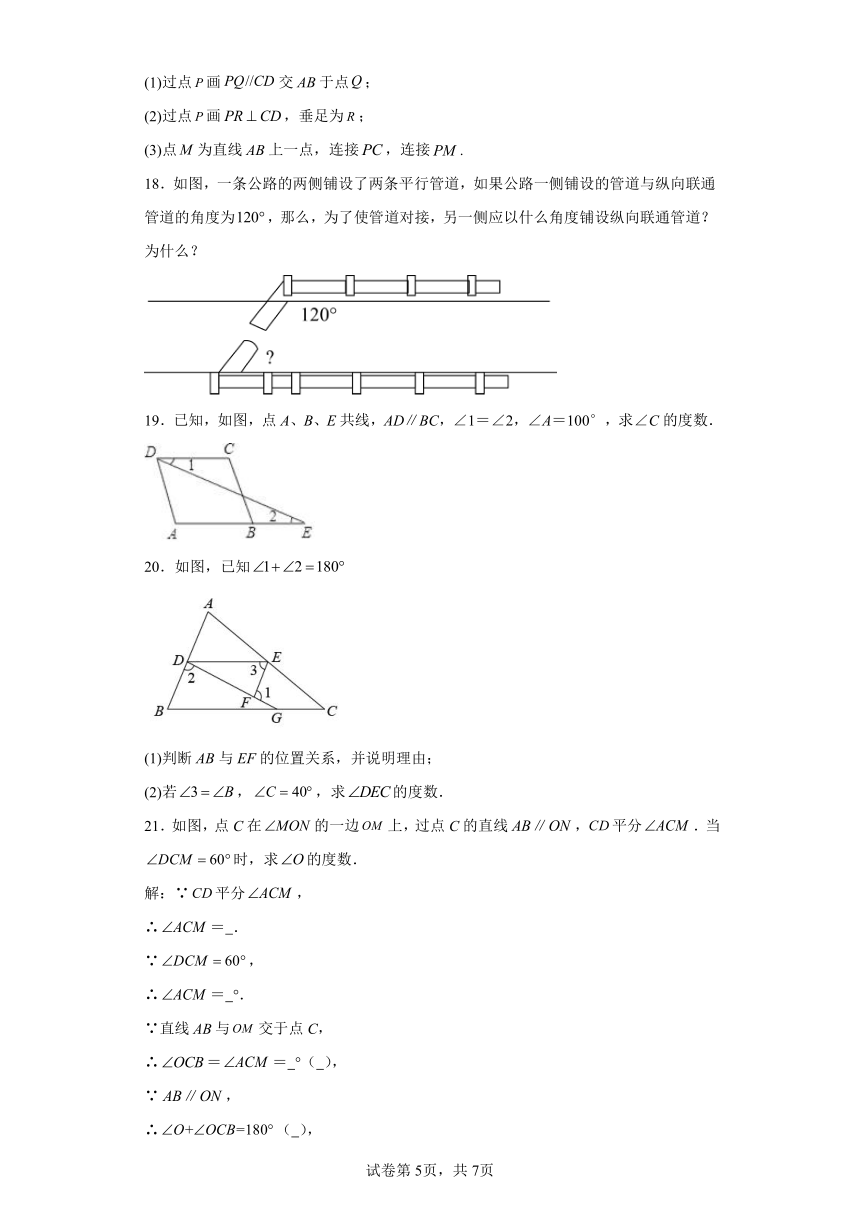
17.如图,直线与直线交于点,点为直线、外一点,根据下列语句画图,并作答:
(1)过点画交于点;
(2)过点画,垂足为;
(3)点为直线上一点,连接,连接.
18.如图,一条公路的两侧铺设了两条平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为,那么,为了使管道对接,另一侧应以什么角度铺设纵向联通管道?为什么?
19.已知,如图,点A、B、E共线,AD∥BC,∠1=∠2,∠A=100°,求∠C的度数.
20.如图,已知
(1)判断AB与EF的位置关系,并说明理由;
(2)若,,求的度数.
21.如图,点C在的一边上,过点C的直线,平分.当时,求的度数.
解:∵平分,
∴= .
∵,
∴= °.
∵直线与交于点C,
∴== °( ),
∵,
∴( ),
∴= °.
22.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中∠A=60°,∠B=45°.
(1)如图1,若∠DCE=40°,则∠ACE= .∠ACB= .
(2)由(1)猜想∠ACB和∠DCE的数量关系,并证明你的结论:
(3)若固定△ACD,将△BCE绕点C旋转.
①如图2,当旋转至BEAC时,则∠ACE= .
②如图3,当旋转至BCAD时,则∠ACE= .
23.已知,定点,分别在直线,上,在平行线,之间有一动点.
(1)如图1所示时,试问,,满足怎样的数量关系 并说明理由.
(2)除了(1)的结论外,试问,,还可能满足怎样的数量关系 请画图并证明
(3)当满足,且,分别平分和,
①若,则__________°.
②猜想与的数量关系.(直接写出结论)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】同位角的定义是两条直线被第三条直线所截时,在截线的同旁,被截两条直线的同一侧的角,简单记忆为F形的两个角,很明显选①②⑤.
【详解】依据同位角的定义可以看出③的两个角并不是由3条线截取得到的,④中的而两个角不在截线的同旁,所以都不能选,①②⑤都符合条件.
【点睛】本题考查同位角的定义,能够熟记模型并运用模型进行判断是解题关键.
2.D
【分析】回忆线段之间、射线之间与直线之间的位置关系;对于A,可在纸上画出两条没有公共点的线段,观察两条线段的位置关系;对于B,可在纸上画出两条没有公共点的射线,观察两条线段的位置关系;对于C,思考若两条直线不在一个平面内,是否能够得到两条直线不平行也不相交,对于D,根据平行线的定义可作出判断.
【详解】对于A,如图所示,A错误;
对于B,如图所示,B错误;
对于C,如果两条直线不在同一个平面内,不相交也可能不平行,则C错误;
对于D,根据平行线的定义可知D正确.
故答案为D.
【点睛】本题考查了两条直线的位置关系,直线、射线、线段的定义,熟练掌握直线的位置关系及相关定义是本题解题的关键.
3.B
【分析】根据平行线的判定逐一判定即可.
【详解】因为,所有AD∥BC,故(1)错误.
因为,所以∥,故(2)正确.
因为,所以∥,故(3)正确.
因为,所以∥,故(4)正确.
所以共有3个正确条件.
故选B
【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.
4.C
【分析】根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.观察各个选项中角的数量关系(相等或互补)、位置关系是否符合上述三个定理,即可判断所给选项是否正确.
【详解】A. 因为和是同旁内角,所以根据不能得到,故A选项错误;
B. 因为和不是同位角也不是内错角,所以根据不能得到,故B选项错误;
C. 因为和是同旁内角,所以根据可以得到,故本选项正确;
D. 和虽然是同位角,但根据只可以得出,故本选项错误.
故本题选C.
【点睛】本题考查平行线的判定定理,在这里①判断两条直线是否平行,是根据角的数量关系(相等或互补)和位置关系去判定的,只有同时满足两种关系,才可根据定理判断平行;②完整的定理前面有一句两直线被第三条直线所截,找准截线和被截线很关键(例如D选项和是同位角,它们的被截线是AB和DE).
5.A
【分析】由题意得∠ADE=45°,∠BAC=30°,由平行线的性质得出∠BAD=∠ADE=45°,即可得出答案.
【详解】解:由题意得:∠ADE=45°,∠BAC=30°,
∵AB∥DE,
∴∠BAD=∠ADE=45°,
∴∠CAD=∠BAD-∠BAC=45°-30°=15°;
故选:A.
【点睛】本题考查了直角三角形的性质、平行线的性质等知识;熟练掌握平行线的性质是解题的关键.
6.A
【分析】如图:根据平角的定义及角平分线的性质求得的度数,再根据平行线的性质求解即可.
【详解】解:如图:
∵,
∴,
∵平分
∴,
∵,
∴,
∴.
故选:A.
【点睛】本题主要考查了平行线的性质、角平分线的定义等知识点,灵活运用平行线的性质是解答本题的关键.
7.B
【分析】根据平行线的性质即可求解.
【详解】解:延长BC至G,如下图所示,
由题意得,AF∥BE,AD∥BC,
∵AF∥BE,
∴∠1=∠3(两直线平行,同位角相等),
∵AD∥BC,
∴∠3=∠4(两直线平行,同位角相等),
∴∠4=∠1=40°,
∵CD∥BE,
∴∠6=∠4=40°(两直线平行,同位角相等),
∵这条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,
∴∠5=∠6=40°,
∴∠2=180°-∠5-∠6=180°-40°-40°=100°,
故选:B.
【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.
8.D
【分析】过点作,根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等得出,然后整理即可得解.
【详解】过点作,
(两直线平行,内错角相等),
,
(已知),
(平行于同一直线的两直线平行),
(两直线平行,同旁内角互补),
,
.
故选:D.
【点睛】本题考查了平行线的判定与性质,作辅助线构造出平行线是解题的关键.
9.ABD
【分析】根据同位角的定义:两条直线被第三条直线所截,在截线的同旁,被截两直线的同一侧的角叫做同位角;内错角的定义,两个角分别在截线的两侧,且在两条被截线之间,具有这样位置关系的一对角叫做内错角;同旁内角的定义:两条直线被第三条直线所截,在截线的同旁,且在被截的两条直线之内的两角,叫做同旁内角,进行逐一判断即可.
【详解】解:根据内错角、同旁内角和同位角的定义可知:A、B、D均是正确的符合题意,∠A与∠C是同旁内角,C不符合题意.
故选ABD.
【点睛】本题考查的知识点是同位角,内错角,同旁内角的概念,解题关键是熟记内错角、同旁内角和同位角的定义.
10.BCD
【分析】根据平行线的定义及平行公理进行判断.
【详解】A. 若点在直线上,则不可以作出已知直线的平行线,因此 “过任意一点可作已知直线的一条平行线”说法错误;
B. “同一平面内两条不相交的直线是平行线”说法正确;
C. “在同一平面内,过直线外一点只能画一条直线与已知直线垂直”说法正确;
D. “平行于同一直线的两直线平行”说法正确;
故选BCD.
【点睛】本题主要考查平行线的定义及平行公理,熟练掌握公理、定理是解决本题的关键.
11.ABD
【分析】根据平行线的性质和判定进行解题即可.
【详解】解:∵DE∥BC,
∴∠DCB=∠1,∠AED=∠ACB,故B符合题意;
∵∠1=∠2,
∴∠2=∠DCB,
∴FG∥DC,故A符合题意;
∴∠BFG=∠BDC,
又∵∠BDC+∠ADC=180°,
∴∠BFG+∠ADC=180°,故D符合题意;
∵∠BCD≠∠ACD,
∴CD平分∠ACB是错误的,故C不符合题意;
故选ABD.
【点睛】本题考查了平行线的性质与判定,属于简单题,熟悉平行线的判定方法和性质是解题关键.
12.AC
【分析】根据平行线间的距离、三角形的周长、面积以及角的定义逐项排查即可.
【详解】解:A.∵直线mn,∴点P到直线n的距离不变,,即A符合题意;
B.∵PA、PB的长度随点P的移动而变化,∴△PAB的周长会随点P的移动而变化,即B不符合题意;
C.∵点P到直线n的距离不变, AB的大小,∴△PAB的面积不变,即C符合题意;
D.∵直线m、n之间的距离不随点P的移动而变化,∴∠APB的大小随点P的移动而变化,即D不符合题意.
故选:AC.
【点睛】本题考查了点到直线的距离、等底等高的三角形的面积相等、平行线间的距离的定义等知识点,熟记相关定义和性质是解答本题的关键.
13.37°
【分析】如图,行平行线性质得出∠3=∠1=37°,再根据对顶角相等求解.
【详解】解:如图,
∵ab,
∴∠3=∠1=37°,
∵∠2=∠3,
∴∠2=37°,
故答案为:37°.
【点睛】本题考查平行线的性质,对顶角性质,熟练掌握平行线的性质是解题的关键.
14.40
【分析】根据四边形ABCD为长方形得AD∥BC,再根据平行线的性质得∠AEF+∠3=180°,则可计算出∠3=70°,然后根据折叠的性质得到∠2=∠3=70°,再利用平角的定义可计算出∠1.
【详解】如图,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEF+∠3=180°,
∴∠3=180°-110°=70°,
∵矩形ABCD沿EF对折后使两部分叠合,
∴∠2=∠3=70°,
∴∠1=180°-∠2-∠3=40°.
故答案为40.
【点睛】本题考查了平行线的性质以及折叠的性质.解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.
15.20
【分析】根据对顶角相等求出∠AMF,再求出∠AMN,然后根据两直线平行,内错角相等求解即可.
【详解】解:∵∠BME=110°,
∴ ∠AMF=∠BME=110°,
∵ MN⊥EF于M,
∴ ∠NMF=90°,
∴∠AMN=∠AMF-∠NMF=110°-90°=20°,
∵ABCD,
∴∠MND=∠AMN=20°.
故答案为:20.
【点睛】本题考查了平行线的性质,对顶角相等的性质,以及垂直的定义,是基础题,熟记性质并准确识图是解题的关键.
16.
【分析】根据两直线平行,内错角相等可得,,然后相加即可得解.
【详解】解:∵,,
∴,
∵,,
∴,
∴.
故答案为:.
【点睛】本题主要考查了平行线的性质,解决问题的关键是掌握:两直线平行,内错角相等.
17.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据平行线的定义作图即可;
(2)根据垂线段的定义作图即可;
(3)连接、即可.
【详解】(1)解:如图所示,如图所示,直线即为所求;
(2)如图所示,垂线段即为所求;
(3)如图所示,线段、即为所求.
【点睛】本题主要考查作图一复杂作图.解题的关键是熟练掌握平行线的定义、垂线段的定义.
18.另一侧以60°的角度铺设,理由见解析
【分析】根据两直线平行,同旁内角互补定理,已知角为120°,那么它的补角即可求出.
【详解】根据“同旁内角互补,两直线平行”,为了使管道对接,另一侧应以的角度铺设.
【点睛】本题主要考查了平行线的性质之一:两直线平行,同旁内角互补,熟练掌握平行线的性质是解答此题的关键.
19.∠C=100°.
【分析】先根据两直线平行求出∠CBE=100°,再利用角度转化即可计算.
【详解】
∵AD∥BC,∠A=100°,
∴∠CBE=∠A=100°,
∵∠1=∠2,∠1+∠C+∠COD=180°,∠CBE+∠2+∠BOE=180°,∠COD=∠BOE,
∴∠C=∠CBE=100°.
【点睛】本题考查角度转换,能够利用好两直线平行的条件是解题关键.
20.(1),理由见解析
(2)
【分析】(1)根据同角的补角相等得出,再根据内错角相等两直线平行即可得证;
(2)根据平行线的性质及等量代换得出,再根据同位角相等两直线平行得出,最后根据两直线平行同旁内角互补即可得出答案.
【详解】(1)解:,理由如下:
(2)由(1)知,
.
【点睛】本题考查了平行线的判定及性质,熟练掌握平行线的性质定理是解题的关键.
21.;;;对顶角相等;两直线平行,同旁内角互补;
【分析】根据角平分线的定义,即可得到∠ACM的度数,进而得出∠OCB的度数,再依据平行线的性质,即可得到∠O的度数.
【详解】解:∵平分,
∴.
∵∵,
∴.
∵直线与交于点C,,
∴(对顶角相等),
∵,
∴(两直线平行,同旁内角互补),
∴.
故答案为:;;;对顶角相等;两直线平行,同旁内角互补;.
【点晴】本题主要考查了角的计算,平行线的性质以及角平分线的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同旁内角互补.
22.(1)50°,140°
(2)∠ACB+∠DCE=180°,证明见解析
(3)①45°;②30°
【分析】对于(1),根据直角定义求出∠ACE的度数,即可求出∠ACB的度数;
对于(2),将∠ACB+∠DCE转化为∠ACE+∠BCE+∠DCE,再求出答案;
对于(3)①,先根据两直线平行内错角相等得出答案;
对于②,先根据两直线平行,同旁内角互补,求出∠ACB的度数,进而得出答案.
【详解】(1)∵∠ACD=90°,∠DCE=40°,
∴∠ACE=50°.
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=50°+90°=140°.
故答案为:50°,140°;
(2)∠ACB+∠DCE=180°.
理由如下:∠ACB+∠DCE=∠ACE+∠BCE+∠DCE=∠BCE+∠ACD=180°;
(3)①∵,
∴∠ACE=∠E=45°.
故答案为:45°;
②∵,
∴∠A+∠ACB=180°.
∵∠A=60°,
∴∠ACB=120°.
∵∠BCE=90°,
∴∠ACE=∠ACB-∠BCE==120°-90°=30°.
故答案为:30°.
【点睛】本题主要考查了角的和差,平行线的性质等,灵活选择平行线的性质是解题的关键.
23.(1)∠AEP+∠PFC=∠EPF;(2)∠AEP+∠EPF+∠PFC=360°;(3)①150°或30;②∠EPF+2∠EQF=360°或∠EPF=2∠EQF
【分析】(1)由于点是平行线,之间有一动点,因此需要对点的位置进行分类讨论:如图1,当点在的左侧时,,,满足数量关系为:;
(2)当点在的右侧时,,,满足数量关系为:;
(3)①若当点在的左侧时,;当点在的右侧时,可求得;
②结合①可得,由,得出;可得,由,得出.
【详解】解:(1)如图1,过点作,
,
,
,
,
,
;
(2)如图2,当点在的右侧时,,,满足数量关系为:;
过点作,
,
,
,
,
,
;
(3)①如图3,若当点在的左侧时,
,
,
,分别平分和,
,,
;
如图4,当点在的右侧时,
,
,
;
故答案为:或30;
②由①可知:,
;
,
.
综合以上可得与的数量关系为:或.
【点睛】本题主要考查了平行线的性质,平行公理和及推论等知识点,作辅助线后能求出各个角的度数,是解此题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,和属于同位角的有( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
2.下列说法中,正确的是( )
A.平面内,没有公共点的两条线段平行
B.平面内,没有公共点的两条射线平行
C.没有公共点的两条直线互相平行
D.互相平行的两条直线没有公共点
3.如图,下列能判定∥的条件有几个( )
(1) (2)(3) (4).
A.4 B.3 C.2 D.1
4.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
5.如图,将一副三角板按如图所示的方式摆放,其中两条斜边,角的顶点与含角的直角三角板的直角顶点重合,点,,在同一条直线上,则的为( )
A. B. C. D.
6.如图,,平分交于点E,若,则 ( )
A. B. C. D.
7.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的度数是( )
A. B. C. D.
8.如图, ,,,则( )
A. B. C. D.
二、多选题
9.如图所示,下列说法中正确的是( )
A.与是同旁内角; B.与是内错角;
C.与是内错角; D.与是同位角.
10.下列说法正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
11.如图,如果,,则下列结论正确的为( )
A. B. C.平分 D.
12.如图,点P在直线m上移动,A,B是直线n上的两个定点,且直线.对于下列各值,不会随点P的移动而变化的是( )
A.点P到直线n的距离 B.的周长
C.的面积 D.的大小
三、填空题
13.如图,,,则∠2等于______.
14.如图所示,把长方形ABCD沿EF对折,若∠AEF=110°,则∠1=_____°.
15.如图所示,ABCD,EF交AB于点M,MN⊥EF于点M,MN交CD于点N,若∠BME=110°,则∠MND的度数为_____度;
16.生活中常见的探照灯、汽车大灯等灯具都是凹面镜.如图,从光源P点照射到凹面镜上的光线等反射以后沿着与直线平行的方向射出,若,则的度数为________.
四、解答题
17.如图,直线与直线交于点,点为直线、外一点,根据下列语句画图,并作答:
(1)过点画交于点;
(2)过点画,垂足为;
(3)点为直线上一点,连接,连接.
18.如图,一条公路的两侧铺设了两条平行管道,如果公路一侧铺设的管道与纵向联通管道的角度为,那么,为了使管道对接,另一侧应以什么角度铺设纵向联通管道?为什么?
19.已知,如图,点A、B、E共线,AD∥BC,∠1=∠2,∠A=100°,求∠C的度数.
20.如图,已知
(1)判断AB与EF的位置关系,并说明理由;
(2)若,,求的度数.
21.如图,点C在的一边上,过点C的直线,平分.当时,求的度数.
解:∵平分,
∴= .
∵,
∴= °.
∵直线与交于点C,
∴== °( ),
∵,
∴( ),
∴= °.
22.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中∠A=60°,∠B=45°.
(1)如图1,若∠DCE=40°,则∠ACE= .∠ACB= .
(2)由(1)猜想∠ACB和∠DCE的数量关系,并证明你的结论:
(3)若固定△ACD,将△BCE绕点C旋转.
①如图2,当旋转至BEAC时,则∠ACE= .
②如图3,当旋转至BCAD时,则∠ACE= .
23.已知,定点,分别在直线,上,在平行线,之间有一动点.
(1)如图1所示时,试问,,满足怎样的数量关系 并说明理由.
(2)除了(1)的结论外,试问,,还可能满足怎样的数量关系 请画图并证明
(3)当满足,且,分别平分和,
①若,则__________°.
②猜想与的数量关系.(直接写出结论)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】同位角的定义是两条直线被第三条直线所截时,在截线的同旁,被截两条直线的同一侧的角,简单记忆为F形的两个角,很明显选①②⑤.
【详解】依据同位角的定义可以看出③的两个角并不是由3条线截取得到的,④中的而两个角不在截线的同旁,所以都不能选,①②⑤都符合条件.
【点睛】本题考查同位角的定义,能够熟记模型并运用模型进行判断是解题关键.
2.D
【分析】回忆线段之间、射线之间与直线之间的位置关系;对于A,可在纸上画出两条没有公共点的线段,观察两条线段的位置关系;对于B,可在纸上画出两条没有公共点的射线,观察两条线段的位置关系;对于C,思考若两条直线不在一个平面内,是否能够得到两条直线不平行也不相交,对于D,根据平行线的定义可作出判断.
【详解】对于A,如图所示,A错误;
对于B,如图所示,B错误;
对于C,如果两条直线不在同一个平面内,不相交也可能不平行,则C错误;
对于D,根据平行线的定义可知D正确.
故答案为D.
【点睛】本题考查了两条直线的位置关系,直线、射线、线段的定义,熟练掌握直线的位置关系及相关定义是本题解题的关键.
3.B
【分析】根据平行线的判定逐一判定即可.
【详解】因为,所有AD∥BC,故(1)错误.
因为,所以∥,故(2)正确.
因为,所以∥,故(3)正确.
因为,所以∥,故(4)正确.
所以共有3个正确条件.
故选B
【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.
4.C
【分析】根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.观察各个选项中角的数量关系(相等或互补)、位置关系是否符合上述三个定理,即可判断所给选项是否正确.
【详解】A. 因为和是同旁内角,所以根据不能得到,故A选项错误;
B. 因为和不是同位角也不是内错角,所以根据不能得到,故B选项错误;
C. 因为和是同旁内角,所以根据可以得到,故本选项正确;
D. 和虽然是同位角,但根据只可以得出,故本选项错误.
故本题选C.
【点睛】本题考查平行线的判定定理,在这里①判断两条直线是否平行,是根据角的数量关系(相等或互补)和位置关系去判定的,只有同时满足两种关系,才可根据定理判断平行;②完整的定理前面有一句两直线被第三条直线所截,找准截线和被截线很关键(例如D选项和是同位角,它们的被截线是AB和DE).
5.A
【分析】由题意得∠ADE=45°,∠BAC=30°,由平行线的性质得出∠BAD=∠ADE=45°,即可得出答案.
【详解】解:由题意得:∠ADE=45°,∠BAC=30°,
∵AB∥DE,
∴∠BAD=∠ADE=45°,
∴∠CAD=∠BAD-∠BAC=45°-30°=15°;
故选:A.
【点睛】本题考查了直角三角形的性质、平行线的性质等知识;熟练掌握平行线的性质是解题的关键.
6.A
【分析】如图:根据平角的定义及角平分线的性质求得的度数,再根据平行线的性质求解即可.
【详解】解:如图:
∵,
∴,
∵平分
∴,
∵,
∴,
∴.
故选:A.
【点睛】本题主要考查了平行线的性质、角平分线的定义等知识点,灵活运用平行线的性质是解答本题的关键.
7.B
【分析】根据平行线的性质即可求解.
【详解】解:延长BC至G,如下图所示,
由题意得,AF∥BE,AD∥BC,
∵AF∥BE,
∴∠1=∠3(两直线平行,同位角相等),
∵AD∥BC,
∴∠3=∠4(两直线平行,同位角相等),
∴∠4=∠1=40°,
∵CD∥BE,
∴∠6=∠4=40°(两直线平行,同位角相等),
∵这条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,
∴∠5=∠6=40°,
∴∠2=180°-∠5-∠6=180°-40°-40°=100°,
故选:B.
【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.
8.D
【分析】过点作,根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等得出,然后整理即可得解.
【详解】过点作,
(两直线平行,内错角相等),
,
(已知),
(平行于同一直线的两直线平行),
(两直线平行,同旁内角互补),
,
.
故选:D.
【点睛】本题考查了平行线的判定与性质,作辅助线构造出平行线是解题的关键.
9.ABD
【分析】根据同位角的定义:两条直线被第三条直线所截,在截线的同旁,被截两直线的同一侧的角叫做同位角;内错角的定义,两个角分别在截线的两侧,且在两条被截线之间,具有这样位置关系的一对角叫做内错角;同旁内角的定义:两条直线被第三条直线所截,在截线的同旁,且在被截的两条直线之内的两角,叫做同旁内角,进行逐一判断即可.
【详解】解:根据内错角、同旁内角和同位角的定义可知:A、B、D均是正确的符合题意,∠A与∠C是同旁内角,C不符合题意.
故选ABD.
【点睛】本题考查的知识点是同位角,内错角,同旁内角的概念,解题关键是熟记内错角、同旁内角和同位角的定义.
10.BCD
【分析】根据平行线的定义及平行公理进行判断.
【详解】A. 若点在直线上,则不可以作出已知直线的平行线,因此 “过任意一点可作已知直线的一条平行线”说法错误;
B. “同一平面内两条不相交的直线是平行线”说法正确;
C. “在同一平面内,过直线外一点只能画一条直线与已知直线垂直”说法正确;
D. “平行于同一直线的两直线平行”说法正确;
故选BCD.
【点睛】本题主要考查平行线的定义及平行公理,熟练掌握公理、定理是解决本题的关键.
11.ABD
【分析】根据平行线的性质和判定进行解题即可.
【详解】解:∵DE∥BC,
∴∠DCB=∠1,∠AED=∠ACB,故B符合题意;
∵∠1=∠2,
∴∠2=∠DCB,
∴FG∥DC,故A符合题意;
∴∠BFG=∠BDC,
又∵∠BDC+∠ADC=180°,
∴∠BFG+∠ADC=180°,故D符合题意;
∵∠BCD≠∠ACD,
∴CD平分∠ACB是错误的,故C不符合题意;
故选ABD.
【点睛】本题考查了平行线的性质与判定,属于简单题,熟悉平行线的判定方法和性质是解题关键.
12.AC
【分析】根据平行线间的距离、三角形的周长、面积以及角的定义逐项排查即可.
【详解】解:A.∵直线mn,∴点P到直线n的距离不变,,即A符合题意;
B.∵PA、PB的长度随点P的移动而变化,∴△PAB的周长会随点P的移动而变化,即B不符合题意;
C.∵点P到直线n的距离不变, AB的大小,∴△PAB的面积不变,即C符合题意;
D.∵直线m、n之间的距离不随点P的移动而变化,∴∠APB的大小随点P的移动而变化,即D不符合题意.
故选:AC.
【点睛】本题考查了点到直线的距离、等底等高的三角形的面积相等、平行线间的距离的定义等知识点,熟记相关定义和性质是解答本题的关键.
13.37°
【分析】如图,行平行线性质得出∠3=∠1=37°,再根据对顶角相等求解.
【详解】解:如图,
∵ab,
∴∠3=∠1=37°,
∵∠2=∠3,
∴∠2=37°,
故答案为:37°.
【点睛】本题考查平行线的性质,对顶角性质,熟练掌握平行线的性质是解题的关键.
14.40
【分析】根据四边形ABCD为长方形得AD∥BC,再根据平行线的性质得∠AEF+∠3=180°,则可计算出∠3=70°,然后根据折叠的性质得到∠2=∠3=70°,再利用平角的定义可计算出∠1.
【详解】如图,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠AEF+∠3=180°,
∴∠3=180°-110°=70°,
∵矩形ABCD沿EF对折后使两部分叠合,
∴∠2=∠3=70°,
∴∠1=180°-∠2-∠3=40°.
故答案为40.
【点睛】本题考查了平行线的性质以及折叠的性质.解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.
15.20
【分析】根据对顶角相等求出∠AMF,再求出∠AMN,然后根据两直线平行,内错角相等求解即可.
【详解】解:∵∠BME=110°,
∴ ∠AMF=∠BME=110°,
∵ MN⊥EF于M,
∴ ∠NMF=90°,
∴∠AMN=∠AMF-∠NMF=110°-90°=20°,
∵ABCD,
∴∠MND=∠AMN=20°.
故答案为:20.
【点睛】本题考查了平行线的性质,对顶角相等的性质,以及垂直的定义,是基础题,熟记性质并准确识图是解题的关键.
16.
【分析】根据两直线平行,内错角相等可得,,然后相加即可得解.
【详解】解:∵,,
∴,
∵,,
∴,
∴.
故答案为:.
【点睛】本题主要考查了平行线的性质,解决问题的关键是掌握:两直线平行,内错角相等.
17.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据平行线的定义作图即可;
(2)根据垂线段的定义作图即可;
(3)连接、即可.
【详解】(1)解:如图所示,如图所示,直线即为所求;
(2)如图所示,垂线段即为所求;
(3)如图所示,线段、即为所求.
【点睛】本题主要考查作图一复杂作图.解题的关键是熟练掌握平行线的定义、垂线段的定义.
18.另一侧以60°的角度铺设,理由见解析
【分析】根据两直线平行,同旁内角互补定理,已知角为120°,那么它的补角即可求出.
【详解】根据“同旁内角互补,两直线平行”,为了使管道对接,另一侧应以的角度铺设.
【点睛】本题主要考查了平行线的性质之一:两直线平行,同旁内角互补,熟练掌握平行线的性质是解答此题的关键.
19.∠C=100°.
【分析】先根据两直线平行求出∠CBE=100°,再利用角度转化即可计算.
【详解】
∵AD∥BC,∠A=100°,
∴∠CBE=∠A=100°,
∵∠1=∠2,∠1+∠C+∠COD=180°,∠CBE+∠2+∠BOE=180°,∠COD=∠BOE,
∴∠C=∠CBE=100°.
【点睛】本题考查角度转换,能够利用好两直线平行的条件是解题关键.
20.(1),理由见解析
(2)
【分析】(1)根据同角的补角相等得出,再根据内错角相等两直线平行即可得证;
(2)根据平行线的性质及等量代换得出,再根据同位角相等两直线平行得出,最后根据两直线平行同旁内角互补即可得出答案.
【详解】(1)解:,理由如下:
(2)由(1)知,
.
【点睛】本题考查了平行线的判定及性质,熟练掌握平行线的性质定理是解题的关键.
21.;;;对顶角相等;两直线平行,同旁内角互补;
【分析】根据角平分线的定义,即可得到∠ACM的度数,进而得出∠OCB的度数,再依据平行线的性质,即可得到∠O的度数.
【详解】解:∵平分,
∴.
∵∵,
∴.
∵直线与交于点C,,
∴(对顶角相等),
∵,
∴(两直线平行,同旁内角互补),
∴.
故答案为:;;;对顶角相等;两直线平行,同旁内角互补;.
【点晴】本题主要考查了角的计算,平行线的性质以及角平分线的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同旁内角互补.
22.(1)50°,140°
(2)∠ACB+∠DCE=180°,证明见解析
(3)①45°;②30°
【分析】对于(1),根据直角定义求出∠ACE的度数,即可求出∠ACB的度数;
对于(2),将∠ACB+∠DCE转化为∠ACE+∠BCE+∠DCE,再求出答案;
对于(3)①,先根据两直线平行内错角相等得出答案;
对于②,先根据两直线平行,同旁内角互补,求出∠ACB的度数,进而得出答案.
【详解】(1)∵∠ACD=90°,∠DCE=40°,
∴∠ACE=50°.
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=50°+90°=140°.
故答案为:50°,140°;
(2)∠ACB+∠DCE=180°.
理由如下:∠ACB+∠DCE=∠ACE+∠BCE+∠DCE=∠BCE+∠ACD=180°;
(3)①∵,
∴∠ACE=∠E=45°.
故答案为:45°;
②∵,
∴∠A+∠ACB=180°.
∵∠A=60°,
∴∠ACB=120°.
∵∠BCE=90°,
∴∠ACE=∠ACB-∠BCE==120°-90°=30°.
故答案为:30°.
【点睛】本题主要考查了角的和差,平行线的性质等,灵活选择平行线的性质是解题的关键.
23.(1)∠AEP+∠PFC=∠EPF;(2)∠AEP+∠EPF+∠PFC=360°;(3)①150°或30;②∠EPF+2∠EQF=360°或∠EPF=2∠EQF
【分析】(1)由于点是平行线,之间有一动点,因此需要对点的位置进行分类讨论:如图1,当点在的左侧时,,,满足数量关系为:;
(2)当点在的右侧时,,,满足数量关系为:;
(3)①若当点在的左侧时,;当点在的右侧时,可求得;
②结合①可得,由,得出;可得,由,得出.
【详解】解:(1)如图1,过点作,
,
,
,
,
,
;
(2)如图2,当点在的右侧时,,,满足数量关系为:;
过点作,
,
,
,
,
,
;
(3)①如图3,若当点在的左侧时,
,
,
,分别平分和,
,,
;
如图4,当点在的右侧时,
,
,
;
故答案为:或30;
②由①可知:,
;
,
.
综合以上可得与的数量关系为:或.
【点睛】本题主要考查了平行线的性质,平行公理和及推论等知识点,作辅助线后能求出各个角的度数,是解此题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
