青岛版数学七年级下册第9章 平行线 单元复习试题(含解析)
文档属性
| 名称 | 青岛版数学七年级下册第9章 平行线 单元复习试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 583.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 00:00:00 | ||
图片预览




文档简介
青岛版七年级下册第9章 平行线单元测试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行 C.平行或相交 D.平行或相交或重合
2.如图,在同一平面内过直线l外一点A作直线l的平行线,可作平行线的条数有( )
A.0条 B.1条 C.2条 D.无数条
3.下列图中,不是同位角的是( )
A. B. C. D.
4.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同旁内角互补
C.同位角相等,两直线平行 D.两直线平行,同位角相等
5.如图:AB∥CD,点E是CD上一点,∠AEC=36°,EF平分∠AED交AB于点F,则∠AFE的度数( )
A. B. C. D.
6.如图,直线a,b被直线c所截,下列条件中,不能得到的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3+∠4=180° D.∠1+∠4=180°
7.一把直尺和一块三角尺如图放置,,则的度数为( )
A. B. C. D.
8.如图,直线a,b,c被直线d所截,,若,则的度数为( )
A. B. C. D.
9.如图, ,,,则的度数为( )
A. B. C. D.
10.如图,,,,则的度数为( )
A. B. C. D.
11.如图, ,,,则( )
A. B. C. D.
12.一副三角板按如图放置,则下列结论:①如果∠2=30°,则有AC//DE;②如果BC//AD,则有∠2=45°;③∠BAE+∠CAD随着∠2的变化而变化;④如果∠4=45°,那么∠1=60°,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
13.如图,∠2的内错角是_______,∠3与∠B是_______,∠B的同旁内角是_______.
14.如图,CD平分,且,若∠A =36°,则_______.
15.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=___________°.
16.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=22°,则∠2的度数为______.
17.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A=___.
三、解答题
18.请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.
理由:∵∠A=∠F(已知)
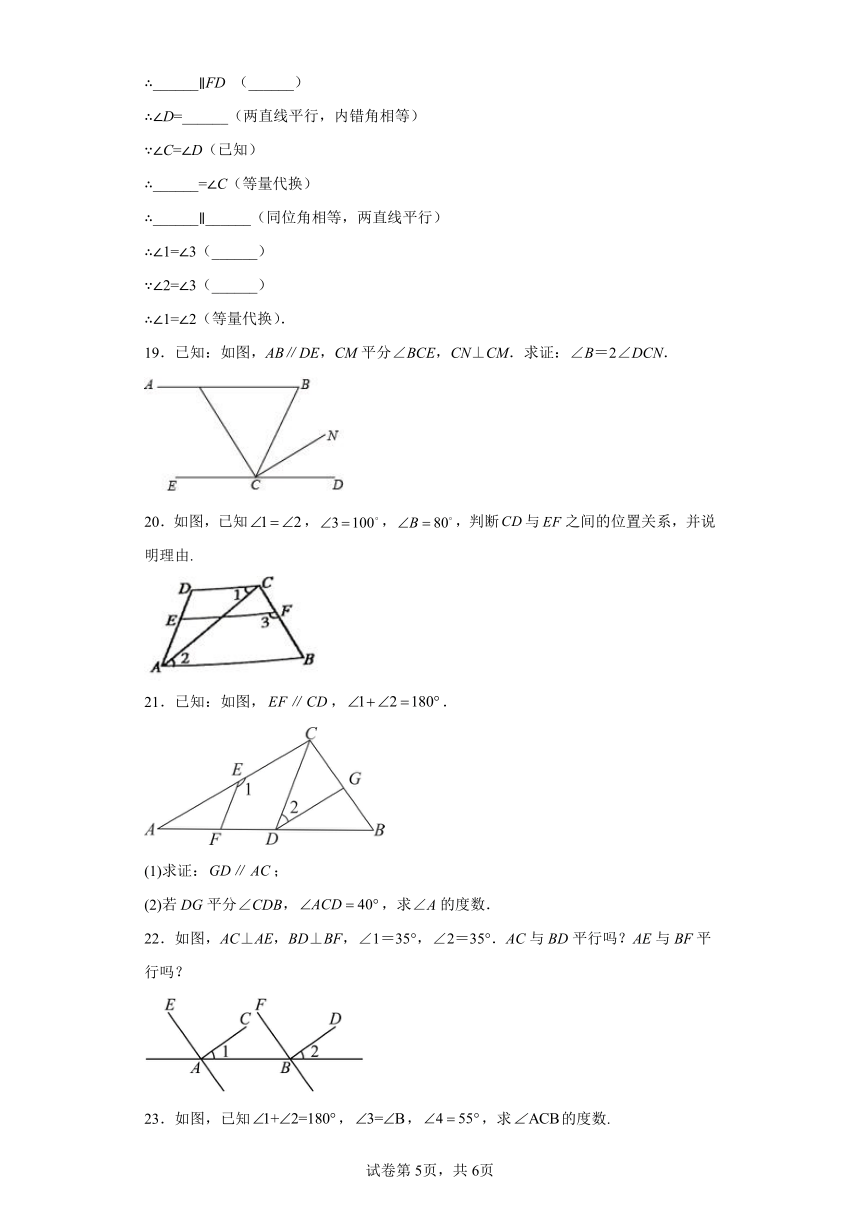
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
19.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
20.如图,已知,,,判断与之间的位置关系,并说明理由.
21.已知:如图,,.
(1)求证:;
(2)若DG平分∠CDB,,求∠A的度数.
22.如图,AC⊥AE,BD⊥BF,∠1=35°,∠2=35°.AC与BD平行吗?AE与BF平行吗?
23.如图,已知,,,求的度数.
24.如图,直线,相交于点,平分,平分,,垂足为,那么,请说明理由.
25.先阅读再解答:
(1)如图1,,试说明:;
(2)已知:如图2,,求证:;
(3)已知:如图3,,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】试题分析:利用同一个平面内,两条直线的位置关系解答.
解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选C.
考点:相交线;垂线;平行线.
2.B
【分析】根据平行线的基本性质,可以直接得结论.
【详解】解:根据平行线的基本性质,在同一平面内,经过直线外一点,有且只有一条直线与这条直线平行,
所以在同一平面内过直线l外一点A作直线l的平行线,可作平行线的条数有1条,
故答案为:B.
【点睛】本题考查平行线的基本性质,掌握经过直线外一点,有且只有一条直线与这条直线平行是解答本题的关键.
3.D
【分析】根据同位角的定义(在被截线同一侧,截线的同一方位的两个角互为同位角)解决此题.
【详解】解:A.由图可知,,是同位角,故不符合题意.
B.由图可知,,是同位角,故不符合题意.
C.由图可知,,是同位角,故不符合题意.
D.由图可知,,不是同位角,故符合题意.
故选:D.
【点睛】本题主要考查同位角,解题的关键是熟练掌握同位角的定义.
4.C
【分析】根据和是三角板中的同一个角,得,根据平行线的判定,即可.
【详解】∵,
∴(同位角相等,两直线平行),
∴C正确.
故选:C.
【点睛】本题考查平行线的判定,解题的关键是掌握平行线的判定.
5.C
【分析】由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
【详解】解:∵∠AEC=36°,
∴∠AED=180°-∠AEC=144°,
∵EF平分∠AED,
∴∠DEF= ∠AED=72°,
又∵AB∥CD,
∴∠AFE=∠DEF=72°.
故选C.
【点睛】本题考查的是平行线的性质以及角平分线的定义.熟练掌握平行线的性质,求出∠DEF的度数是解决问题的关键.
6.A
【分析】根据平行线的判定定理判断求解即可.
【详解】解:A.由∠1=∠3,不能判定a∥b,故选项符合题意;
B.∵∠2=∠4,
∴a∥b,
故选项不符合题意;
C.∵∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
D.∵∠1+∠4=180°,∠1=∠3,
∴∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
故选:A.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
7.A
【分析】设直尺的两边分别为,过点作,根据平行线的性质可得,,根据即可求得.
【详解】如图,设直尺的两边分别为,过点作,
故选A
【点睛】本题考查了平行线的性质与判定求角度,掌握平行线的性质是解题的关键.
8.A
【分析】先根据求出的度数,由对顶角相等求出的度数,根据即可得出结论.
【详解】解:如图,
∵,
∴,
∴,
∵,
∴.
故选:A.
【点睛】本题考查的是平行线的性质,熟知两直线平行,同位角相等;两直线平行,同旁内角互补是解题的关键.
9.B
【分析】根据平行线的性质即可求解.
【详解】如图,设交于点,
,,
故选:B.
【点睛】本题考查了平行线的性质,掌握平行线的性质是解题的关键.
10.C
【分析】根据两直线平行,同位角相等,得出,再根据两直线平行,同位角相等,即可得出的度数.
【详解】解:∵,
∴,
又∵,
∴.
故选:C
【点睛】本题考查了平行线的性质,解本题的关键在熟练掌握平行线的性质.
11.D
【分析】过点作,根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等得出,然后整理即可得解.
【详解】过点作,
(两直线平行,内错角相等),
,
(已知),
(平行于同一直线的两直线平行),
(两直线平行,同旁内角互补),
,
.
故选:D.
【点睛】本题考查了平行线的判定与性质,作辅助线构造出平行线是解题的关键.
12.B
【分析】根据平行线的判定与性质即可逐一进行证明.
【详解】解:①∵∠2=30°,
∴∠1=90°﹣∠2=60°,
∵∠AED=60°,
∴∠1=∠AED,
∴AC//DE;
所以①正确;
②∵BC//AE,
∴∠B=∠3=45°,
∴∠2=90°﹣∠3=45°;
所以②正确;
③∵∠1+∠2=∠3+∠2=90°,
∴∠BAE+∠CAD=∠1+∠2+∠2+∠3=180°,
∴∠BAE+∠CAD随着∠2的变化不会发生变化;
所以③错误;
④如图,
∵∠EGF=∠4=45°,∠FEG=60°,
∴∠GFA=45°+60°=105°,
∵∠GFA=∠C+∠1,∠C=45°,
∴∠1=60°.
所以④正确.
所以其中正确的是①②④.
故选:B.
【点睛】本题考查平行线的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.
13. ∠C; 内错; ∠1或∠DAB或∠C
【详解】解:∠2和∠C在截线AD和BC的内部,被截线AC的两侧,故∠2的内错角是∠C,
∠3与∠B在截线AE和BC的内部,被截线AB的两侧,故∠3与∠B是内错角,
∠B的同旁内角是∠1或∠DAB或∠C.
故答案为:∠C;内错;∠1或∠DAB或∠C.
14.36°
【分析】先根据平行线的性质,得出∠A=∠ECD,∠B=∠BCD,再根据角平分线的定义,即可得到∠ECD=∠BCD,进而得出∠B=∠A =36°.
【详解】解:∵,
∴∠A=∠ECD,∠B=∠BCD,
∵CD平分,
∴∠ECD=∠BCD,
∴∠B=∠A =36°.
故答案为36°.
15.40
【详解】
∵PM⊥l
∴∠2+∠3=90°
∵a∥b
∴∠1=∠3=50°
∴∠2=40°
故答案为:40
16.52°
【分析】根据平行线的性质即可得到结论.
【详解】解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+22°=52°,
故答案为:52°
【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
17.110 /110度
【分析】根据平行线的性质和角平分线的性质可得结论.
【详解】解:∵AD//BC
∴
∵CE平分∠DCF
∴
∴
∵AB//CD
∴
∵AD//BC
∴
∴
故答案为:110
【点睛】本题主要考查了角的平分线以及平行线的性质,熟练掌握平行线的性质是解答本题的关键.
18.AC 内错角相等,两直线平行 ∠DBA ∠DBA CE BD 两直线平行,同位角相等 对顶角相等
【分析】欲证明∠1=∠2,只需推知∠1=∠3=∠2.
【详解】证明:∵∠A=∠F(已知)
∴AC∥FD ( 内错角相等,两直线平行)
∴∠D=∠DBA(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴∠DBA=∠C(等量代换)
∴CE∥BD(同位角相等,两直线平行)
∴∠1=∠3( 两直线平行,同位角相等)
∵∠2=∠3( 对顶角相等)
∴∠1=∠2(等量代换).
故答案是:AC;内错角相等,两直线平行;∠DBA;∠DBA;CE;BD;两直线平行,同位角相等; 对顶角相等.
【点睛】本题主要考查了平行线的性质与判定的综合应用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
19.见解析
【分析】先根据平行线的性质得出∠B+∠BCE=180°,∠B=∠BCD,再根据CM平分∠BCE可知∠1=∠2,再由CN⊥CM可知,∠2+∠3=90°,故∠1+∠4=90°,所以∠3=∠4,故可得出结论.
【详解】证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
20.,见解析.
【分析】由可得,由∠3、∠B的关系可判断AB与EF的关系,进一步即可解答.
【详解】解:,理由如下:
因为,
所以,
又因为,,
所以,
所以,
所以.
【点睛】本题考查了平行线的判定和平行公理的推论,熟练掌握平行线的判定方法是解题的关键.
21.(1)证明见解析
(2)
【分析】(1)先证明,结合,可得,从而可得结论;
(2)先证明,再证明,再利用平行线的性质证明即可.
【详解】(1)证明:∵,
∴,
又∵,
∴,
∴;
(2)∵,
∴,
∵DG平分∠CDB,
∴,
∵,
∴.
【点睛】本题考查的是平行线的判定与性质,角平分线的定义,熟练的利用平行线的性质得到角与角之间的关系是解本题的关键.
22.平行,,平行,理由见解析
【分析】根据平行线的判定可得出,再根据已知条件可得出,即可得出.
【详解】解:,,理由如下:
,
(同位角相等,两直线平行),
又,
,
,
(同位角相等,两直线平行).
【点睛】本题考查了平行线的判定,解题的关键是掌握平行线的判定的方法.
23.55°
【分析】由已知条件和邻补角得出∠1=∠AEC,证出AB∥DF,得出内错角相等∠AEF=∠3,由已知条件得出∠AEF=∠B,证出EF∥BC,得出同位角相等即可.
【详解】解:∵∠1+∠2=180°,∠AEC+∠2=180°,
∴∠1=∠AEC,
∴AB∥DF,
∴∠AEF=∠3,
∵∠3=∠B,
∴∠AEF=∠B,
∴EF∥BC,
∴∠ACB=∠4=55°.
【点睛】本题考查了平行线的判定与性质、邻补角关系;熟练掌握平行线的判定和性质,证明EF∥BC是解决问题的关键
24.见解析
【分析】根据角平分线的定义得到,,根据垂直的定义得到,根据平行线的判定定理即可得到结论.
【详解】证明:∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查了角平分线的定义,平行线的判定,熟练掌握平行线的判定是解题的关键.
25.(1)证明见解析
(2)证明见解析
(3)证明见解析
【分析】(1)过点E作,由平行线的性质可得,进而可求解;
(2)过点E作,由平行线的性质可得,进而可求解;
(3)延长和反向延长相交于点G,由平行线的性质可得,进而可得,利用平行线的判定条件可证明,再根据平行线性质可证明结论.
【详解】(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查平行线的判定和性质,灵活运用平行线的性质证明是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在同一平面内两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行 C.平行或相交 D.平行或相交或重合
2.如图,在同一平面内过直线l外一点A作直线l的平行线,可作平行线的条数有( )
A.0条 B.1条 C.2条 D.无数条
3.下列图中,不是同位角的是( )
A. B. C. D.
4.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同旁内角互补
C.同位角相等,两直线平行 D.两直线平行,同位角相等
5.如图:AB∥CD,点E是CD上一点,∠AEC=36°,EF平分∠AED交AB于点F,则∠AFE的度数( )
A. B. C. D.
6.如图,直线a,b被直线c所截,下列条件中,不能得到的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3+∠4=180° D.∠1+∠4=180°
7.一把直尺和一块三角尺如图放置,,则的度数为( )
A. B. C. D.
8.如图,直线a,b,c被直线d所截,,若,则的度数为( )
A. B. C. D.
9.如图, ,,,则的度数为( )
A. B. C. D.
10.如图,,,,则的度数为( )
A. B. C. D.
11.如图, ,,,则( )
A. B. C. D.
12.一副三角板按如图放置,则下列结论:①如果∠2=30°,则有AC//DE;②如果BC//AD,则有∠2=45°;③∠BAE+∠CAD随着∠2的变化而变化;④如果∠4=45°,那么∠1=60°,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
13.如图,∠2的内错角是_______,∠3与∠B是_______,∠B的同旁内角是_______.
14.如图,CD平分,且,若∠A =36°,则_______.
15.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=___________°.
16.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=22°,则∠2的度数为______.
17.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A=___.
三、解答题
18.请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.
理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
19.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
20.如图,已知,,,判断与之间的位置关系,并说明理由.
21.已知:如图,,.
(1)求证:;
(2)若DG平分∠CDB,,求∠A的度数.
22.如图,AC⊥AE,BD⊥BF,∠1=35°,∠2=35°.AC与BD平行吗?AE与BF平行吗?
23.如图,已知,,,求的度数.
24.如图,直线,相交于点,平分,平分,,垂足为,那么,请说明理由.
25.先阅读再解答:
(1)如图1,,试说明:;
(2)已知:如图2,,求证:;
(3)已知:如图3,,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】试题分析:利用同一个平面内,两条直线的位置关系解答.
解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选C.
考点:相交线;垂线;平行线.
2.B
【分析】根据平行线的基本性质,可以直接得结论.
【详解】解:根据平行线的基本性质,在同一平面内,经过直线外一点,有且只有一条直线与这条直线平行,
所以在同一平面内过直线l外一点A作直线l的平行线,可作平行线的条数有1条,
故答案为:B.
【点睛】本题考查平行线的基本性质,掌握经过直线外一点,有且只有一条直线与这条直线平行是解答本题的关键.
3.D
【分析】根据同位角的定义(在被截线同一侧,截线的同一方位的两个角互为同位角)解决此题.
【详解】解:A.由图可知,,是同位角,故不符合题意.
B.由图可知,,是同位角,故不符合题意.
C.由图可知,,是同位角,故不符合题意.
D.由图可知,,不是同位角,故符合题意.
故选:D.
【点睛】本题主要考查同位角,解题的关键是熟练掌握同位角的定义.
4.C
【分析】根据和是三角板中的同一个角,得,根据平行线的判定,即可.
【详解】∵,
∴(同位角相等,两直线平行),
∴C正确.
故选:C.
【点睛】本题考查平行线的判定,解题的关键是掌握平行线的判定.
5.C
【分析】由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
【详解】解:∵∠AEC=36°,
∴∠AED=180°-∠AEC=144°,
∵EF平分∠AED,
∴∠DEF= ∠AED=72°,
又∵AB∥CD,
∴∠AFE=∠DEF=72°.
故选C.
【点睛】本题考查的是平行线的性质以及角平分线的定义.熟练掌握平行线的性质,求出∠DEF的度数是解决问题的关键.
6.A
【分析】根据平行线的判定定理判断求解即可.
【详解】解:A.由∠1=∠3,不能判定a∥b,故选项符合题意;
B.∵∠2=∠4,
∴a∥b,
故选项不符合题意;
C.∵∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
D.∵∠1+∠4=180°,∠1=∠3,
∴∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
故选:A.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
7.A
【分析】设直尺的两边分别为,过点作,根据平行线的性质可得,,根据即可求得.
【详解】如图,设直尺的两边分别为,过点作,
故选A
【点睛】本题考查了平行线的性质与判定求角度,掌握平行线的性质是解题的关键.
8.A
【分析】先根据求出的度数,由对顶角相等求出的度数,根据即可得出结论.
【详解】解:如图,
∵,
∴,
∴,
∵,
∴.
故选:A.
【点睛】本题考查的是平行线的性质,熟知两直线平行,同位角相等;两直线平行,同旁内角互补是解题的关键.
9.B
【分析】根据平行线的性质即可求解.
【详解】如图,设交于点,
,,
故选:B.
【点睛】本题考查了平行线的性质,掌握平行线的性质是解题的关键.
10.C
【分析】根据两直线平行,同位角相等,得出,再根据两直线平行,同位角相等,即可得出的度数.
【详解】解:∵,
∴,
又∵,
∴.
故选:C
【点睛】本题考查了平行线的性质,解本题的关键在熟练掌握平行线的性质.
11.D
【分析】过点作,根据两直线平行,同旁内角互补可得,再根据两直线平行,内错角相等得出,然后整理即可得解.
【详解】过点作,
(两直线平行,内错角相等),
,
(已知),
(平行于同一直线的两直线平行),
(两直线平行,同旁内角互补),
,
.
故选:D.
【点睛】本题考查了平行线的判定与性质,作辅助线构造出平行线是解题的关键.
12.B
【分析】根据平行线的判定与性质即可逐一进行证明.
【详解】解:①∵∠2=30°,
∴∠1=90°﹣∠2=60°,
∵∠AED=60°,
∴∠1=∠AED,
∴AC//DE;
所以①正确;
②∵BC//AE,
∴∠B=∠3=45°,
∴∠2=90°﹣∠3=45°;
所以②正确;
③∵∠1+∠2=∠3+∠2=90°,
∴∠BAE+∠CAD=∠1+∠2+∠2+∠3=180°,
∴∠BAE+∠CAD随着∠2的变化不会发生变化;
所以③错误;
④如图,
∵∠EGF=∠4=45°,∠FEG=60°,
∴∠GFA=45°+60°=105°,
∵∠GFA=∠C+∠1,∠C=45°,
∴∠1=60°.
所以④正确.
所以其中正确的是①②④.
故选:B.
【点睛】本题考查平行线的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.
13. ∠C; 内错; ∠1或∠DAB或∠C
【详解】解:∠2和∠C在截线AD和BC的内部,被截线AC的两侧,故∠2的内错角是∠C,
∠3与∠B在截线AE和BC的内部,被截线AB的两侧,故∠3与∠B是内错角,
∠B的同旁内角是∠1或∠DAB或∠C.
故答案为:∠C;内错;∠1或∠DAB或∠C.
14.36°
【分析】先根据平行线的性质,得出∠A=∠ECD,∠B=∠BCD,再根据角平分线的定义,即可得到∠ECD=∠BCD,进而得出∠B=∠A =36°.
【详解】解:∵,
∴∠A=∠ECD,∠B=∠BCD,
∵CD平分,
∴∠ECD=∠BCD,
∴∠B=∠A =36°.
故答案为36°.
15.40
【详解】
∵PM⊥l
∴∠2+∠3=90°
∵a∥b
∴∠1=∠3=50°
∴∠2=40°
故答案为:40
16.52°
【分析】根据平行线的性质即可得到结论.
【详解】解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+22°=52°,
故答案为:52°
【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
17.110 /110度
【分析】根据平行线的性质和角平分线的性质可得结论.
【详解】解:∵AD//BC
∴
∵CE平分∠DCF
∴
∴
∵AB//CD
∴
∵AD//BC
∴
∴
故答案为:110
【点睛】本题主要考查了角的平分线以及平行线的性质,熟练掌握平行线的性质是解答本题的关键.
18.AC 内错角相等,两直线平行 ∠DBA ∠DBA CE BD 两直线平行,同位角相等 对顶角相等
【分析】欲证明∠1=∠2,只需推知∠1=∠3=∠2.
【详解】证明:∵∠A=∠F(已知)
∴AC∥FD ( 内错角相等,两直线平行)
∴∠D=∠DBA(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴∠DBA=∠C(等量代换)
∴CE∥BD(同位角相等,两直线平行)
∴∠1=∠3( 两直线平行,同位角相等)
∵∠2=∠3( 对顶角相等)
∴∠1=∠2(等量代换).
故答案是:AC;内错角相等,两直线平行;∠DBA;∠DBA;CE;BD;两直线平行,同位角相等; 对顶角相等.
【点睛】本题主要考查了平行线的性质与判定的综合应用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
19.见解析
【分析】先根据平行线的性质得出∠B+∠BCE=180°,∠B=∠BCD,再根据CM平分∠BCE可知∠1=∠2,再由CN⊥CM可知,∠2+∠3=90°,故∠1+∠4=90°,所以∠3=∠4,故可得出结论.
【详解】证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
20.,见解析.
【分析】由可得,由∠3、∠B的关系可判断AB与EF的关系,进一步即可解答.
【详解】解:,理由如下:
因为,
所以,
又因为,,
所以,
所以,
所以.
【点睛】本题考查了平行线的判定和平行公理的推论,熟练掌握平行线的判定方法是解题的关键.
21.(1)证明见解析
(2)
【分析】(1)先证明,结合,可得,从而可得结论;
(2)先证明,再证明,再利用平行线的性质证明即可.
【详解】(1)证明:∵,
∴,
又∵,
∴,
∴;
(2)∵,
∴,
∵DG平分∠CDB,
∴,
∵,
∴.
【点睛】本题考查的是平行线的判定与性质,角平分线的定义,熟练的利用平行线的性质得到角与角之间的关系是解本题的关键.
22.平行,,平行,理由见解析
【分析】根据平行线的判定可得出,再根据已知条件可得出,即可得出.
【详解】解:,,理由如下:
,
(同位角相等,两直线平行),
又,
,
,
(同位角相等,两直线平行).
【点睛】本题考查了平行线的判定,解题的关键是掌握平行线的判定的方法.
23.55°
【分析】由已知条件和邻补角得出∠1=∠AEC,证出AB∥DF,得出内错角相等∠AEF=∠3,由已知条件得出∠AEF=∠B,证出EF∥BC,得出同位角相等即可.
【详解】解:∵∠1+∠2=180°,∠AEC+∠2=180°,
∴∠1=∠AEC,
∴AB∥DF,
∴∠AEF=∠3,
∵∠3=∠B,
∴∠AEF=∠B,
∴EF∥BC,
∴∠ACB=∠4=55°.
【点睛】本题考查了平行线的判定与性质、邻补角关系;熟练掌握平行线的判定和性质,证明EF∥BC是解决问题的关键
24.见解析
【分析】根据角平分线的定义得到,,根据垂直的定义得到,根据平行线的判定定理即可得到结论.
【详解】证明:∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查了角平分线的定义,平行线的判定,熟练掌握平行线的判定是解题的关键.
25.(1)证明见解析
(2)证明见解析
(3)证明见解析
【分析】(1)过点E作,由平行线的性质可得,进而可求解;
(2)过点E作,由平行线的性质可得,进而可求解;
(3)延长和反向延长相交于点G,由平行线的性质可得,进而可得,利用平行线的判定条件可证明,再根据平行线性质可证明结论.
【详解】(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查平行线的判定和性质,灵活运用平行线的性质证明是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
