等腰三角形（2）[下学期]

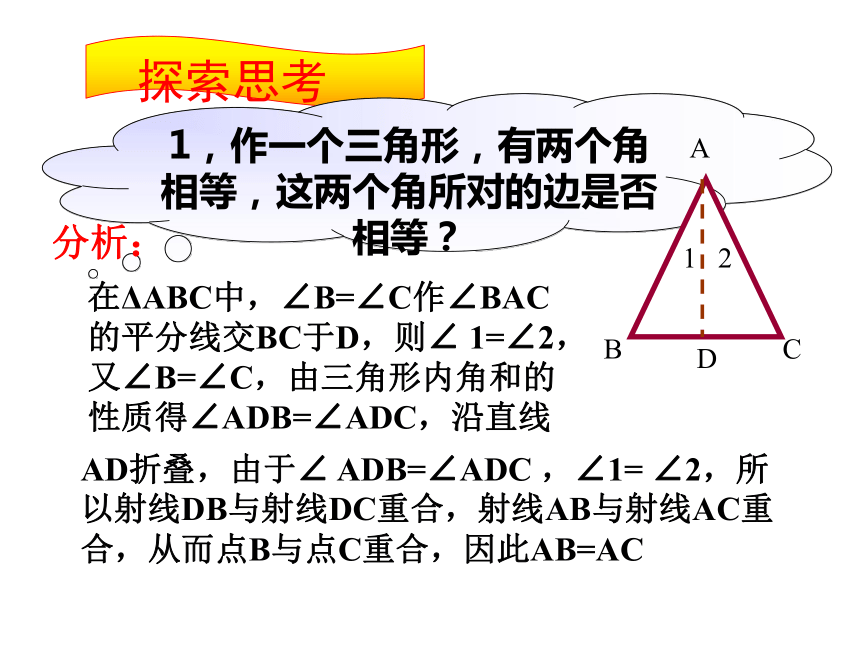
课件8张PPT。等腰三角形(二)1、什么样的图形叫等腰三角形？2 、等腰三角形有什么性质？ABC有两边相等的三角形是等腰三角形1）、等腰三角形的顶角平分线也是底边上的中线和底边上的高。2）、等腰三角形是轴对称图形。3）、等腰三角形的两底角相等。（等边对等角）1，作一个三角形，有两个角相等，这两个角所对的边是否相等？ABC在ΔABC中，∠B=∠C作∠BAC的平分线交BC于D，则∠ 1=∠2，又∠B=∠C，由三角形内角和的性质得∠ADB=∠ADC，沿直线分析：AD折叠，由于∠ ADB=∠ADC ，∠1= ∠2，所以射线DB与射线DC重合，射线AB与射线AC重合，从而点B与点C重合，因此AB=ACD12有两个角相等的三角形是等腰三角形简称“等角对等边”注意：（1）“等边对等角”与“等角对等边”，前者是等腰三角形的性质，后者是等腰三角形的判定。（2）“等边对等角”与“等角对等边”只是针对同一个三角形中的边角关系的。例：如果三角形一个角的外的角平分线平行于三角形的第三边，那么这个三角形是等腰三角形吗？为什么？ABCD12解：∠CAB是ΔABC的外角，∠1=∠2，AD∥BC，因为AD∥BC所以∠1=∠B
∠2=∠C，∠B=∠C，因此AB=AC，即ΔABC的是等腰例2：上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°， ∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解：∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC（等角对等边）
∵AB=20（12-10）=40
∴BC=40
答：B处到达灯塔C40海里ABCDE求证：等腰三角形的顶角顶点到两底角的角平分线的距离相等已知ΔABC中AB=AC，CE，BD是∠B， ∠C的平分线且AD⊥BD，AE⊥ECD求证：AD=AEO课堂小结：本课时有什么收获？学习了等到腰三角形的判定方法，“等角对等边”课堂 小测；能力 测试P54基础练习作业：P198练习：P195B组，1