青岛版数学五年级上册 六、团体操表演——因数与倍数-我学会了吗?课件(共26张PPT)
文档属性
| 名称 | 青岛版数学五年级上册 六、团体操表演——因数与倍数-我学会了吗?课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
我学会了吗?
复习方法
复习内容
将整理的知识与同伴进行交流,相互补充,并展示整理结果。
回忆本单元所学知识,尝试归纳、整理,用自己喜欢的形式表示出来。
1
2
4
基础练习
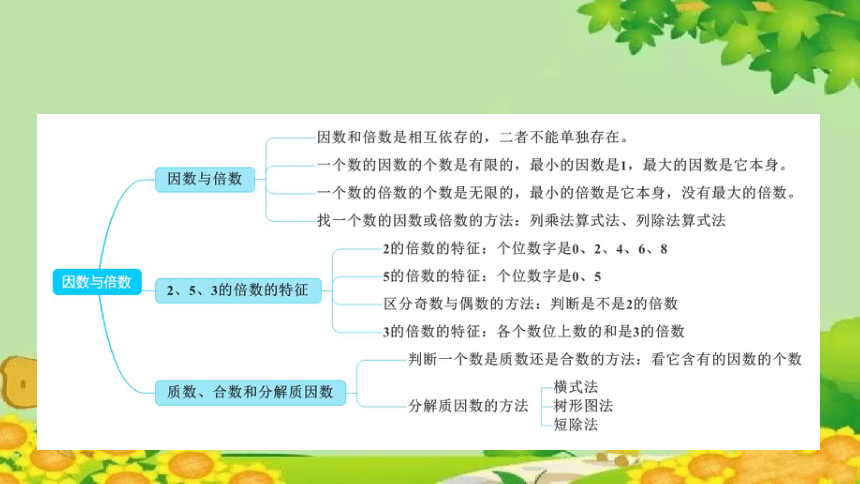
找一个数的因数或倍数
分解质因数的方法
2、5、3的倍数的特征
3
质数和合数的意义
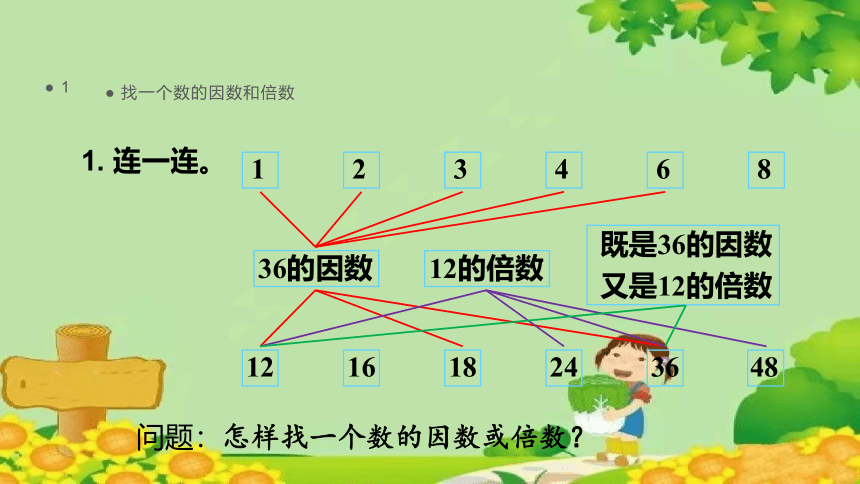
1. 连一连。
问题:怎样找一个数的因数或倍数?
找一个数的因数和倍数
1
48
2
3
4
6
8
12
16
18
24
36
36的因数
12的倍数
既是36的因数
又是12的倍数
1
(1)因为0.8×4=3.2,所以3.2是0.8的倍数。( )
(2)一个数的倍数一定比它的因数大。 ( )
(3)在48÷4=12中,48是12的倍数。 ( )
(4)1是所有非0自然数的因数。 ( )
2. 判断。(对的画“√”,错的画“×”)
问题:哪一句话是错误的,为什么?你能改正过来吗?
1
×
×
√
√
整数除法
不一定
找一个数的因数和倍数
2
3.从下列四张卡片中任选三张,按要求组成三位数。
2、5、3的倍数的特征
3
0
6
5
3的倍数:_____________________________________________
5的倍数: _____________________________________________
同时是2和3的倍数: ____________________________________
306、360、603、630
360、630、305、350、530、365、635、650、560、605
306、360、630
2
3.从下列四张卡片中任选三张,按要求组成三位数。
2、5、3的倍数的特征
3
0
6
5
问题:2、5、3的倍数的特征分别是什么?
同时是2和5的倍数: ____________________________________
同时是3和5的倍数: ____________________________________
同时是2、3和5的倍数: _________________________________
360、630、350、530、650、560
360、630
360、630
4.下面是一道有余数的整数除法算式:
A÷B=C……R,若B是最小的合数,C是最小的质数,则
A最大是( ),最小是( )。
问题:最小的合数是谁?
最小的质数又是谁?
R最大是几?最小呢?
质数和合数的意义
3
11
9
质数和合数的意义
3
(1)所有的奇数都是质数,所有的偶数都是合数。 ( )
(2)在自然数中,除了质数,就是合数。 ( )
(3)合数的因数比质数的因数多。 ( )
(4)两个质数的和是偶数。 ( )
问题:哪一句话是错误的,为什么?你能改正过来吗?
×
×
√
×
5. 判断。(对的画“√”,错的画“×”)
问题:什么样的数是质因数?什么是分解质因数?
分解质因数的方法
4
6.下面分解质因数对吗?不对的请改正。
(1)36=4×9 ( ) 改正:_______________
(2)10=1×2×5 ( ) 改正: _______________
(3)15=3+5+7 ( ) 改正: _______________
(4)18=3×6 ( ) 改正: _______________
×
36=2×2×3×3
×
10=2×5
×
15=3×5
×
18=3×3×2
1
变式练习
用排除法或列举法解决因数和倍数问题
2
4
号码疑团(根据要求写数)
综合运用2、5、3的倍数的特征解决问题
3
对奇数和偶数的运算性质的应用
1.一个数是36的因数,同时也是4的倍数,这个数可能是多少?
问题:解决这道题的关键是什么?
用排除法或列举法解决因数和倍数问题
1
方法一:先列举出36的因数,再排除不是4的倍数的数。
方法二:先写出36以内的4的倍数,再排除不是36的因数的数。
答:这个数可能是4、12或36。
用排除法或列举法解决因数和倍数问题
1
2.猜数游戏:
我既是18的因数,又是20以内3的倍数。
我可能是( )。
问题:你能用列举法解决这道题吗?
方法:先用列举法找出18的因数与20以内3的倍数,再找出
它们公共的数,这个公共的数即为所求的数。
3、6、9、18
3.既是2和5的倍数,又是3的倍数的最大两位数是( )。
问题:同时是2、5的倍数的数有什么特征?
3的倍数的特征是什么?
综合运用2、5、3的倍数的特征解决问题
2
90
总结:同时是2、5、3的倍数,这个数的个位上的数字一定
是0,其他数位上的数字相加的和必须是3的倍数。
综合运用2、5、3的倍数的特征解决问题
2
问题:这个三位数有一个因数是5是什么意思?
方法:先运用2、5、3的倍数的特征划出大致范围,再结合关
键字“最大”、“三位数”,即可找到符合要求的数。
990
4.一个三位数既是2的倍数又是3的倍数,并且有一个因数是5,这个三位数最大是( )。
5.火眼金睛辨对错:两个奇数的和一定是偶数。( )
问题:你能列举一些例子来验证这句话是否正确吗?
对奇数和偶数的运算性质的应用
3
方法指导:
偶数+偶数=偶数
偶数-偶数=偶数
偶数×偶数=偶数
奇数+奇数=偶数
奇数-奇数=偶数
奇数×奇数=奇数
偶数+奇数=奇数
偶数-奇数=奇数
偶数×奇数=偶数
√
号码疑团(根据要求写数)
4
问题:(1)谁既不是质数也不是合数?
(2)最小的质数是谁?
(3)谁是一位数中最大的合数?
6. 猜猜洋洋家的门牌号:△☆3※。
△是最小的质数;☆既不是质数,也不是合数;※是一位 数中最大的合数。
答:洋洋家的门牌号是:2139。
7.警察在查案时,发现了一个保险箱,保险箱设有六位数的密 码“ABCDEF”。
已知:A是10以内最大的质数;B的所有因数是1、2、4、8;C是最小的自然数;D只有一个因数;E既是质数,又是偶数;F 既是2的倍数,又是3的倍数。
这个六位数的密码是( )。
提示:先根据倍数、因数等定义逐步找出每个字母代表的数字,
再组成密码。
780126
号码疑团(根据要求写数)
4
拓展练习
1
2
3
解决一个数的因数问题
运用逆推法解决问题(分解质因数)
运用推理法解决倍数问题
1.妈妈让洋洋从放有32个苹果的箱子里拿苹果,不能一次拿完,
也不能1个1个地拿,并且每次拿的个数相同,拿到最后正好
一个不剩。洋洋共有几种拿法,每次各拿几个?
提示:先写出32的因数,看看有几个,再根据题意筛选即可。
解决一个数的因数问题
1
32的因数有1、2、4、8、16、32,共6个。
6-2=4(种)
答:洋洋共有4种拿法。每次各拿2个或4个或8个或16个。
2.幸福小学的舞蹈队有42人,编舞时需要把他们平均分成若
干个小队,每小队要求多于2人且少于8人,可以分成几个
小队?有几种分法?
问题:42的因数中哪些是符合题干要求的?
解决一个数的因数问题
1
42÷3=14(个)
答:可以分成14个、7个或6个舞蹈小队,有3种分法。
42÷6=7(个)
42÷7=6(个)
3.一筐桃子有若干个(少于65个),2个2个地数正好数完,5
个5个地数也正好数完。这筐桃子可能有多少个?
问题:(1)这筐桃子的个数有什么特点?
(2)既是2的倍数又是5的倍数的数有什么特征?
运用推理法解决倍数问题
2
答:这筐桃子可能有10个、20个、30个、40个、50个、60个。
4.学校组织四年级的学生参加植树活动,已经来了32人,至
少还要来( )人,才能正好分成5人一组。
解决一个数的因数问题
2
问题:(1)5的倍数的特征是什么?
(2)32至少加上几才是5的倍数?
3
5.975×935×972×( ),要使这个连乘算式的积的最后5
个数字都是0,括号内最小应填几?
方法指导:乘积的末尾数0的个数,取决于因数5和因数2的个
数,关键是先找出因数5和因数2的个数。
运用逆推法解决问题(分解质因数)
3
这三个数的乘积里面含有3个因数5和2个因数2,要使这个连乘算式的积的最后5个数字都是0,还缺少2个因数5和3个因数2,因此括号内最小应填2×2×2×5×5=200。
975=3×5×5×13
935=5×11×17
972=2×2×3×3×3×3×3
谢 谢 大 家
我学会了吗?
复习方法
复习内容
将整理的知识与同伴进行交流,相互补充,并展示整理结果。
回忆本单元所学知识,尝试归纳、整理,用自己喜欢的形式表示出来。
1
2
4
基础练习
找一个数的因数或倍数
分解质因数的方法
2、5、3的倍数的特征
3
质数和合数的意义
1. 连一连。
问题:怎样找一个数的因数或倍数?
找一个数的因数和倍数
1
48
2
3
4
6
8
12
16
18
24
36
36的因数
12的倍数
既是36的因数
又是12的倍数
1
(1)因为0.8×4=3.2,所以3.2是0.8的倍数。( )
(2)一个数的倍数一定比它的因数大。 ( )
(3)在48÷4=12中,48是12的倍数。 ( )
(4)1是所有非0自然数的因数。 ( )
2. 判断。(对的画“√”,错的画“×”)
问题:哪一句话是错误的,为什么?你能改正过来吗?
1
×
×
√
√
整数除法
不一定
找一个数的因数和倍数
2
3.从下列四张卡片中任选三张,按要求组成三位数。
2、5、3的倍数的特征
3
0
6
5
3的倍数:_____________________________________________
5的倍数: _____________________________________________
同时是2和3的倍数: ____________________________________
306、360、603、630
360、630、305、350、530、365、635、650、560、605
306、360、630
2
3.从下列四张卡片中任选三张,按要求组成三位数。
2、5、3的倍数的特征
3
0
6
5
问题:2、5、3的倍数的特征分别是什么?
同时是2和5的倍数: ____________________________________
同时是3和5的倍数: ____________________________________
同时是2、3和5的倍数: _________________________________
360、630、350、530、650、560
360、630
360、630
4.下面是一道有余数的整数除法算式:
A÷B=C……R,若B是最小的合数,C是最小的质数,则
A最大是( ),最小是( )。
问题:最小的合数是谁?
最小的质数又是谁?
R最大是几?最小呢?
质数和合数的意义
3
11
9
质数和合数的意义
3
(1)所有的奇数都是质数,所有的偶数都是合数。 ( )
(2)在自然数中,除了质数,就是合数。 ( )
(3)合数的因数比质数的因数多。 ( )
(4)两个质数的和是偶数。 ( )
问题:哪一句话是错误的,为什么?你能改正过来吗?
×
×
√
×
5. 判断。(对的画“√”,错的画“×”)
问题:什么样的数是质因数?什么是分解质因数?
分解质因数的方法
4
6.下面分解质因数对吗?不对的请改正。
(1)36=4×9 ( ) 改正:_______________
(2)10=1×2×5 ( ) 改正: _______________
(3)15=3+5+7 ( ) 改正: _______________
(4)18=3×6 ( ) 改正: _______________
×
36=2×2×3×3
×
10=2×5
×
15=3×5
×
18=3×3×2
1
变式练习
用排除法或列举法解决因数和倍数问题
2
4
号码疑团(根据要求写数)
综合运用2、5、3的倍数的特征解决问题
3
对奇数和偶数的运算性质的应用
1.一个数是36的因数,同时也是4的倍数,这个数可能是多少?
问题:解决这道题的关键是什么?
用排除法或列举法解决因数和倍数问题
1
方法一:先列举出36的因数,再排除不是4的倍数的数。
方法二:先写出36以内的4的倍数,再排除不是36的因数的数。
答:这个数可能是4、12或36。
用排除法或列举法解决因数和倍数问题
1
2.猜数游戏:
我既是18的因数,又是20以内3的倍数。
我可能是( )。
问题:你能用列举法解决这道题吗?
方法:先用列举法找出18的因数与20以内3的倍数,再找出
它们公共的数,这个公共的数即为所求的数。
3、6、9、18
3.既是2和5的倍数,又是3的倍数的最大两位数是( )。
问题:同时是2、5的倍数的数有什么特征?
3的倍数的特征是什么?
综合运用2、5、3的倍数的特征解决问题
2
90
总结:同时是2、5、3的倍数,这个数的个位上的数字一定
是0,其他数位上的数字相加的和必须是3的倍数。
综合运用2、5、3的倍数的特征解决问题
2
问题:这个三位数有一个因数是5是什么意思?
方法:先运用2、5、3的倍数的特征划出大致范围,再结合关
键字“最大”、“三位数”,即可找到符合要求的数。
990
4.一个三位数既是2的倍数又是3的倍数,并且有一个因数是5,这个三位数最大是( )。
5.火眼金睛辨对错:两个奇数的和一定是偶数。( )
问题:你能列举一些例子来验证这句话是否正确吗?
对奇数和偶数的运算性质的应用
3
方法指导:
偶数+偶数=偶数
偶数-偶数=偶数
偶数×偶数=偶数
奇数+奇数=偶数
奇数-奇数=偶数
奇数×奇数=奇数
偶数+奇数=奇数
偶数-奇数=奇数
偶数×奇数=偶数
√
号码疑团(根据要求写数)
4
问题:(1)谁既不是质数也不是合数?
(2)最小的质数是谁?
(3)谁是一位数中最大的合数?
6. 猜猜洋洋家的门牌号:△☆3※。
△是最小的质数;☆既不是质数,也不是合数;※是一位 数中最大的合数。
答:洋洋家的门牌号是:2139。
7.警察在查案时,发现了一个保险箱,保险箱设有六位数的密 码“ABCDEF”。
已知:A是10以内最大的质数;B的所有因数是1、2、4、8;C是最小的自然数;D只有一个因数;E既是质数,又是偶数;F 既是2的倍数,又是3的倍数。
这个六位数的密码是( )。
提示:先根据倍数、因数等定义逐步找出每个字母代表的数字,
再组成密码。
780126
号码疑团(根据要求写数)
4
拓展练习
1
2
3
解决一个数的因数问题
运用逆推法解决问题(分解质因数)
运用推理法解决倍数问题
1.妈妈让洋洋从放有32个苹果的箱子里拿苹果,不能一次拿完,
也不能1个1个地拿,并且每次拿的个数相同,拿到最后正好
一个不剩。洋洋共有几种拿法,每次各拿几个?
提示:先写出32的因数,看看有几个,再根据题意筛选即可。
解决一个数的因数问题
1
32的因数有1、2、4、8、16、32,共6个。
6-2=4(种)
答:洋洋共有4种拿法。每次各拿2个或4个或8个或16个。
2.幸福小学的舞蹈队有42人,编舞时需要把他们平均分成若
干个小队,每小队要求多于2人且少于8人,可以分成几个
小队?有几种分法?
问题:42的因数中哪些是符合题干要求的?
解决一个数的因数问题
1
42÷3=14(个)
答:可以分成14个、7个或6个舞蹈小队,有3种分法。
42÷6=7(个)
42÷7=6(个)
3.一筐桃子有若干个(少于65个),2个2个地数正好数完,5
个5个地数也正好数完。这筐桃子可能有多少个?
问题:(1)这筐桃子的个数有什么特点?
(2)既是2的倍数又是5的倍数的数有什么特征?
运用推理法解决倍数问题
2
答:这筐桃子可能有10个、20个、30个、40个、50个、60个。
4.学校组织四年级的学生参加植树活动,已经来了32人,至
少还要来( )人,才能正好分成5人一组。
解决一个数的因数问题
2
问题:(1)5的倍数的特征是什么?
(2)32至少加上几才是5的倍数?
3
5.975×935×972×( ),要使这个连乘算式的积的最后5
个数字都是0,括号内最小应填几?
方法指导:乘积的末尾数0的个数,取决于因数5和因数2的个
数,关键是先找出因数5和因数2的个数。
运用逆推法解决问题(分解质因数)
3
这三个数的乘积里面含有3个因数5和2个因数2,要使这个连乘算式的积的最后5个数字都是0,还缺少2个因数5和3个因数2,因此括号内最小应填2×2×2×5×5=200。
975=3×5×5×13
935=5×11×17
972=2×2×3×3×3×3×3
谢 谢 大 家
