数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 18:46:33 | ||
图片预览








文档简介
(共30张PPT)
1.1.1空间向量及其线性运算
1.理解空间向量的含义,能够区别于平面向量,懂得一些特殊向量如零向量和单位向量。理解相等向量和相反向量,后续进一步理解共面向量和异面向量。
2.掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解。培养数形结合思想,发展数学抽象等核心素养。
1.1.1空间向量及其线性运算学习目标
环节一 创设情境 引入课题
想象一个滑翔伞运动的场景,在滑翔过程中,飞行员受到来自不同方向、大小各异的力,如绳索的拉力、风力、重力等,这些力在同一平面内吗?
我们知道,力是既有大小又有方向的量,在数学上,我们把这些力称为什么?
[提示] 这些力不在同一平面内,在数学上,我们把这些力称为空间向量.
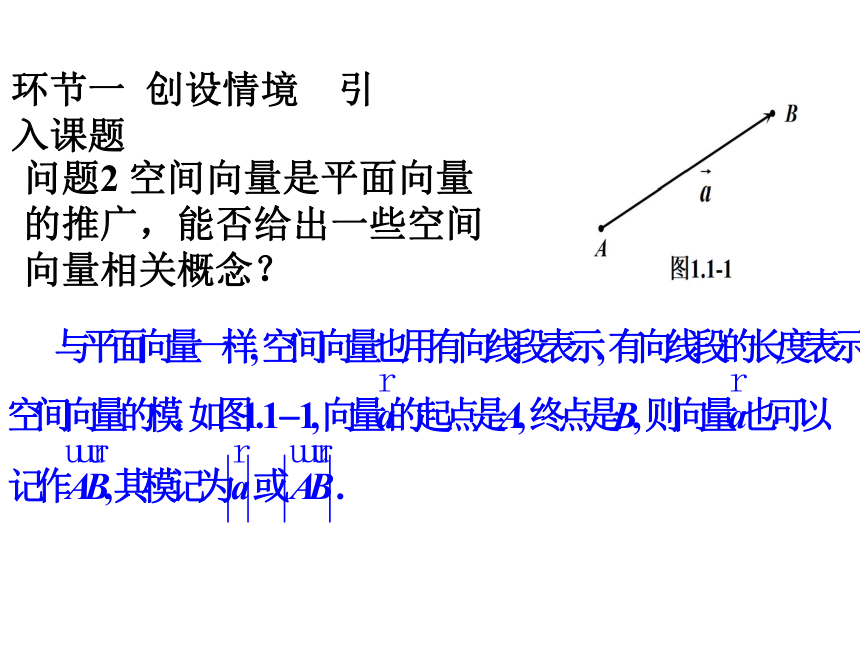
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量(space vector),空间向量的大小叫做空间向量的长度或模(modulus).
问题2 空间向量是平面向量的推广,能否给出一些空间向量相关概念?
环节一 创设情境 引入课题
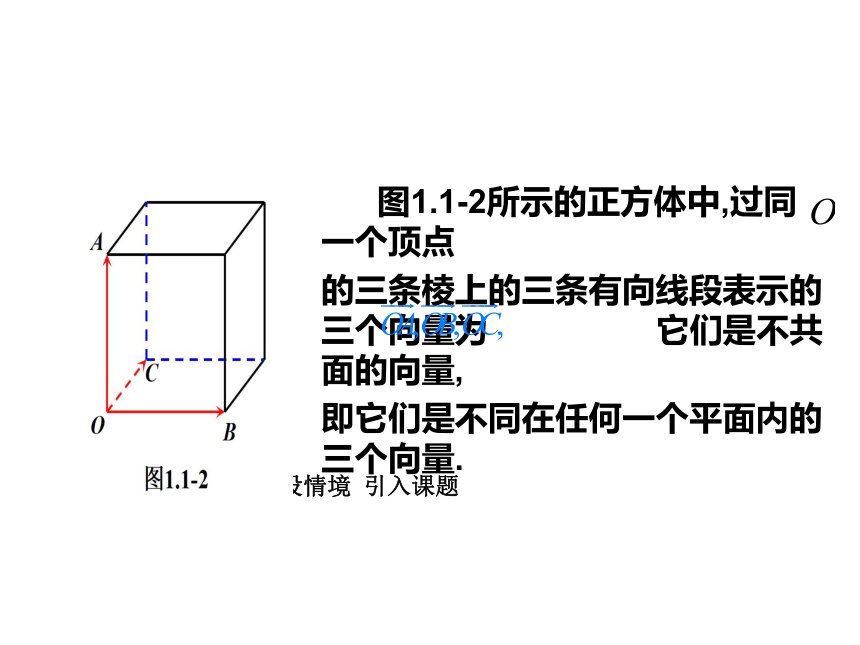
图1.1-2所示的正方体中,过同一个顶点
的三条棱上的三条有向线段表示的三个向量为 它们是不共面的向量,
即它们是不同在任何一个平面内的三个向量.
环节一 创设情境 引入课题
环节二 观察分析 感知概念
7
零向量的定义是什么?
单位向量的定义是什么?
相反向量的定义是什么?如何表示相反向量?
环节二 观察分析 感知概念
共线向量的定义是什么?
相等向量的定义是什么?
方向相同且模相等的向量叫做相等向量(equal vec tors).因此,在空间,同向且等长的有向线段表示同一向量或相等向量.
O
B
A
图1.1-3
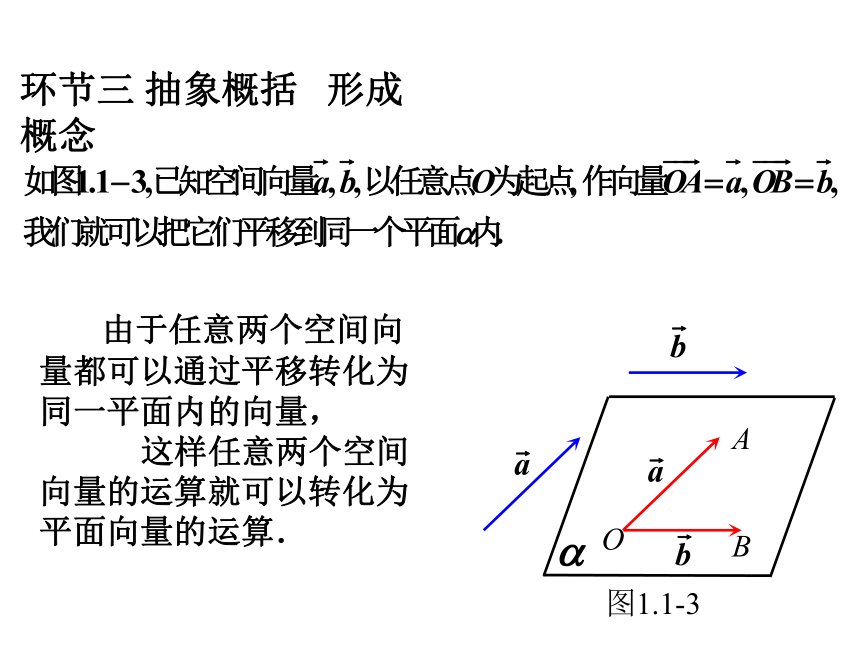
环节三 抽象概括 形成概念
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,
这样任意两个空间向量的运算就可以转化为平面向量的运算.
O
A
B
C
O
A
P
Q
M
N
图1.1-5
图1.1-4
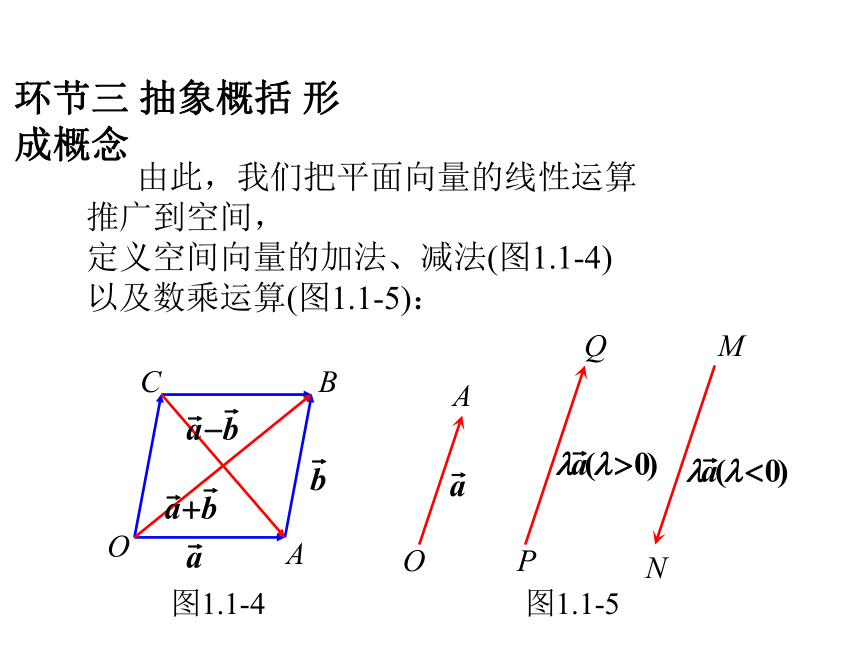
由此,我们把平面向量的线性运算推广到空间,
定义空间向量的加法、减法(图1.1-4)
以及数乘运算(图1.1-5):
环节三 抽象概括 形成概念
O
A
B
C
O
A
P
Q
M
N
环节四 辨析理解 深化概念
想一想,向量线性运算的结果,与向量起点的选择有关系吗?
你能证明这些运算律吗?证明结合律时,与证明平面向量的结合律有什么不同?
探究1
如图1.1-6, 在平行六面体 中, 分别标出 表示的向量.
从中你能体会向量加法运算的交换律和结 合律吗
一般地, 三个不共面的向量的和与这三个向量有什么关系
环节四 辨析理解 深化概念
A
B
C
D
图1.1-6
环节四 辨析理解 深化概念
A
B
C
D
图1.1-6
环节四 辨析理解 深化概念
O
P
图1.1-7
l
环节四 辨析理解 深化概念
如图1.1-8, 如果表示向量的有向线段 所在的直线 与 直线 平行 或重合,那么称向量 平行于直线 . 如果直线 平行于平面 或在平面 内,那么称向量 平行于平面 .
平行于同一个平面的向量,叫做共面向量 (coplanar vectors).
环节四 辨析理解 深化概念
O
A
l
图1.1-8
我们知道,任意两个空间向量总是共面的, 但三个空间向量既可能是共面的,也可能是不共面的.
环节四 辨析理解 深化概念
什么情况下三个空间向量共面呢?
环节四 辨析理解 深化概念
例1 如图1.1-9, 已知平行四边形 , 过平面 外一点 , 作射线 , 在四条射线上分别取点 , 使
求证: 四点共面.
环节五 概念应用 巩固内化
O
A
B
C
D
E
F
G
H
图1.1-9
O
A
B
C
D
E
F
G
H
图1.1-9
环节五 概念应用 巩固内化
O
A
B
C
D
E
F
G
H
图1.1-9
环节六 归纳总结 反思提升
本节课的学习我们知道向量是具有大小和方向的量,这一概念既适用于平面,也适用于空间.由于空间向量是平面 向量的推广,因此空间向量及其相关概念、空间向量的表示法等与平面向量都是一致的。
类比平面向量引入了空间向量及相关概念、空间 向量的表示、共线向量与相等向量,并类比平面向量的加减、数乘运算和运算律,引入空间向量 的加减、数乘运算和运算律,类比平面向量研究空间向量的共线、共面问题。
理解空间向量及相关概念,掌握空间向量的表示,掌握空间向量的加减、数乘运算及其运算律等内容,并能借助图形理解空间向量线性运算及其运算律的意义。
请同学们回顾本节课的学习内容,并回答下列问题:
1. 本节课学习的概念有哪些?
2. 在解决问题时,用到了哪些数学思想?
1.举出一些表示三个不同在一个平面内的向量的实例.
生活中的例子,如墙角的三条棱所在的直线可用于表示三个不同在一个平面内的向量.
环节七 目标检测,作业布置
A
B
C
D
E
F
第2题
A
B
C
D
图1.1-6
A
B
C
D
E
F
(第4题)
A
B
C
D
E
F
A
B
C
D
E
F
1.1.1空间向量及其线性运算
1.理解空间向量的含义,能够区别于平面向量,懂得一些特殊向量如零向量和单位向量。理解相等向量和相反向量,后续进一步理解共面向量和异面向量。
2.掌握空间向量的加法、减法和数乘等线性法则、以及结合律和交换律等运算律,并通过空间几何体加深对运算的理解。培养数形结合思想,发展数学抽象等核心素养。
1.1.1空间向量及其线性运算学习目标
环节一 创设情境 引入课题
想象一个滑翔伞运动的场景,在滑翔过程中,飞行员受到来自不同方向、大小各异的力,如绳索的拉力、风力、重力等,这些力在同一平面内吗?
我们知道,力是既有大小又有方向的量,在数学上,我们把这些力称为什么?
[提示] 这些力不在同一平面内,在数学上,我们把这些力称为空间向量.
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量(space vector),空间向量的大小叫做空间向量的长度或模(modulus).
问题2 空间向量是平面向量的推广,能否给出一些空间向量相关概念?
环节一 创设情境 引入课题
图1.1-2所示的正方体中,过同一个顶点
的三条棱上的三条有向线段表示的三个向量为 它们是不共面的向量,
即它们是不同在任何一个平面内的三个向量.
环节一 创设情境 引入课题
环节二 观察分析 感知概念
7
零向量的定义是什么?
单位向量的定义是什么?
相反向量的定义是什么?如何表示相反向量?
环节二 观察分析 感知概念
共线向量的定义是什么?
相等向量的定义是什么?
方向相同且模相等的向量叫做相等向量(equal vec tors).因此,在空间,同向且等长的有向线段表示同一向量或相等向量.
O
B
A
图1.1-3
环节三 抽象概括 形成概念
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,
这样任意两个空间向量的运算就可以转化为平面向量的运算.
O
A
B
C
O
A
P
Q
M
N
图1.1-5
图1.1-4
由此,我们把平面向量的线性运算推广到空间,
定义空间向量的加法、减法(图1.1-4)
以及数乘运算(图1.1-5):
环节三 抽象概括 形成概念
O
A
B
C
O
A
P
Q
M
N
环节四 辨析理解 深化概念
想一想,向量线性运算的结果,与向量起点的选择有关系吗?
你能证明这些运算律吗?证明结合律时,与证明平面向量的结合律有什么不同?
探究1
如图1.1-6, 在平行六面体 中, 分别标出 表示的向量.
从中你能体会向量加法运算的交换律和结 合律吗
一般地, 三个不共面的向量的和与这三个向量有什么关系
环节四 辨析理解 深化概念
A
B
C
D
图1.1-6
环节四 辨析理解 深化概念
A
B
C
D
图1.1-6
环节四 辨析理解 深化概念
O
P
图1.1-7
l
环节四 辨析理解 深化概念
如图1.1-8, 如果表示向量的有向线段 所在的直线 与 直线 平行 或重合,那么称向量 平行于直线 . 如果直线 平行于平面 或在平面 内,那么称向量 平行于平面 .
平行于同一个平面的向量,叫做共面向量 (coplanar vectors).
环节四 辨析理解 深化概念
O
A
l
图1.1-8
我们知道,任意两个空间向量总是共面的, 但三个空间向量既可能是共面的,也可能是不共面的.
环节四 辨析理解 深化概念
什么情况下三个空间向量共面呢?
环节四 辨析理解 深化概念
例1 如图1.1-9, 已知平行四边形 , 过平面 外一点 , 作射线 , 在四条射线上分别取点 , 使
求证: 四点共面.
环节五 概念应用 巩固内化
O
A
B
C
D
E
F
G
H
图1.1-9
O
A
B
C
D
E
F
G
H
图1.1-9
环节五 概念应用 巩固内化
O
A
B
C
D
E
F
G
H
图1.1-9
环节六 归纳总结 反思提升
本节课的学习我们知道向量是具有大小和方向的量,这一概念既适用于平面,也适用于空间.由于空间向量是平面 向量的推广,因此空间向量及其相关概念、空间向量的表示法等与平面向量都是一致的。
类比平面向量引入了空间向量及相关概念、空间 向量的表示、共线向量与相等向量,并类比平面向量的加减、数乘运算和运算律,引入空间向量 的加减、数乘运算和运算律,类比平面向量研究空间向量的共线、共面问题。
理解空间向量及相关概念,掌握空间向量的表示,掌握空间向量的加减、数乘运算及其运算律等内容,并能借助图形理解空间向量线性运算及其运算律的意义。
请同学们回顾本节课的学习内容,并回答下列问题:
1. 本节课学习的概念有哪些?
2. 在解决问题时,用到了哪些数学思想?
1.举出一些表示三个不同在一个平面内的向量的实例.
生活中的例子,如墙角的三条棱所在的直线可用于表示三个不同在一个平面内的向量.
环节七 目标检测,作业布置
A
B
C
D
E
F
第2题
A
B
C
D
图1.1-6
A
B
C
D
E
F
(第4题)
A
B
C
D
E
F
A
B
C
D
E
F
