人教A版(2019)必修第二册 10.3 随机事件、频率与概率 课件(17张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册 10.3 随机事件、频率与概率 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 19:07:39 | ||
图片预览






文档简介
(共17张PPT)
第十章 计数原理、概率、随机变量及其分布
第4节 随机事件、频率与概率
考试要求
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.了解两个互斥事件的概率加法公式.
知识梳理
(2)样本空间:全体样本点的集合,用Ω表示.
(1)样本点:随机试验E的每个可能的基本结果,用ω表示.
(3)随机事件(简称事件):样本空间Ω的子集. (必然事件,不可能事件)
2.频率与概率的关系:
(1)在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性;
(2)概率可看作频率理论上的期望值,它从数量上反映了随机事件发生的可能性的大小;是稳定值.
(3)一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即大量重复的试验,试验的次数越多,获得的数据越多,这时可以使用频率fn(A)估计概率P(A).
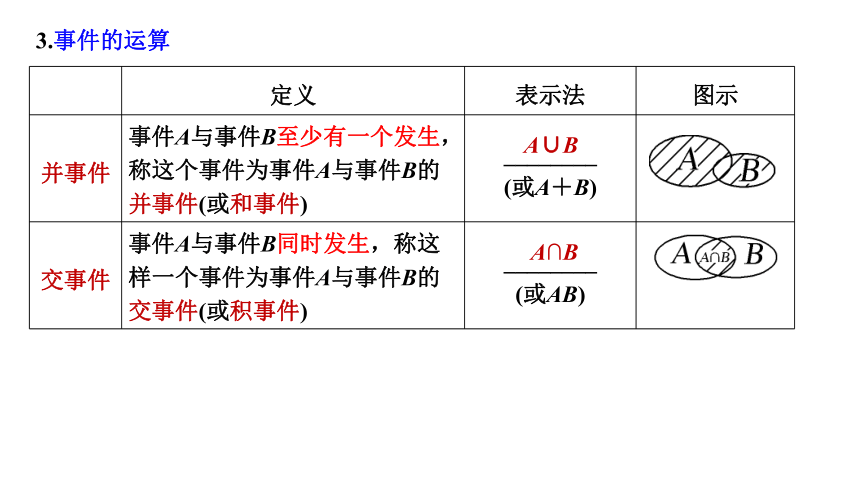
3.事件的运算
定义 表示法 图示
并事件 事件A与事件B至少有一个发生,称这个事件为事件A与事件B的并事件(或和事件) ________ (或A+B)
交事件 事件A与事件B同时发生,称这样一个事件为事件A与事件B的交事件(或积事件) ________ (或AB)
A∪B
A∩B
3.事件的关系
定义 表示法 图示
包含关系 若事件A发生,事件B________,称事件B包含事件A(或事件A包含于事件B) ________ (或A B)
互斥事件 如果事件A与事件B______________,称事件A与事件B互斥(或互不相容) 若A∩B= ,则A与B互斥
对立事件 如果事件A和事件B在任何一次试验中________________,称事件A与事件B互为对立,事件A的对立事件记为 若A∩B= ,且A∪B=Ω,则A与B对立
一定发生
B A
不能同时发生
有且仅有一个发生
对立事件一定是互斥事件,互斥事件不一定是对立事件
常用结论
考点一 随机事件的关系
1.(多选)若干个人站成排,其中不是互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
BCD
解析 排头只能有一人,因此“甲站排头”与“乙站排头”互斥,
而B,C,D中,甲、乙站位不一定在同一位置,可以同时发生,因此它们都不互斥.故选BCD.
2.在一次随机试验中,彼此互斥的事件A,B,C,D发生的概率分别是0.2,0.2,0.3,0.3,则下列说法正确的是( )
A.A∪B与C是互斥事件,也是对立事件
B.B∪C与D是互斥事件,也是对立事件
C.A∪C与B∪D是互斥事件,但不是对立事件
D.A与B∪C∪D是互斥事件,也是对立事件
D
考点一 随机事件的关系
考点一 随机事件的关系
3.(多选)口袋里装有1红,2白,3黄共6个除颜色外完全相同的小球,从中取出两个球,事件A=“取出的两个球同色”,B=“取出的两个球中至少有一个黄球”,C=“取出的两个球至少有一个白球”,D=“取出的两个球不同色”,E=“取出的两个球中至多有一个白球”.下列判断正确的是( )
A.A与D为对立事件 B.B与C是互斥事件
C.C与E是对立事件 D.P(C∪E)=1
AD
感悟提升
1.准确把握互斥事件与对立事件的概念:
(1)互斥事件是不可能同时发生的事件,但也可以同时不发生;
(2)对立事件是特殊的互斥事件,特殊在对立的两个事件不可能都不发生,
即有且仅有一个发生.
2.判别互斥事件、对立事件一般用定义判断,
不可能同时发生的两个事件为互斥事件;
两个事件,若有且仅有一个发生,则这两个事件为对立事件,
对立事件一定是互斥事件.
考点二 随机事件的频率与概率
例1 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.
例1 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
考点二 随机事件的频率与概率
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
(2)设六月份一天销售这种酸
奶的利润为Y(单位:元),当六月
份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
解 当这种酸奶一天的进货量为450瓶时,
若最高气温低于20,则
若最高气温位于区间[20,25),则
若最高气温不低于25,则
所以,利润Y的所有可能值为
因此Y大于零的概率的估计值为0.8.
训练1 (2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
解 由试加工产品等级的频数分布表知,
训练1 (2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
等级 A B C D
频数 28 17 34 21
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
解 甲分厂加工出来的100件产品的平均利润为
乙分厂加工出来的100件产品的平均利润为
比较甲、乙两分厂加工的产品的平均利润,厂家应选甲分厂承接加工业务.
考点三 互斥事件与对立事件的概率
例2 某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)1张奖券的中奖概率;
(2)1张奖券不中特等奖且不中一等奖的概率.
解 (1)设“1张奖券中奖”为事件M,则
∵A,B,C两两互斥,
(2)设“1张奖券既不中特等奖也不中一等奖”为事件N,
感悟提升
求:(1)至多2人排队等候的概率;
训练2 经统计,在某储蓄所一个营业窗口等候的人数相应的概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概率 0.1 0.16 0.3 0.3 0.1 0.04
(2)至少3人排队等候的概率.
解 (1)记“至多2人排队等候”为事件A,
(2)记“至少3人排队等候”为事件B,
第十章 计数原理、概率、随机变量及其分布
第4节 随机事件、频率与概率
考试要求
1.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.
2.了解两个互斥事件的概率加法公式.
知识梳理
(2)样本空间:全体样本点的集合,用Ω表示.
(1)样本点:随机试验E的每个可能的基本结果,用ω表示.
(3)随机事件(简称事件):样本空间Ω的子集. (必然事件,不可能事件)
2.频率与概率的关系:
(1)在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性;
(2)概率可看作频率理论上的期望值,它从数量上反映了随机事件发生的可能性的大小;是稳定值.
(3)一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即大量重复的试验,试验的次数越多,获得的数据越多,这时可以使用频率fn(A)估计概率P(A).
3.事件的运算
定义 表示法 图示
并事件 事件A与事件B至少有一个发生,称这个事件为事件A与事件B的并事件(或和事件) ________ (或A+B)
交事件 事件A与事件B同时发生,称这样一个事件为事件A与事件B的交事件(或积事件) ________ (或AB)
A∪B
A∩B
3.事件的关系
定义 表示法 图示
包含关系 若事件A发生,事件B________,称事件B包含事件A(或事件A包含于事件B) ________ (或A B)
互斥事件 如果事件A与事件B______________,称事件A与事件B互斥(或互不相容) 若A∩B= ,则A与B互斥
对立事件 如果事件A和事件B在任何一次试验中________________,称事件A与事件B互为对立,事件A的对立事件记为 若A∩B= ,且A∪B=Ω,则A与B对立
一定发生
B A
不能同时发生
有且仅有一个发生
对立事件一定是互斥事件,互斥事件不一定是对立事件
常用结论
考点一 随机事件的关系
1.(多选)若干个人站成排,其中不是互斥事件的是( )
A.“甲站排头”与“乙站排头”
B.“甲站排头”与“乙不站排尾”
C.“甲站排头”与“乙站排尾”
D.“甲不站排头”与“乙不站排尾”
BCD
解析 排头只能有一人,因此“甲站排头”与“乙站排头”互斥,
而B,C,D中,甲、乙站位不一定在同一位置,可以同时发生,因此它们都不互斥.故选BCD.
2.在一次随机试验中,彼此互斥的事件A,B,C,D发生的概率分别是0.2,0.2,0.3,0.3,则下列说法正确的是( )
A.A∪B与C是互斥事件,也是对立事件
B.B∪C与D是互斥事件,也是对立事件
C.A∪C与B∪D是互斥事件,但不是对立事件
D.A与B∪C∪D是互斥事件,也是对立事件
D
考点一 随机事件的关系
考点一 随机事件的关系
3.(多选)口袋里装有1红,2白,3黄共6个除颜色外完全相同的小球,从中取出两个球,事件A=“取出的两个球同色”,B=“取出的两个球中至少有一个黄球”,C=“取出的两个球至少有一个白球”,D=“取出的两个球不同色”,E=“取出的两个球中至多有一个白球”.下列判断正确的是( )
A.A与D为对立事件 B.B与C是互斥事件
C.C与E是对立事件 D.P(C∪E)=1
AD
感悟提升
1.准确把握互斥事件与对立事件的概念:
(1)互斥事件是不可能同时发生的事件,但也可以同时不发生;
(2)对立事件是特殊的互斥事件,特殊在对立的两个事件不可能都不发生,
即有且仅有一个发生.
2.判别互斥事件、对立事件一般用定义判断,
不可能同时发生的两个事件为互斥事件;
两个事件,若有且仅有一个发生,则这两个事件为对立事件,
对立事件一定是互斥事件.
考点二 随机事件的频率与概率
例1 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.
例1 某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
考点二 随机事件的频率与概率
最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
(2)设六月份一天销售这种酸
奶的利润为Y(单位:元),当六月
份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
解 当这种酸奶一天的进货量为450瓶时,
若最高气温低于20,则
若最高气温位于区间[20,25),则
若最高气温不低于25,则
所以,利润Y的所有可能值为
因此Y大于零的概率的估计值为0.8.
训练1 (2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
解 由试加工产品等级的频数分布表知,
训练1 (2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元、50元、20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
等级 A B C D
频数 28 17 34 21
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
解 甲分厂加工出来的100件产品的平均利润为
乙分厂加工出来的100件产品的平均利润为
比较甲、乙两分厂加工的产品的平均利润,厂家应选甲分厂承接加工业务.
考点三 互斥事件与对立事件的概率
例2 某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)1张奖券的中奖概率;
(2)1张奖券不中特等奖且不中一等奖的概率.
解 (1)设“1张奖券中奖”为事件M,则
∵A,B,C两两互斥,
(2)设“1张奖券既不中特等奖也不中一等奖”为事件N,
感悟提升
求:(1)至多2人排队等候的概率;
训练2 经统计,在某储蓄所一个营业窗口等候的人数相应的概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概率 0.1 0.16 0.3 0.3 0.1 0.04
(2)至少3人排队等候的概率.
解 (1)记“至多2人排队等候”为事件A,
(2)记“至少3人排队等候”为事件B,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
