人教A版(2019)必修第一册 3.1.1 函数的概念及其表示 课件(22张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 3.1.1 函数的概念及其表示 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 19:08:08 | ||
图片预览





文档简介
(共22张PPT)
3.1.1函数的概念及其表示
在初中我们已经接触过函数的概念,知道函数是刻画变量之间对应关系的数学模型和工具,你能举出一些函数的例子吗?
在一个变化过程中,如果有两个变量,,并且对于的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说是自变量, 是的函数.
函数的变量说
本节我们将在集合的基础上,用新的观点进一步学习函数的概念.
问题1:某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:)之间的关系可以表示为:
.
是的函数吗?
②时间 的变化范围是什么?路程 的变化范围是什么?
③有人说:“根据对应关系,这趟列车加速到350km/h后,运行1小时就前进了350km.”你认为这个说法正确吗?
问题2:某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么:
③工作天数的变化范围是什么?的变化范围是什么?
是他的函数吗?
问题1和问题2中的函数是同一个函数吗?
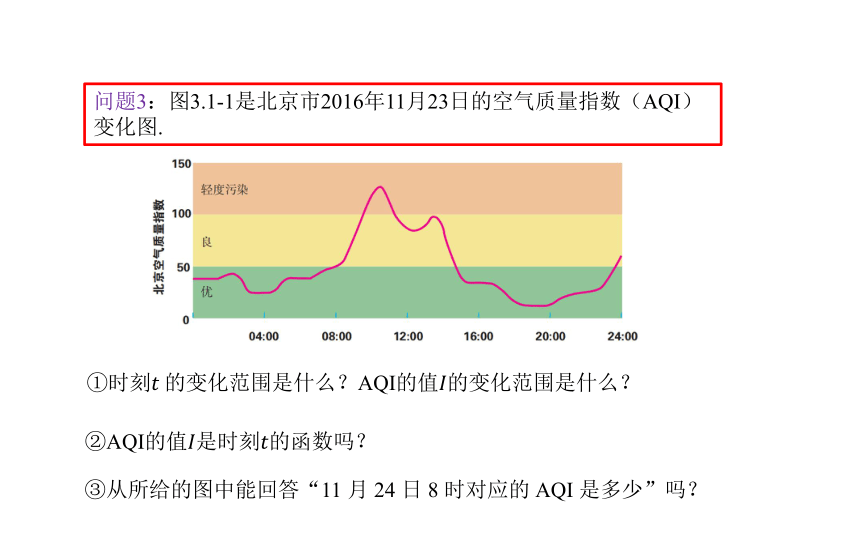
问题3:图3.1-1是北京市2016年11月23日的空气质量指数(AQI)变化图.
的值的变化范围是什么?
③从所给的图中能回答“11 月 24 日 8 时对应的 AQI 是多少”吗?
是时刻的函数吗?
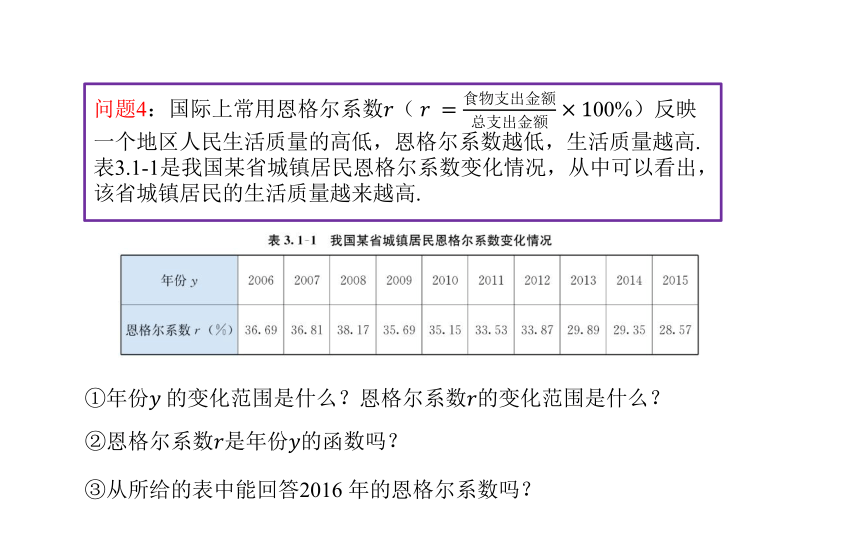
问题4:国际上常用恩格尔系数( 00%)反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高.表3.1-1是我国某省城镇居民恩格尔系数变化情况,从中可以看出,该省城镇居民的生活质量越来越高.
恩格尔系数的变化范围是什么?
③从所给的表中能回答2016 年的恩格尔系数吗?
是年份的函数吗?
上述问题1—问题4中函数有哪些共同特征?
(1)都包含两个非空数集,用 A, B 表示;
(2)都有一个对应关系;
(3)对应关系不同(解析式、图、表),对于数集 A中的任意一个数 x ,在数集 B 中都有唯一确定的数 y 和它对应.
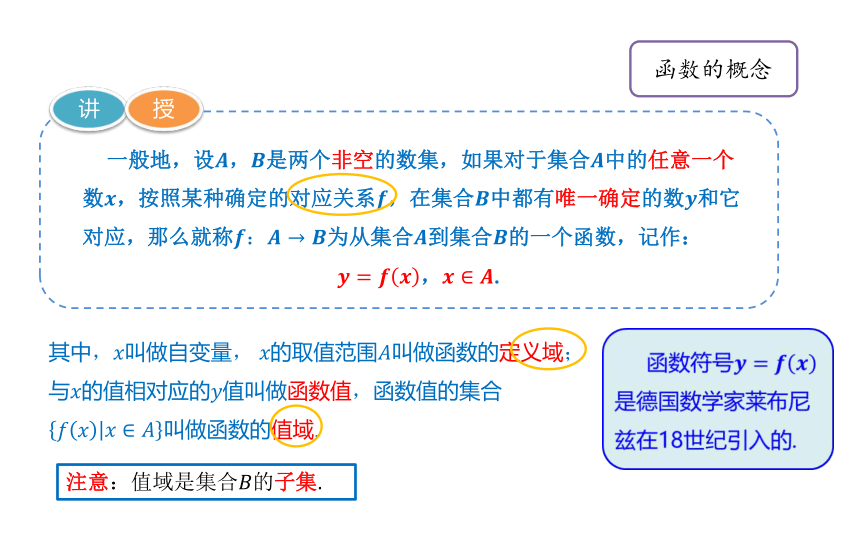
函数的概念
一般地,设,是两个非空的数集,如果对于集合中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作:
,.
其中,叫做自变量, 的取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.
注意:值域是集合的子集.
一、函数的三要素:
(1)定义域;(2)对应关系(3)值域
二、注意对应关系中的既可以是一个数,也可以是一个代数式.如则.并且自变量并不一定要用表示,有时候用,等.
三、表示当时的函数值,是一个常量.
一次函数、二次函数、反比例函数的定义域、对应关系和值域
③和④都可以称作半开半闭区间
各个区间的含义及表示方法如下表所示:
闭区间
开区间
左开右闭区间
左闭右开区间
常见区间的含义及表示方法如下表所示:
判断下列各题中的两个函数是否表示同一个函数
(1);(2)
(3) (4)
一个函数的构成要素为:定义域、对应关系和值域.
因为值域是由定义域和对应关系决定的,如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数就是同一个函数.
不关心对应过程,
只关心对应结果.
简单函数的定义域
求下列函数的定义域:
(1);(2)
分式分母不为0;
偶次根式被开方数非负;
函数中的不能为0.
注意:定义域必须用集合或者区间表示,若用区间表示数集,不能用“或”连接,应用并集符号“”连接.
复合函数的概念:
若函数的定义域为,函数的定义域为,值域为,则当时,称函数为和在上的复合函数,其中叫做中间变量,叫做内层函数,叫做外层函数.
注意:①定义域永远是的范围;
②同一个下,括号内作用对象范围相同.
*抽象函数或复合函数的定义域
1.已知函数的定义域为求函数的定义域.
2.已知函数的定义域为求函数的定义域.
3.已知函数的定义域为求函数的定义域.
归纳总结:
(1)若已知的定义域为则的定义域可由求出;
(2)若已知的定义域为,则的定义域为在的值域.
3.若( 为常数),,则的值为 .
2.已知函数 .
1.已知函数,那么集合中所含元素的个数为 .
教材P72复习巩固3.1第1、2题
定义域逆向求解
1.已知函数的定义域为,则 , .
2.已知函数的定义域为,则实数的取值范围是 .
求下列函数的值域
例2(1) ,;(2) ;
(3).
平方关系,二次配方
例3(1); .
抓住结构,换元凸显
例4(1)
,.
分离常数,分母范围
例1,.
例5(1)
判别式法,方程思想
例6(1)
绝对平方,反解表示
这节课你学到了什么?还有什么疑惑?
我的收获
我的疑惑
函数的概念:
函数三要素:
定义域、对应关系、值域
函数相同:定义域、对应关系相同
抽象函数或复合函数的定义域
函数值域的求法
3.1.1函数的概念及其表示
在初中我们已经接触过函数的概念,知道函数是刻画变量之间对应关系的数学模型和工具,你能举出一些函数的例子吗?
在一个变化过程中,如果有两个变量,,并且对于的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说是自变量, 是的函数.
函数的变量说
本节我们将在集合的基础上,用新的观点进一步学习函数的概念.
问题1:某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:)之间的关系可以表示为:
.
是的函数吗?
②时间 的变化范围是什么?路程 的变化范围是什么?
③有人说:“根据对应关系,这趟列车加速到350km/h后,运行1小时就前进了350km.”你认为这个说法正确吗?
问题2:某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么:
③工作天数的变化范围是什么?的变化范围是什么?
是他的函数吗?
问题1和问题2中的函数是同一个函数吗?
问题3:图3.1-1是北京市2016年11月23日的空气质量指数(AQI)变化图.
的值的变化范围是什么?
③从所给的图中能回答“11 月 24 日 8 时对应的 AQI 是多少”吗?
是时刻的函数吗?
问题4:国际上常用恩格尔系数( 00%)反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高.表3.1-1是我国某省城镇居民恩格尔系数变化情况,从中可以看出,该省城镇居民的生活质量越来越高.
恩格尔系数的变化范围是什么?
③从所给的表中能回答2016 年的恩格尔系数吗?
是年份的函数吗?
上述问题1—问题4中函数有哪些共同特征?
(1)都包含两个非空数集,用 A, B 表示;
(2)都有一个对应关系;
(3)对应关系不同(解析式、图、表),对于数集 A中的任意一个数 x ,在数集 B 中都有唯一确定的数 y 和它对应.
函数的概念
一般地,设,是两个非空的数集,如果对于集合中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作:
,.
其中,叫做自变量, 的取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.
注意:值域是集合的子集.
一、函数的三要素:
(1)定义域;(2)对应关系(3)值域
二、注意对应关系中的既可以是一个数,也可以是一个代数式.如则.并且自变量并不一定要用表示,有时候用,等.
三、表示当时的函数值,是一个常量.
一次函数、二次函数、反比例函数的定义域、对应关系和值域
③和④都可以称作半开半闭区间
各个区间的含义及表示方法如下表所示:
闭区间
开区间
左开右闭区间
左闭右开区间
常见区间的含义及表示方法如下表所示:
判断下列各题中的两个函数是否表示同一个函数
(1);(2)
(3) (4)
一个函数的构成要素为:定义域、对应关系和值域.
因为值域是由定义域和对应关系决定的,如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数就是同一个函数.
不关心对应过程,
只关心对应结果.
简单函数的定义域
求下列函数的定义域:
(1);(2)
分式分母不为0;
偶次根式被开方数非负;
函数中的不能为0.
注意:定义域必须用集合或者区间表示,若用区间表示数集,不能用“或”连接,应用并集符号“”连接.
复合函数的概念:
若函数的定义域为,函数的定义域为,值域为,则当时,称函数为和在上的复合函数,其中叫做中间变量,叫做内层函数,叫做外层函数.
注意:①定义域永远是的范围;
②同一个下,括号内作用对象范围相同.
*抽象函数或复合函数的定义域
1.已知函数的定义域为求函数的定义域.
2.已知函数的定义域为求函数的定义域.
3.已知函数的定义域为求函数的定义域.
归纳总结:
(1)若已知的定义域为则的定义域可由求出;
(2)若已知的定义域为,则的定义域为在的值域.
3.若( 为常数),,则的值为 .
2.已知函数 .
1.已知函数,那么集合中所含元素的个数为 .
教材P72复习巩固3.1第1、2题
定义域逆向求解
1.已知函数的定义域为,则 , .
2.已知函数的定义域为,则实数的取值范围是 .
求下列函数的值域
例2(1) ,;(2) ;
(3).
平方关系,二次配方
例3(1); .
抓住结构,换元凸显
例4(1)
,.
分离常数,分母范围
例1,.
例5(1)
判别式法,方程思想
例6(1)
绝对平方,反解表示
这节课你学到了什么?还有什么疑惑?
我的收获
我的疑惑
函数的概念:
函数三要素:
定义域、对应关系、值域
函数相同:定义域、对应关系相同
抽象函数或复合函数的定义域
函数值域的求法
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
