人教A版(2019)必修第一册 5.1.1 任意角 课件(21张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 5.1.1 任意角 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
§5.1.1 任意角
必修 第一册
第五章 三角函数
独立阅读,明确任务
问题1:请同学们先观察章头图并阅读第五章章引言,再回答如下问题:
(1)本章将要学习的函数是什么?
(2)这种函数主要可以解决我们实际生活中的哪类问题?你能举出具体例子吗?
(3)你能简单说说以前研究函数的过程与方法吗?
引导语
我们知道,现实世界中存在着各种各样的“周而复始”变化现象,圆周运动是这类现象的代表.
交流电
时钟
旋转木马
创设情境,引发思考
问题2 :如图1,⊙O上的点P以A为起点做逆时针方向的旋转,如何刻画点P的位置变化呢?
角
图1
分析事例,归纳特征
问题3 :我们以前所学角都在0°~360°的范围内,生活中有超出0°~360°角的例子吗?请你举例说明.
体操中“前空翻转体540度”
“后空翻转体720度”
如果要将钟表调快1.5小时,分针就会顺时针旋转540°,调慢1.5h,分针就会逆时针旋转540°
分析事例,归纳特征
(1)这些角的不同,体现在哪几个方面?
一是角的大小;二是旋转方向.
(2)根据旋转方向的不同,角可以分为哪几类?分别是什么?
通过阅读,获得概念
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角
规定:
说明:正角与负角是具有相反意义的旋转量.
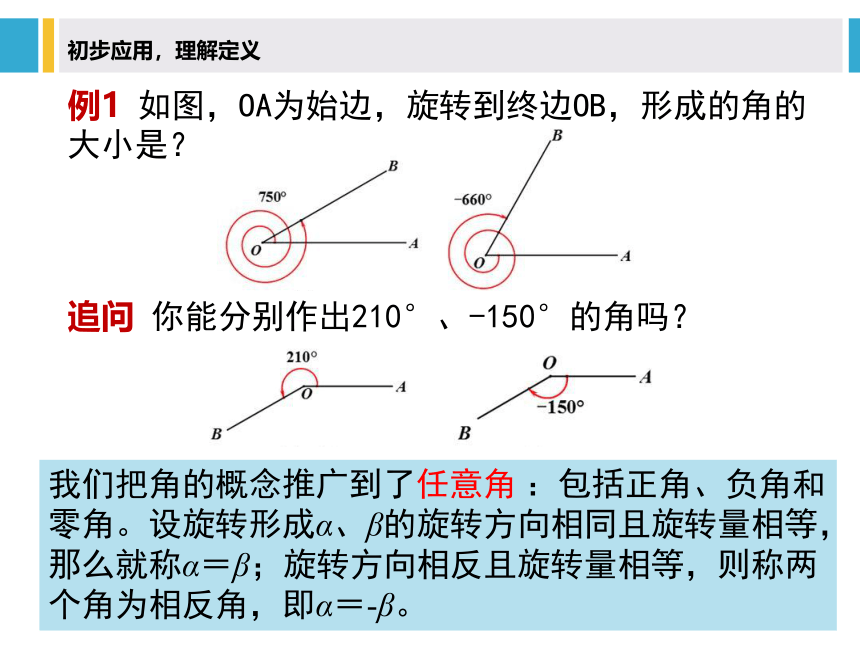
初步应用,理解定义
追问 你能分别作出210°、-150°的角吗?
例1 如图,OA为始边,旋转到终边OB,形成的角的大小是?
我们把角的概念推广到了任意角 :包括正角、负角和零角。设旋转形成α、β的旋转方向相同且旋转量相等,那么就称α=β;旋转方向相反且旋转量相等,则称两个角为相反角,即α=-β。
通过阅读,获得概念
问题4 我们在作460°角时,往往可以先作450°角然后再以450°角终边为始边再逆时针旋转10°得到。推广到一般如何表示α+β, α-β?
规定:把角α的终边旋转角β,这时终边所对应的角是α+β.
角的减法可以怎么做?
α-β=α+(-β)
研究分类,精致概念
问题5:
(1)在直角坐标系中研究角,其顶点和始边的位置是如何规定的?
(2)根据其终边位置的不同,又可以把角分为哪几类?
研究分类,精致概念
(2)把角的顶点放在平面直角坐标系的原点,角的始边与x轴的非负半轴重合,旋转该角,则其终边(除端点外)可能落在什么位置?
答:终边可能落在坐标轴上或四个象限内.
在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角:终边在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
终边
终边
o
终边
终边
思考:“锐角”“第一象限角”“小于90°的角”三者有何不同?
研究特殊位置,获得关系
问题6:在直角坐标系中画出30o,390o,-330o角。这三个角的终边有什么关系?
(1)终边相同的角有什么特点?
(2)试表示出与30o终边相同的角
研究特殊位置,获得关系
与α终边相同的角的一般形式为:
x
y
o
2.终边相同的角不一定相等;
相等的角终边一定相等;
终边相同的角有无数个,
它 们相差360°的整数倍.
1.α是任意的角
注意:
初步应用,理解关系
命题角度1 已知角求所在象限
例1:在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
初步应用,理解关系
命题角度2 已知终边求角的集合
例2:写出终边在y轴上的角的集合.
初步应用,理解关系
命题角度2 已知阴影部分的角的集合
例3 如图所示.
①写出终边落在射线OA,OB上的角的集合;
②写出终边落在阴影部分(包括边界)的角的集合.
初步应用,理解关系
命题角度2 已知阴影部分的角的集合
练3 已知角α的终边在图中阴影部分内,试指出角α的取值范围.
初步应用,理解关系
命题角度4 求半角所在象限
例5:若α是第一象限角,则 落在第几象限?
O
y
x
1
4
1
3
2
4
3
2
八卦图
初步应用,理解关系
命题角度4 求半角所在象限
变式1:若α是第一象限角,则2α落在第几象限?
变式2:若α是第一象限角,则 落在第几象限?
初步应用,理解关系
命题角度5 终边相同的角与对称等几何问题
小结
§5.1.1 任意角
必修 第一册
第五章 三角函数
独立阅读,明确任务
问题1:请同学们先观察章头图并阅读第五章章引言,再回答如下问题:
(1)本章将要学习的函数是什么?
(2)这种函数主要可以解决我们实际生活中的哪类问题?你能举出具体例子吗?
(3)你能简单说说以前研究函数的过程与方法吗?
引导语
我们知道,现实世界中存在着各种各样的“周而复始”变化现象,圆周运动是这类现象的代表.
交流电
时钟
旋转木马
创设情境,引发思考
问题2 :如图1,⊙O上的点P以A为起点做逆时针方向的旋转,如何刻画点P的位置变化呢?
角
图1
分析事例,归纳特征
问题3 :我们以前所学角都在0°~360°的范围内,生活中有超出0°~360°角的例子吗?请你举例说明.
体操中“前空翻转体540度”
“后空翻转体720度”
如果要将钟表调快1.5小时,分针就会顺时针旋转540°,调慢1.5h,分针就会逆时针旋转540°
分析事例,归纳特征
(1)这些角的不同,体现在哪几个方面?
一是角的大小;二是旋转方向.
(2)根据旋转方向的不同,角可以分为哪几类?分别是什么?
通过阅读,获得概念
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角
规定:
说明:正角与负角是具有相反意义的旋转量.
初步应用,理解定义
追问 你能分别作出210°、-150°的角吗?
例1 如图,OA为始边,旋转到终边OB,形成的角的大小是?
我们把角的概念推广到了任意角 :包括正角、负角和零角。设旋转形成α、β的旋转方向相同且旋转量相等,那么就称α=β;旋转方向相反且旋转量相等,则称两个角为相反角,即α=-β。
通过阅读,获得概念
问题4 我们在作460°角时,往往可以先作450°角然后再以450°角终边为始边再逆时针旋转10°得到。推广到一般如何表示α+β, α-β?
规定:把角α的终边旋转角β,这时终边所对应的角是α+β.
角的减法可以怎么做?
α-β=α+(-β)
研究分类,精致概念
问题5:
(1)在直角坐标系中研究角,其顶点和始边的位置是如何规定的?
(2)根据其终边位置的不同,又可以把角分为哪几类?
研究分类,精致概念
(2)把角的顶点放在平面直角坐标系的原点,角的始边与x轴的非负半轴重合,旋转该角,则其终边(除端点外)可能落在什么位置?
答:终边可能落在坐标轴上或四个象限内.
在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角:终边在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
终边
终边
o
终边
终边
思考:“锐角”“第一象限角”“小于90°的角”三者有何不同?
研究特殊位置,获得关系
问题6:在直角坐标系中画出30o,390o,-330o角。这三个角的终边有什么关系?
(1)终边相同的角有什么特点?
(2)试表示出与30o终边相同的角
研究特殊位置,获得关系
与α终边相同的角的一般形式为:
x
y
o
2.终边相同的角不一定相等;
相等的角终边一定相等;
终边相同的角有无数个,
它 们相差360°的整数倍.
1.α是任意的角
注意:
初步应用,理解关系
命题角度1 已知角求所在象限
例1:在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
初步应用,理解关系
命题角度2 已知终边求角的集合
例2:写出终边在y轴上的角的集合.
初步应用,理解关系
命题角度2 已知阴影部分的角的集合
例3 如图所示.
①写出终边落在射线OA,OB上的角的集合;
②写出终边落在阴影部分(包括边界)的角的集合.
初步应用,理解关系
命题角度2 已知阴影部分的角的集合
练3 已知角α的终边在图中阴影部分内,试指出角α的取值范围.
初步应用,理解关系
命题角度4 求半角所在象限
例5:若α是第一象限角,则 落在第几象限?
O
y
x
1
4
1
3
2
4
3
2
八卦图
初步应用,理解关系
命题角度4 求半角所在象限
变式1:若α是第一象限角,则2α落在第几象限?
变式2:若α是第一象限角,则 落在第几象限?
初步应用,理解关系
命题角度5 终边相同的角与对称等几何问题
小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
