人教A版(2019)选择性必修第三册 7.1.1 条件概率 课件(25张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 7.1.1 条件概率 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 19:11:40 | ||
图片预览






文档简介
7.1.1 条件概率
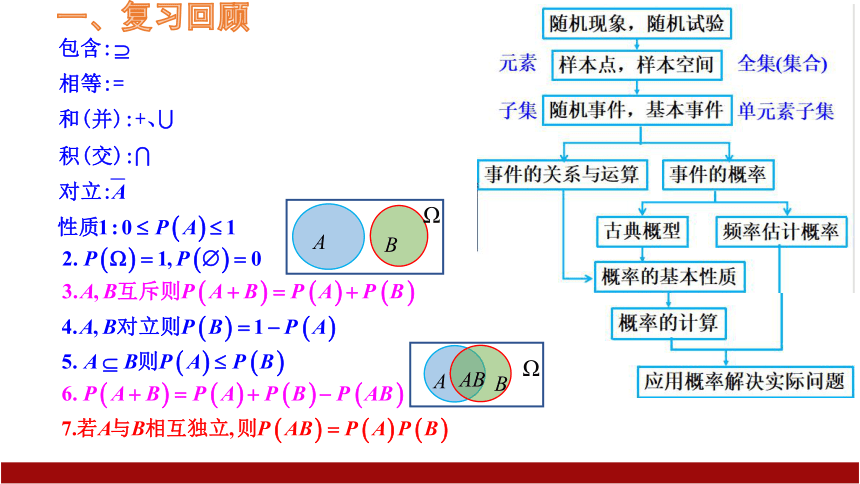
一、复习回顾
Ω
A
B
AB
Ω
A
B
知识回顾
2.古典概型:
3.古典概型概率计算公式:
1.概率是随机事件发生可能性大小的度量.
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型
3.事件A与B同时发生的事件叫做事件A与事件B的积事件,记为A∩B
(或AB);事件A与B至少有一个发生的事件叫做A与B的
和事件,记为 (或 );
思考:如果事件A与B不相互独立,如何求P(AB)呢?
下面我们从具体问题入手.
知识回顾
4.若AB为不可能事件,P(AB)=0,则事件A与事件B互斥;
5.若A发生不影响事件B的发生,则称事件A与事件B相互独立;
6.若事件A与事件B相互独立时,有P(AB)=P(A)P(B).
若事件A与B互斥,则:
已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
中奖的概率与抽奖的次序有关吗?
情境导入
0
探究新知
1
情境1
有4个相同的球,分别标有数字1,2,3,4,从中不放回的
随机取两次,每次取1个球,A=“第一次取出的球的数字是1”,
B=“第二次取出的球的数字是2”。
(1)求P(A),P(B).
(3)如果事件A已经发生,求事件B发生的概率.
缩小样本空间
(2)事件A,B是否相互独立?
古典概型:
相互独立:
体验新知
情境2
春节期间,妈妈带着C同学去朋友家做客,妈妈说她这个朋友有两个孩子。
闲谈时正巧碰到她的女儿回家.于是C同学在想,另一个孩子也是女孩的可能性有多大呢?是50%的概率吗?你能帮她分析一下吗?
(1)两个孩子都是女孩的概率? 设 =“两个孩子都是女孩”
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
条件A
“若事件A发生,则事件B发生的概率为多少”
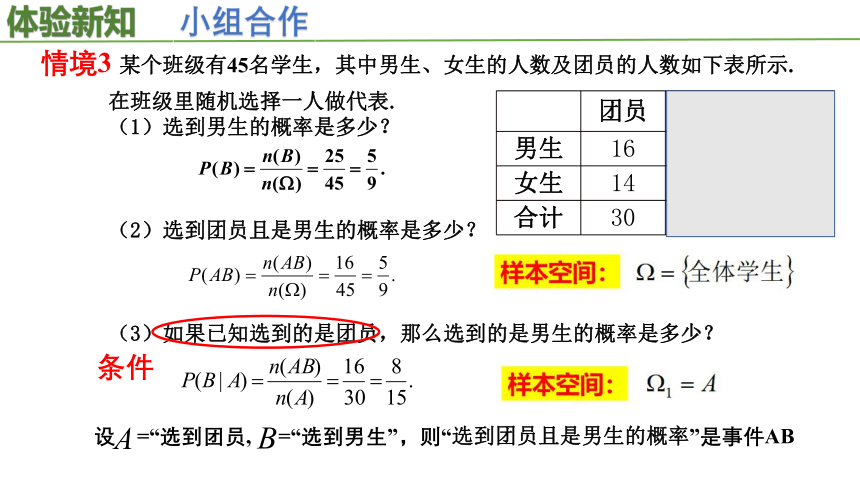
情境3 某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}
团员
非团员
合计
男生
16
9
25
女生
14
6
20
合计
30
15
45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)选到团员且是男生的概率是多少?
(3)如果已知选到的是团员,那么选到的是男生的概率是多少?
条件
设 =“选到团员, =“选到男生”,则“选到团员且是男生的概率”是事件AB
体验新知
小组合作
这个结论对于一般的古典概型仍然成立。
A
B
AB
Ω
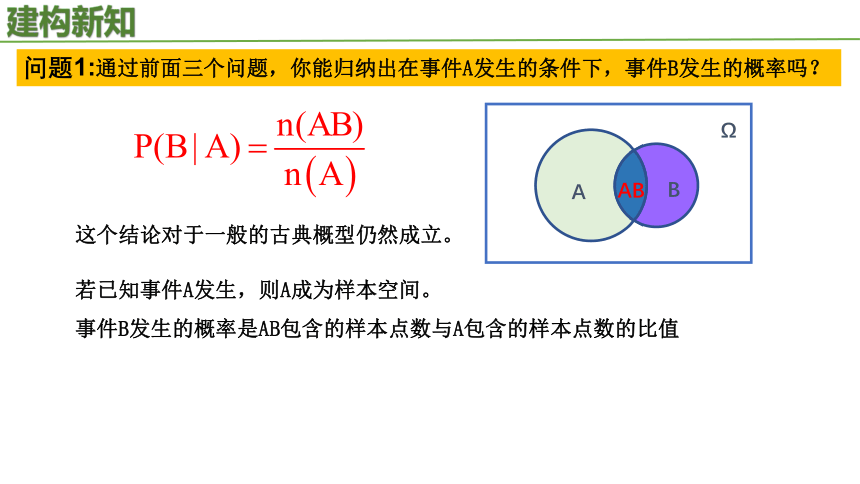
问题1:通过前面三个问题,你能归纳出在事件A发生的条件下,事件B发生的概率吗?
建构新知
若已知事件A发生,则A成为样本空间。
事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值
深入研究
问题2:你能发现 的联系吗?
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率。
条件概率
读作:在事件A发生的条件下事件B发生的概率
乘法公式
3
思考:对于任意两个事件????与????,如果已知????(????)与????(????|????),如何计算????(????????)呢?
?
有4个相同的球,分别标有数字1,2,3,4,从中不放回的
随机取两次,每次取1个球,A=“第一次取出的球的数字是1”,
B=“第二次取出的球的数字是2”。
求P(AB).
?问题3
深化概念
问题3:对于任意两个事件A与B,如果已知 ,如何计算 呢?
由条件概率 可得:
对于任意两个事件 与 ,若 ,
概率乘法公式
因为
所以
因为
所以
如果 与 相等,那么事件 与 应满足什么关系?为什么?
新旧辨析
特殊
P(A∪B)=P(A)+P(B)-P(AB)
当事件A与事件B不互斥时:
A
B
AB
Ω
典例分析
4
例1?在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.
求:(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
问题4:你能归纳条件概率的求法和步骤吗?
条件概率的计算方法
Ω
A
B
AB
从5道题中不放回地依次抽取2道的事件数为
根据分步乘法计数原理,
所以
“第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率.又
所以
例1:在5道题中有3道代数题和2道几何题,每次从中随机抽出1道题,
抽出的题不再放回.求第1次抽到代数题的条件下,第2次抽到几何题的概率.
解:设 =“第1次抽到代数题, =“第2次抽到几何题”,
则第1次抽到代数题且第2次都抽到几何题为事件 .
1.用字母表示有关事件
2.求相关量
3.代入公式求
解条件概率的一般步骤
典例分析
4
例2 良渚和仁和都是余杭区的两个街道,已知3月良渚下雨的概率为20%,仁和下雨的概率为18%,两地同时下雨的概率为12%,则
(1)良渚下雨的条件下,仁和也下雨的概率?
(2)仁和下雨的条件下,良渚也下雨的概率?
深化概念—条件概率是概率
问题5:条件概率是缩小了样本空间的概率,你能根据概率的性质得到
条件概率的性质吗?
性质3 如果事件C与事件B互斥, 那么
P(B∪C)=P(B)+P(C)
性质1 对任意的事件A,都有0 ≤ P(A) ≤1.
性质2 P(Ω)=1,P(Φ)=0.
性质4 如果事件B与事件 互为对立事件, 那么
P(B)=1- P( )
例3 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗?
解:
用A,B,C分别表示甲、乙、丙中奖的事件,则
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例4 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(2) 如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
(2) 设B=“最后1位密码为偶数”,则
说 明:
概率P(B|A)与P(AB)的区别与联系:
联系:事件A, B都发生了.
区别:
(1) 在P(B|A)中,事件A, B发生有时间上的差异,A先B后;在P(AB)中,事件A, B同时发生.
(2) 样本空间不同,在P(B|A)中,事件A成为样本空间;在P(AB)中,样本空间仍为Ω. 因此有P(B|A) ≥ P(AB).
请同学们带着以下问题,回顾本节课的研究过程:
1.本节课学习了哪些知识?我们是怎样研究的?
2.通过本节课的学习,你对条件概率有哪些认识、收获和感悟?
与前面学习的概率有哪些区别和联系?
反思提高
条件概率的性质
条件概率
两种方法
乘法公式
A、B独立
古典概型
复杂随机事件
简单随机事件
转化
谢谢聆听
一、复习回顾
Ω
A
B
AB
Ω
A
B
知识回顾
2.古典概型:
3.古典概型概率计算公式:
1.概率是随机事件发生可能性大小的度量.
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型(classical models of probability),简称古典概型
3.事件A与B同时发生的事件叫做事件A与事件B的积事件,记为A∩B
(或AB);事件A与B至少有一个发生的事件叫做A与B的
和事件,记为 (或 );
思考:如果事件A与B不相互独立,如何求P(AB)呢?
下面我们从具体问题入手.
知识回顾
4.若AB为不可能事件,P(AB)=0,则事件A与事件B互斥;
5.若A发生不影响事件B的发生,则称事件A与事件B相互独立;
6.若事件A与事件B相互独立时,有P(AB)=P(A)P(B).
若事件A与B互斥,则:
已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
中奖的概率与抽奖的次序有关吗?
情境导入
0
探究新知
1
情境1
有4个相同的球,分别标有数字1,2,3,4,从中不放回的
随机取两次,每次取1个球,A=“第一次取出的球的数字是1”,
B=“第二次取出的球的数字是2”。
(1)求P(A),P(B).
(3)如果事件A已经发生,求事件B发生的概率.
缩小样本空间
(2)事件A,B是否相互独立?
古典概型:
相互独立:
体验新知
情境2
春节期间,妈妈带着C同学去朋友家做客,妈妈说她这个朋友有两个孩子。
闲谈时正巧碰到她的女儿回家.于是C同学在想,另一个孩子也是女孩的可能性有多大呢?是50%的概率吗?你能帮她分析一下吗?
(1)两个孩子都是女孩的概率? 设 =“两个孩子都是女孩”
(2)如果有1个孩子是女孩,那么两个孩子都是女孩的概率又是多少?
条件A
“若事件A发生,则事件B发生的概率为多少”
情境3 某个班级有45名学生,其中男生、女生的人数及团员的人数如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}
团员
非团员
合计
男生
16
9
25
女生
14
6
20
合计
30
15
45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)选到团员且是男生的概率是多少?
(3)如果已知选到的是团员,那么选到的是男生的概率是多少?
条件
设 =“选到团员, =“选到男生”,则“选到团员且是男生的概率”是事件AB
体验新知
小组合作
这个结论对于一般的古典概型仍然成立。
A
B
AB
Ω
问题1:通过前面三个问题,你能归纳出在事件A发生的条件下,事件B发生的概率吗?
建构新知
若已知事件A发生,则A成为样本空间。
事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值
深入研究
问题2:你能发现 的联系吗?
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率。
条件概率
读作:在事件A发生的条件下事件B发生的概率
乘法公式
3
思考:对于任意两个事件????与????,如果已知????(????)与????(????|????),如何计算????(????????)呢?
?
有4个相同的球,分别标有数字1,2,3,4,从中不放回的
随机取两次,每次取1个球,A=“第一次取出的球的数字是1”,
B=“第二次取出的球的数字是2”。
求P(AB).
?问题3
深化概念
问题3:对于任意两个事件A与B,如果已知 ,如何计算 呢?
由条件概率 可得:
对于任意两个事件 与 ,若 ,
概率乘法公式
因为
所以
因为
所以
如果 与 相等,那么事件 与 应满足什么关系?为什么?
新旧辨析
特殊
P(A∪B)=P(A)+P(B)-P(AB)
当事件A与事件B不互斥时:
A
B
AB
Ω
典例分析
4
例1?在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.
求:(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
问题4:你能归纳条件概率的求法和步骤吗?
条件概率的计算方法
Ω
A
B
AB
从5道题中不放回地依次抽取2道的事件数为
根据分步乘法计数原理,
所以
“第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率.又
所以
例1:在5道题中有3道代数题和2道几何题,每次从中随机抽出1道题,
抽出的题不再放回.求第1次抽到代数题的条件下,第2次抽到几何题的概率.
解:设 =“第1次抽到代数题, =“第2次抽到几何题”,
则第1次抽到代数题且第2次都抽到几何题为事件 .
1.用字母表示有关事件
2.求相关量
3.代入公式求
解条件概率的一般步骤
典例分析
4
例2 良渚和仁和都是余杭区的两个街道,已知3月良渚下雨的概率为20%,仁和下雨的概率为18%,两地同时下雨的概率为12%,则
(1)良渚下雨的条件下,仁和也下雨的概率?
(2)仁和下雨的条件下,良渚也下雨的概率?
深化概念—条件概率是概率
问题5:条件概率是缩小了样本空间的概率,你能根据概率的性质得到
条件概率的性质吗?
性质3 如果事件C与事件B互斥, 那么
P(B∪C)=P(B)+P(C)
性质1 对任意的事件A,都有0 ≤ P(A) ≤1.
性质2 P(Ω)=1,P(Φ)=0.
性质4 如果事件B与事件 互为对立事件, 那么
P(B)=1- P( )
例3 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗?
解:
用A,B,C分别表示甲、乙、丙中奖的事件,则
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例4 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(2) 如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
(2) 设B=“最后1位密码为偶数”,则
说 明:
概率P(B|A)与P(AB)的区别与联系:
联系:事件A, B都发生了.
区别:
(1) 在P(B|A)中,事件A, B发生有时间上的差异,A先B后;在P(AB)中,事件A, B同时发生.
(2) 样本空间不同,在P(B|A)中,事件A成为样本空间;在P(AB)中,样本空间仍为Ω. 因此有P(B|A) ≥ P(AB).
请同学们带着以下问题,回顾本节课的研究过程:
1.本节课学习了哪些知识?我们是怎样研究的?
2.通过本节课的学习,你对条件概率有哪些认识、收获和感悟?
与前面学习的概率有哪些区别和联系?
反思提高
条件概率的性质
条件概率
两种方法
乘法公式
A、B独立
古典概型
复杂随机事件
简单随机事件
转化
谢谢聆听
