人教A版(2019)选择性必修第一册 1.1.1 空间向量及其线性运算 课件(28张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 1.1.1 空间向量及其线性运算 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 19:16:23 | ||
图片预览




文档简介
(共28张PPT)
空间向量及其线性运算
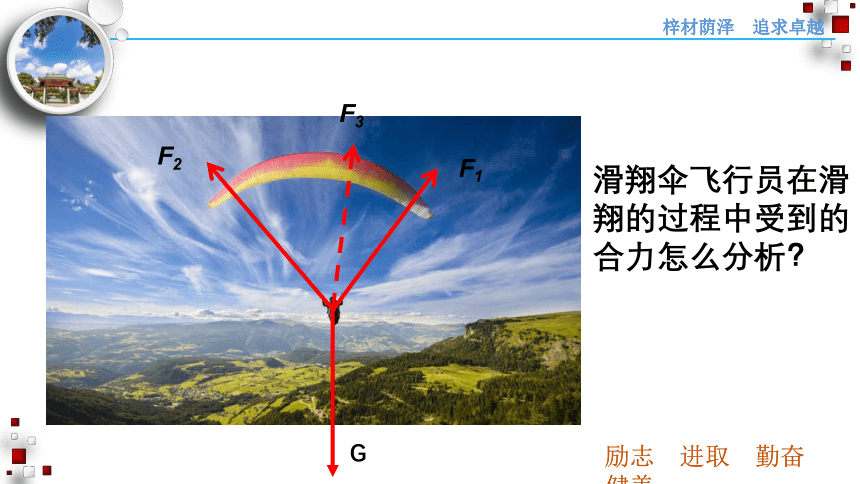
F1
F2
F3
G
滑翔伞飞行员在滑翔的过程中受到的合力怎么分析?
起点
终点
概念
与向量a长度相等而方向相反的向量,叫做a的相反向量
空间向量的相关概念
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线
互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
∥
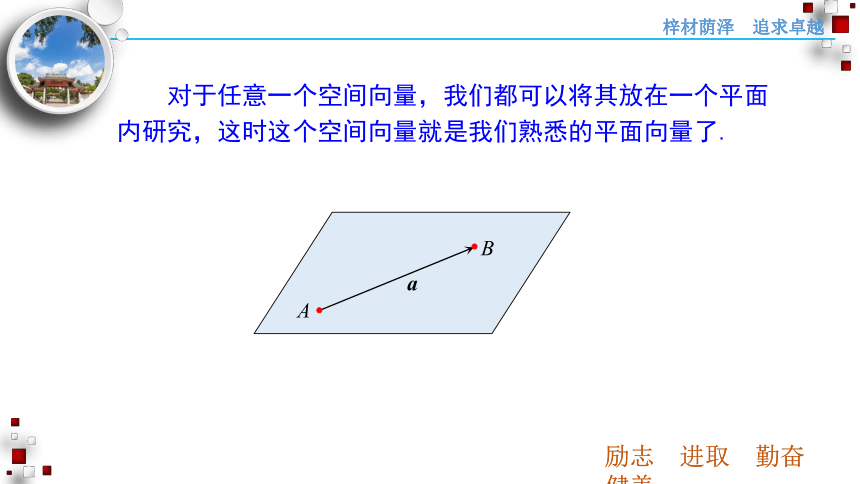
A
B
a
对于任意一个空间向量,我们都可以将其放在一个平面内研究,这时这个空间向量就是我们熟悉的平面向量了.
α
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.
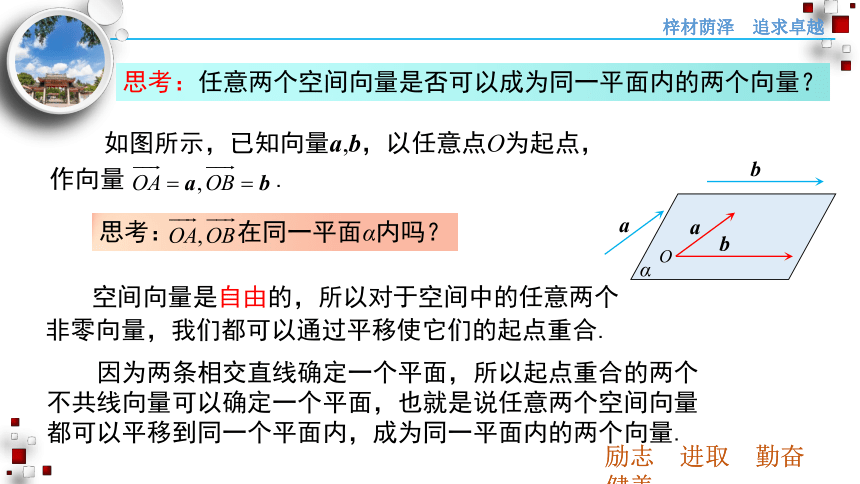
如图所示,已知向量a,b,以任意点O为起点,作向量 .
思考: 在同一平面α内吗?
思考:任意两个空间向量是否可以成为同一平面内的两个向量?
b
a
O
b
a
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
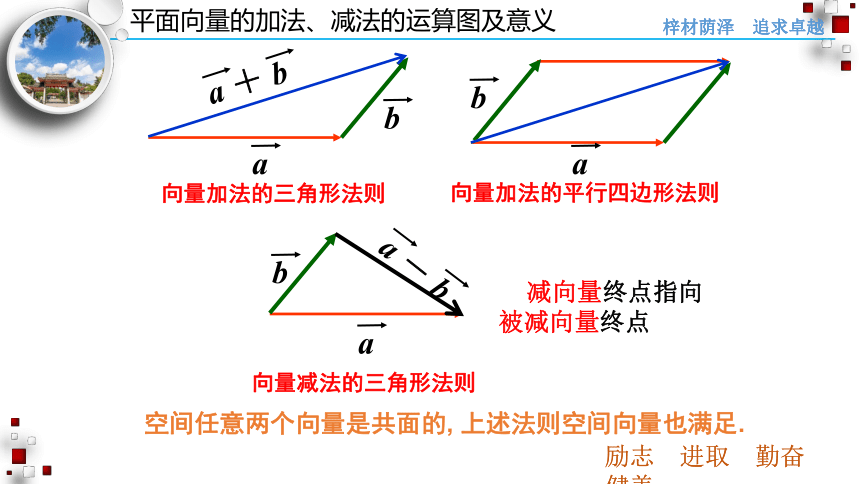
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
减向量终点指向被减向量终点
空间任意两个向量是共面的, 上述法则空间向量也满足.
平面向量的加法、减法的运算图及意义
三角形法则或平行四边形法则
三角形法则
空间向量的加法、减法及数乘运算的定义
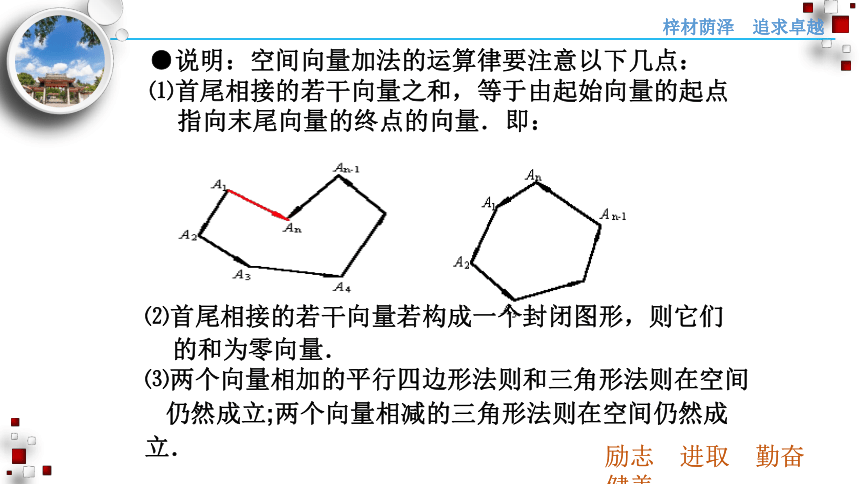
●说明:空间向量加法的运算律要注意以下几点:
⑴首尾相接的若干向量之和,等于由起始向量的起点
指向末尾向量的终点的向量.即:
⑵首尾相接的若干向量若构成一个封闭图形,则它们
的和为零向量.
⑶两个向量相加的平行四边形法则和三角形法则在空间
仍然成立;两个向量相减的三角形法则在空间仍然成立.
5 空间向量加法与数乘向量有如下运算律:
(1)加法交换律: ;
(2)加法结合律: ;
(3)数乘分配律: ;
(4)数乘结合律: .
b
a
b
a
向量加法交换律:
空间向量的运算律
C
'
B
'
A
'
D
'
D
A
B
C
注②: 始点相同的三个不共面向量之和, 等于以这三个向量为
棱的平行六面体的以公共始点为始点的对角线所示向量
注①:有限个向量求和,交换相加向量的顺序,其和不变。
如果 l 为经过已知点O且平行于已知
非零向量a的直线,那么对直线上任一点P,点P在直线l上的充要条件是存在实数t,满足等式
向量a叫做直线 l 的方向向量.
→
→
l
O
P
a
方向向量
推论1
如果 l 为经过已知点O且平行于已知
非零向量a的直线,那么对任一点P,点
P在直线l上的充要条件是存在实数t,满
足等式
向量a叫做直线 l 的方向向量.
→
①
OP=OA+ta.
→
→
l
O
P
A
a
推论2
如果 l 为经过已知点A且平行于已知
非零向量a的直线,那么对任一点O,点
P在直线l上的充要条件是存在实数t,满
足等式
向量a叫做直线 l 的方向向量.
→
①
OP=OA+ta.
→
→
则①可化成
OP=OA+tAB ,
l
O
P
A
a
B
在l上取AB=a,
OP=(1-t)OA+tOB .
得证.
A
M
C
G
D
B
D
ABD
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A’
B’
C’
D’
E
F
回顾
1 空间向量及其线性运算:
(1)空间向量的概念:定义;表示法;相关概念
(2)空间向量的线性运算:加、减、数乘运算及其运算律
(3)线性运算的应用:直线的方向向量;向量共面
2 类比平面向量的研究方法:
推广
谢
谢
聆
听
空间向量及其线性运算
F1
F2
F3
G
滑翔伞飞行员在滑翔的过程中受到的合力怎么分析?
起点
终点
概念
与向量a长度相等而方向相反的向量,叫做a的相反向量
空间向量的相关概念
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线
互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
∥
A
B
a
对于任意一个空间向量,我们都可以将其放在一个平面内研究,这时这个空间向量就是我们熟悉的平面向量了.
α
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.
如图所示,已知向量a,b,以任意点O为起点,作向量 .
思考: 在同一平面α内吗?
思考:任意两个空间向量是否可以成为同一平面内的两个向量?
b
a
O
b
a
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
减向量终点指向被减向量终点
空间任意两个向量是共面的, 上述法则空间向量也满足.
平面向量的加法、减法的运算图及意义
三角形法则或平行四边形法则
三角形法则
空间向量的加法、减法及数乘运算的定义
●说明:空间向量加法的运算律要注意以下几点:
⑴首尾相接的若干向量之和,等于由起始向量的起点
指向末尾向量的终点的向量.即:
⑵首尾相接的若干向量若构成一个封闭图形,则它们
的和为零向量.
⑶两个向量相加的平行四边形法则和三角形法则在空间
仍然成立;两个向量相减的三角形法则在空间仍然成立.
5 空间向量加法与数乘向量有如下运算律:
(1)加法交换律: ;
(2)加法结合律: ;
(3)数乘分配律: ;
(4)数乘结合律: .
b
a
b
a
向量加法交换律:
空间向量的运算律
C
'
B
'
A
'
D
'
D
A
B
C
注②: 始点相同的三个不共面向量之和, 等于以这三个向量为
棱的平行六面体的以公共始点为始点的对角线所示向量
注①:有限个向量求和,交换相加向量的顺序,其和不变。
如果 l 为经过已知点O且平行于已知
非零向量a的直线,那么对直线上任一点P,点P在直线l上的充要条件是存在实数t,满足等式
向量a叫做直线 l 的方向向量.
→
→
l
O
P
a
方向向量
推论1
如果 l 为经过已知点O且平行于已知
非零向量a的直线,那么对任一点P,点
P在直线l上的充要条件是存在实数t,满
足等式
向量a叫做直线 l 的方向向量.
→
①
OP=OA+ta.
→
→
l
O
P
A
a
推论2
如果 l 为经过已知点A且平行于已知
非零向量a的直线,那么对任一点O,点
P在直线l上的充要条件是存在实数t,满
足等式
向量a叫做直线 l 的方向向量.
→
①
OP=OA+ta.
→
→
则①可化成
OP=OA+tAB ,
l
O
P
A
a
B
在l上取AB=a,
OP=(1-t)OA+tOB .
得证.
A
M
C
G
D
B
D
ABD
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A’
B’
C’
D’
E
F
回顾
1 空间向量及其线性运算:
(1)空间向量的概念:定义;表示法;相关概念
(2)空间向量的线性运算:加、减、数乘运算及其运算律
(3)线性运算的应用:直线的方向向量;向量共面
2 类比平面向量的研究方法:
推广
谢
谢
聆
听
