人教A版(2019)必修第一册 5.3.2 函数的极值 课件(21张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 5.3.2 函数的极值 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-15 19:16:48 | ||
图片预览






文档简介
(共21张PPT)
5.3.2 函数的极值与导数
情境导入
题西林壁 苏轼[宋]
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
庐山
群山起伏
庐山
其中蕴含了怎样的数学知识呢?
“横看成岭侧成峰,远近高低各不同”描述的是庐山的高低起伏,错落有致。下图为庐山主峰的部分剖面图:
情景导入
探究新知
F
C
B
E
D
G
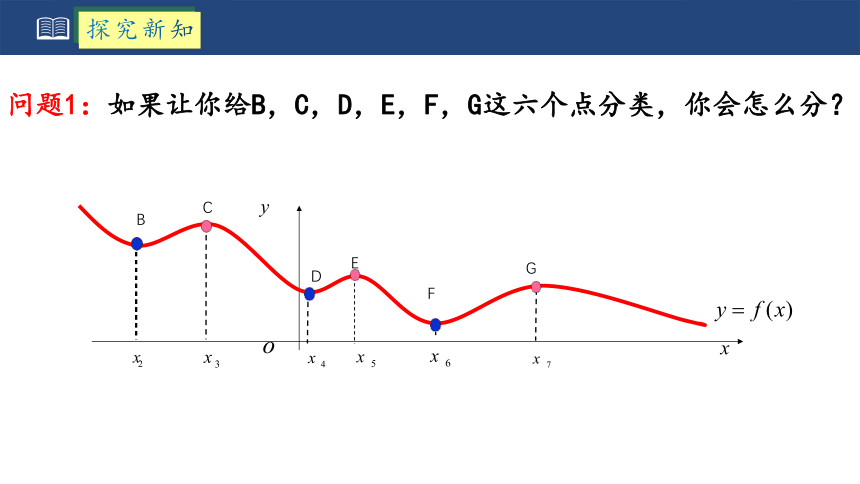
问题1:如果让你给B,C,D,E,F,G这六个点分类,你会怎么分?
探究新知
问题2:观察函数图象,图中的点B处函数值与点B附近的函数值有什么大小关系?
F
C
B
E
D
G
探究新知
F
C
B
E
D
G
问题3:在点B附近 的单调性是怎样变化的 ?
探究新知
F
C
B
E
D
G
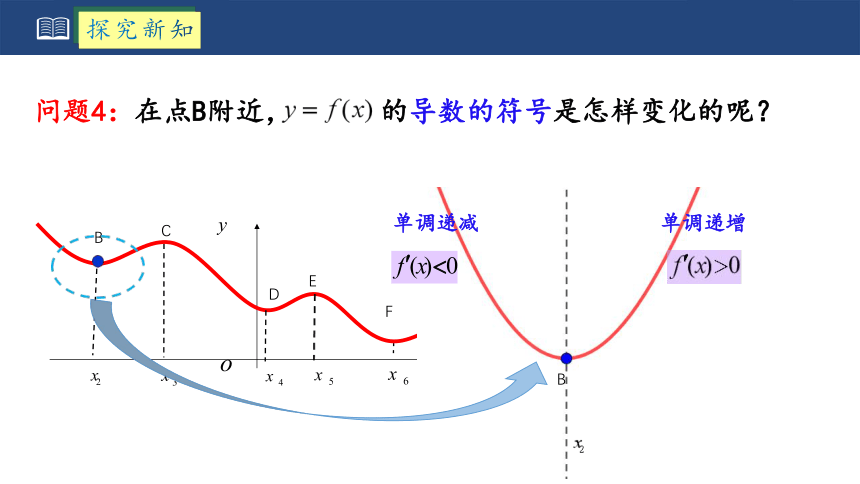
问题4:在点B附近, 的导数的符号是怎样变化的呢?
B
单调递减
单调递增
探究新知
F
C
B
E
D
G
B
单调递减
单调递增
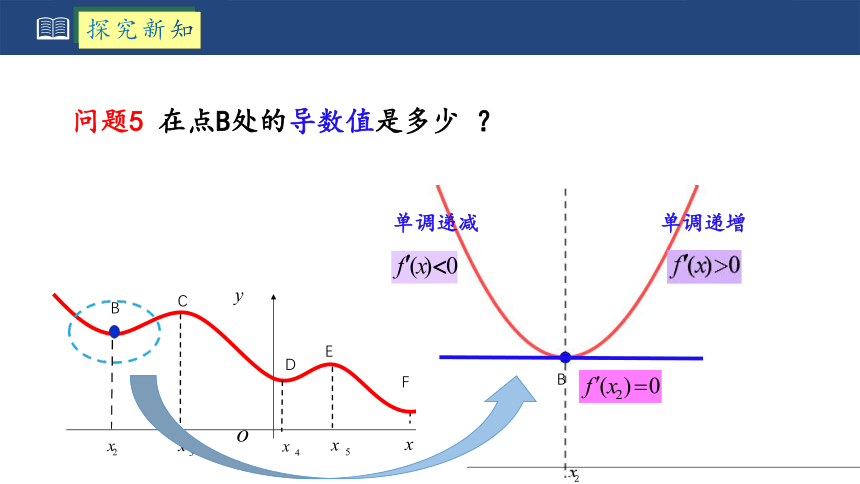
问题5 在点B处的导数值是多少 ?
探究新知
函数值
归纳总结:在点B 处附近
知识海洋
(1)极小值点与极小值
一般地,设函数y=f(x)及y=f'(x)在x=a及其附近有定义,函数y=f(x)在x=a的函数值f(a)比它在x=a附近其他函数值_____,且______;且在x=a的左侧_________,右侧________,则把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
都小
f′(a)=0
f′(x)<0
f′(x)>0
通过类比归纳极大值点与极大值概念?
知识海洋
(2)极大值点与极大值
一般地,设函数y=f(x)及y=f'(x)在x=b及其附近有定义函数y=f(x)在x=b的函数值f(b)比它在x=b附近其他的函数值____,且_______;而且在x=b的左侧________,右侧________,则把b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
f′(x)>0
f′(x)<0
极大值点和极小值点统称为极值点。
极大值和极小值统称为极值。
都大
f′(b)=0
知识海洋
极值点是点吗?
探究新知
问题6:定义在区间[ , ]上的函数 的图象如下, 结合图象回答问题:
(1)极大值点是 ,
极小值是 .
(2)极大值一定大于极小值吗?
(3)函数在其定义域内的极值唯一吗?
极大值与极小值没有必然的大小关系
函数极值不一定唯一
(4)函数在其定义域内的极值点唯一吗?
函数极值点不一定唯一,可以没有,可以有多个,极值点一定在区间
的内部,端点不可能成为极值点
探究新知
问题7:已知函数f(x)=x3,求f ′(0)
对于可导函数f(x):
思考1:0是不是f(x)=x3是的极值点?
对于不导函数f(x)有可能存在极值点,例如
f (x0) =0 x0 是可导函数f (x)的极值点
f (x0)=0 x0是函数f (x)的极值点
思考2:导数为0的根是极值点吗?
合作探究
例1 求函数 的极值.
求f '(x)的零点
列表断号
下结论
定义域
求导函数f '(x)
合作探究
例2 求函数 的极值.
x (0, 1) 1 (1, +∞)
f ′(x) + 0 -
f (x) 单调递增 f (1) 单调递减
你考虑定义域了吗?
你写了无极小值吗?
合作探究
思考:已知函数 在 处取得极值。
求函数 的解析式。
解:
你检验了吗?
合作探究
思考:已知函数 在 处取得极值。
求函数 的解析式。
解:
你能画出它的大致图像吗?
你学会了什么?
尝试总结
尝试总结
看我来记忆
结论:根据导数定函数,两侧互异有极值,
先正后负为极大,先负后正为极小。
“不识庐山真面目,只缘身在此山中”讲的是为什么不能辨别庐山的真面目呢?它其实就是我们下节课要讲的《函数的最值与导数》
谢谢同学们!
5.3.2 函数的极值与导数
情境导入
题西林壁 苏轼[宋]
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
庐山
群山起伏
庐山
其中蕴含了怎样的数学知识呢?
“横看成岭侧成峰,远近高低各不同”描述的是庐山的高低起伏,错落有致。下图为庐山主峰的部分剖面图:
情景导入
探究新知
F
C
B
E
D
G
问题1:如果让你给B,C,D,E,F,G这六个点分类,你会怎么分?
探究新知
问题2:观察函数图象,图中的点B处函数值与点B附近的函数值有什么大小关系?
F
C
B
E
D
G
探究新知
F
C
B
E
D
G
问题3:在点B附近 的单调性是怎样变化的 ?
探究新知
F
C
B
E
D
G
问题4:在点B附近, 的导数的符号是怎样变化的呢?
B
单调递减
单调递增
探究新知
F
C
B
E
D
G
B
单调递减
单调递增
问题5 在点B处的导数值是多少 ?
探究新知
函数值
归纳总结:在点B 处附近
知识海洋
(1)极小值点与极小值
一般地,设函数y=f(x)及y=f'(x)在x=a及其附近有定义,函数y=f(x)在x=a的函数值f(a)比它在x=a附近其他函数值_____,且______;且在x=a的左侧_________,右侧________,则把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
都小
f′(a)=0
f′(x)<0
f′(x)>0
通过类比归纳极大值点与极大值概念?
知识海洋
(2)极大值点与极大值
一般地,设函数y=f(x)及y=f'(x)在x=b及其附近有定义函数y=f(x)在x=b的函数值f(b)比它在x=b附近其他的函数值____,且_______;而且在x=b的左侧________,右侧________,则把b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
f′(x)>0
f′(x)<0
极大值点和极小值点统称为极值点。
极大值和极小值统称为极值。
都大
f′(b)=0
知识海洋
极值点是点吗?
探究新知
问题6:定义在区间[ , ]上的函数 的图象如下, 结合图象回答问题:
(1)极大值点是 ,
极小值是 .
(2)极大值一定大于极小值吗?
(3)函数在其定义域内的极值唯一吗?
极大值与极小值没有必然的大小关系
函数极值不一定唯一
(4)函数在其定义域内的极值点唯一吗?
函数极值点不一定唯一,可以没有,可以有多个,极值点一定在区间
的内部,端点不可能成为极值点
探究新知
问题7:已知函数f(x)=x3,求f ′(0)
对于可导函数f(x):
思考1:0是不是f(x)=x3是的极值点?
对于不导函数f(x)有可能存在极值点,例如
f (x0) =0 x0 是可导函数f (x)的极值点
f (x0)=0 x0是函数f (x)的极值点
思考2:导数为0的根是极值点吗?
合作探究
例1 求函数 的极值.
求f '(x)的零点
列表断号
下结论
定义域
求导函数f '(x)
合作探究
例2 求函数 的极值.
x (0, 1) 1 (1, +∞)
f ′(x) + 0 -
f (x) 单调递增 f (1) 单调递减
你考虑定义域了吗?
你写了无极小值吗?
合作探究
思考:已知函数 在 处取得极值。
求函数 的解析式。
解:
你检验了吗?
合作探究
思考:已知函数 在 处取得极值。
求函数 的解析式。
解:
你能画出它的大致图像吗?
你学会了什么?
尝试总结
尝试总结
看我来记忆
结论:根据导数定函数,两侧互异有极值,
先正后负为极大,先负后正为极小。
“不识庐山真面目,只缘身在此山中”讲的是为什么不能辨别庐山的真面目呢?它其实就是我们下节课要讲的《函数的最值与导数》
谢谢同学们!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
