人教版(2019)必修第二册 5.4 抛体运动的规律 课件(共40张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 5.4 抛体运动的规律 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-15 21:19:12 | ||
图片预览









文档简介
(共40张PPT)
5.4 抛体运动的规律(Ⅰ)
思考:在排球比赛中,如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时速度大小?
课堂引入
平抛运动可分解为
如何处理平抛运动
实验探究
思路:化曲为直
方法:运动的分解
竖直方向的自由落体运动.
水平方向的匀速直线运动.
理论推导
⑵初速度沿水平方向
平抛运动的特征:
⑴只受重力;
竖直方向受力始终为mg,做加速度为g的自由落体运动.
水平方向受力始终为0,做匀速直线运动.
一、平抛运动的速度
v
P
O
x
y
t
θ
vx
vy
v0
如图:一物体以初速度v0水平抛出,不计空气阻力,经过时间t运动到P点,求此时P的速度?
第一步:建立直角坐系标
以抛出点为原点,以初速度v0作为x的方向,竖直方向为y轴方向。
第二步:将速度沿x轴方向和y轴方向分解。
水平方向:匀速直线运动
竖直方向:自由落体运动
速
度
大小:
方向:
θ叫速度偏转角
【例题1】将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
一、平抛运动的速度
竖直方向
即θ = 55°
水平方向
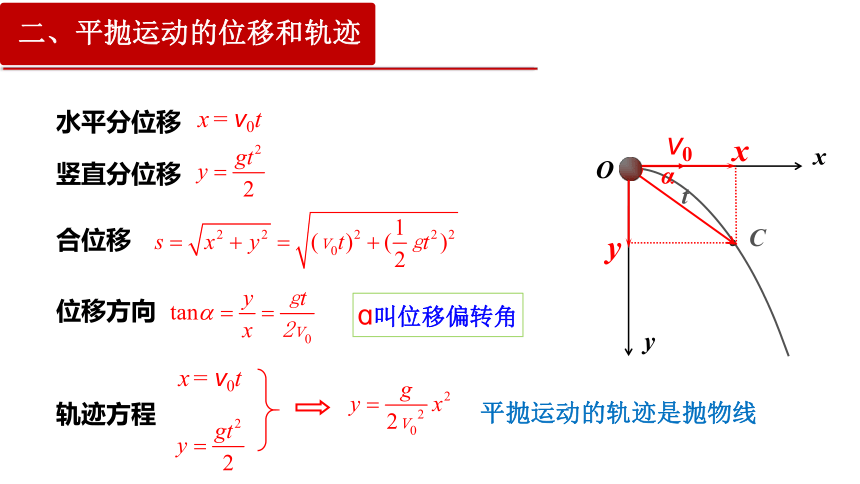
二、平抛运动的位移和轨迹
C
O
x
y
t
v0
x = v0t
位移方向
α
x
y
合位移
水平分位移
竖直分位移
轨迹方程
x = v0t
平抛运动的轨迹是抛物线
ɑ叫位移偏转角
【例题2】 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
二、平抛运动的位移和轨迹
(1)
(2)小球落地点与释放点之间的水平距离
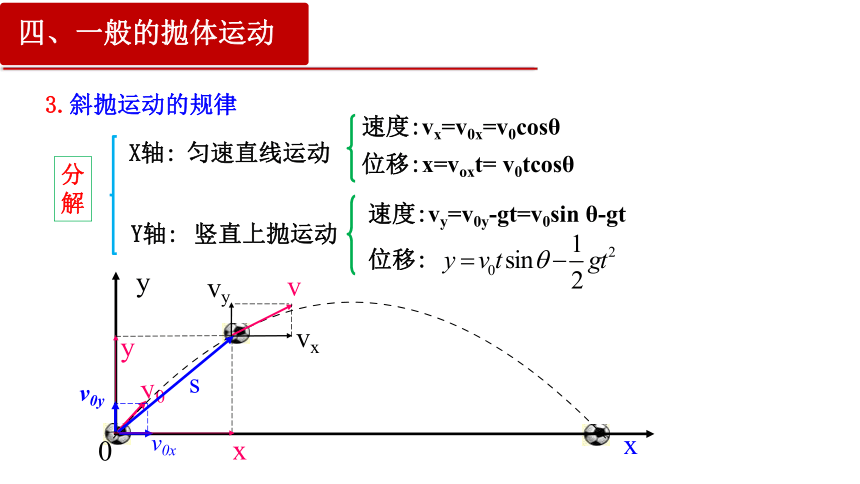
四、一般的抛体运动
1.斜抛运动:
(1)受力特点:在水平方向不受力,加速度为0;
在竖直方向只受重力,加速度为g。
2.斜抛运动的特点
如果物体被抛出时的速度v0是斜向上方或斜向下方,这种抛体运动叫斜抛运动。
(3)对称性特点:①速度对称; ②时间对称; ③轨迹对称
(2)初速度特点:水平方向以vx=v0cosθ 做匀速直线运动;
竖直方向以v0sinθ为初速度做竖直上抛运动。
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X轴:
Y轴:
v0
x
v0x
y
0
v
vx
vy
s
y
x
分
解
3.斜抛运动的规律
四、一般的抛体运动
v0y
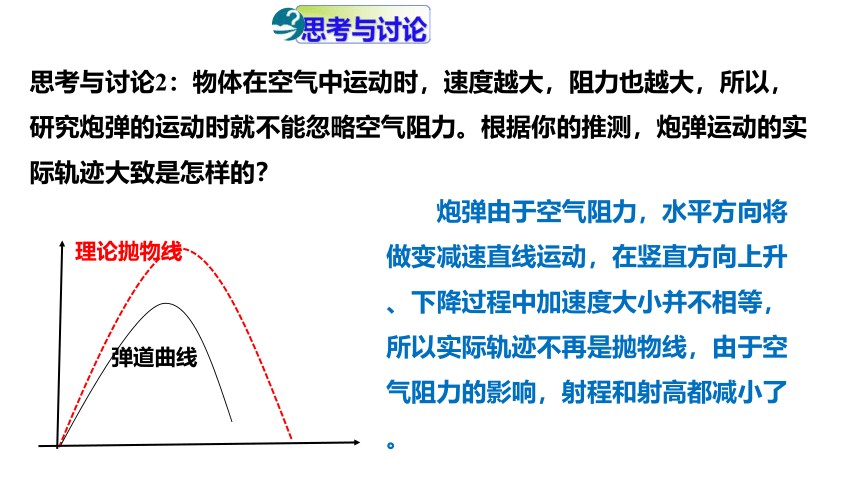
思考与讨论2:物体在空气中运动时,速度越大,阻力也越大,所以,研究炮弹的运动时就不能忽略空气阻力。根据你的推测,炮弹运动的实际轨迹大致是怎样的?
理论抛物线
弹道曲线
炮弹由于空气阻力,水平方向将做变减速直线运动,在竖直方向上升、下降过程中加速度大小并不相等,所以实际轨迹不再是抛物线,由于空气阻力的影响,射程和射高都减小了。
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos
vx=v0cos
vy=v0sin - gt
【典例1】关于平抛运动,下列说法正确的是( )
A.平抛运动是匀速运动
B.平抛运动是匀变速曲线运动
C.平抛运动是非匀变速运动
D.平抛运动的落地速度可能是竖直向下的
典例分析
【正确答案】B
【典例2】斜抛运动与平抛运动相比较,下列说法正确的是( )
A.斜抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
B.都是加速度逐渐增大的曲线运动
C.平抛运动是速度一直增大的运动,而斜抛运动是速度一直减小的运动
D.都是任意两段相等时间内的速度变化量相等的运动
典例分析
【正确答案】D
【典例3】(2021·安徽宣城市·高一期中)质点从同一高度水平抛出,不计空气阻力,下列说法正确的是( )
A.质量越大,水平位移越大
B.质量越小,水平位移越大
C.初速度越大,空中运动时间越长
D.初速度越大,落地速度越大
典例分析
【正确答案】D
【典例4】(2020·合肥百花中学高一期末)如图甲喷出的水做斜抛运动,图乙为水斜抛的轨迹,对轨迹上的两点A、B下列说法正确的是(不计空气阻力)( )
A.A点的速度方向沿切线向上,合力方向竖直向上
B.A点的速度方向沿切线向上,合力方向沿切线向下
C.B点的速度方向沿切线向下,合力方向沿切线向下
D.B点的速度方向沿切线向下,合力方向竖直向下
典例分析
【正确答案】D
【典例5】(2021·北京市怀柔区第二中学高一期中)在水平路面上骑摩托车的人,遇到一个壕沟,其尺寸如图所示。摩托车后轮离开地面后失去动力,可以视为平抛运动。摩托车后轮落到壕沟对面才算安全。(g取10m/s2)。求
(1)摩托车做平抛运动的时间;
(2)摩托车的速度至少要多大才能越过这个壕沟;
(3)摩托车恰好越过壕沟落地时的速度大小。
(结果可保留根号)
典例分析
【正确答案】(1)1s;(2)20m/s;(3)
5.4 抛体运动的规律(Ⅱ)
如图,以抛出点O为坐标原点,以初速度v0方向(水平方向)为x轴方向,竖直向下为y轴方向建立平面直角坐标系。
(2)速度与时间的关系
v0t
gt
平抛运动的基本规律
(1)位移与时间的关系
一、平抛运动的速度变化
速度变化情况
规律:平抛运动任意相等时间 Δt 内的速度变化量相同。
Δv = gΔt
方向恒为竖直向下
B
O
x
y
Δt
v0
v1
A
v2
v3
Δt
C
O
x
y
Δv
v0
v1
v2
v3
Δv
vy1
vy3
vy2
Δv
二、平抛运动的两个推论
v0
x
y
s
vx
v
vy
方向: 位移偏向角
方向 : 速度偏向角
tanθ=2tanα
两个重要的推论
速度的反向延长线交水平位移的中点
【例题1】如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点沿AB以速度v0抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球从抛出到落在半圆环上经历的时间越长;
B.即使v0取值不同,小球落到环上时的速度方向和水平方向的夹角也相同;
C.若v0取值适当,可以使小球垂直撞击半圆环;
D.无论v0取何值,小球都不可能垂直撞击半圆环。
D
三、与斜面有关的平抛运动
运动情形 题干信息 分析方法
从空中水平抛出垂直落到斜面上 速度方向 分解速度,构建速度三角形
vx=v0
vy=gt
θ与v0、t的关系:
三、与斜面有关的平抛运动
从斜面水平抛出又落到斜面上 位移方向 分解位移,构建位移三角形
x=v0t
θ与v0、t的关系:
三、与斜面有关的平抛运动
【例题2】跳台滑雪是一项勇敢者的运动,它需要利用山势特点建造一个特殊跳台.一运动员穿着专用滑雪板,不带雪杖,在滑雪道上获得较高速度后从A点沿水平方向飞出,在空中飞行一段距离后在山坡上B点着陆,如图2所示.已知可视为质点的运动员从A点水平飞出的速度v0=20 m/s,山坡可看成倾角为37°的斜面,不考虑空气阻力(g=10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)运动员在空中的飞行时间t1;
(2)运动员从飞出至落在斜面上的位移大小s;
(3)运动员落到斜面上时的速度大小v;
四、平抛运动的临界问题
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(1)设击球点的高度为2.5 m,问球被水平击出时的速度v0在什么范围内才能使球既不触网也不出界?
五、类平抛运动
【例题4】如图所示的光滑固定斜面长为l、宽为b、倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:(重力加速度为g,不计空气阻力)
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v.
(1)沿斜面向下的方向有mgsinθ=ma,l=at2
联立解得:t=.
解析:
(2)沿水平方向有b=v0t v0==b
(3)物块离开Q点时的速度大小
v===
1、如图,若物体自倾角为θ的固定斜面顶端沿水平方向抛出后仍落在斜面上,则物体与斜面接触时速度与水平方向的夹角φ满足(空气阻力不计,物体可视为质点)( )
A.tan φ=sin θ B.tan φ=cos θ
C.tan φ=tan θ D.tan φ=2tan θ
物体从抛出至落到斜面的过程中,位移方向与水平方向的夹角为θ,落到斜面上时速度方向与水平方向的夹角为φ,由平抛运动的推论知tan φ=2 tan θ,则选项D正确.
D
v0
30°
2、如图所示,以 9.8 m/s 的水平初速度抛出的物体,飞行一段时间后,垂直地撞在倾角 θ = 30°的斜面上,则物体飞行的时间是多少
3.如图所示,水平地面上有一高h=4.2 m的竖直墙,现将一小球以v0=6.0 m/s的速度垂直于墙面水平抛出,已知抛出点与墙面的水平距离s=3.6 m,离地面高H=5.0 m,不计空气阻力,不计墙的厚度.重力加速度g取10 m/s2.
(1)求小球碰墙点离地面的高度h1;
(2)若仍将小球从原位置沿原方向抛出,为使小球能越过竖直墙,
小球抛出时的初速度v的大小应满足什么条件?
O
y
x
vx
vy
L
α
V
θ
图2
两个相对的斜面,倾角分别为37°和53°。在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上。若不计空气阻力,则A、B两个小球的运动时间之比为 ( )
A.1∶1 B.4∶3
C.16∶9 D.9∶16
例1、如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞在倾角为θ=30°的斜面上,则物体的飞行时间为多少?
30°
v
v0
例2、如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,落在斜面上,则物体的飞行时间为多少?
30°
v0
一物体以10m/s的初速度水平抛出,落地时速度与水平方向成45°,求:
(1)落地速度
(2)开始抛出时距地面的高度
(3)水平射程(g=10m/s )
例2.飞机在离地面高度为H的空中,以速度在水平方向上匀速飞行,每隔相等时间间隔从飞机上放下一只球,不计空气阻力,下列说法中正确的是( )
A.小球在空中排成竖直线,它们的落地点是等间距的
B.小球在空中排成竖直线,它们的落地点是不等间距的
C.小球在空中排成抛物线,它们的落地点是等间距的
D.小球在空中排成抛物线,它们的落地点是不等间距的
如图为一小球作平抛运动的频闪照片的一部分。图中背景方格的边长均为5cm。如果g取10m/s2,求:
(1)则闪光的时间间隔是多少?
(2)平抛初速度是多少?
(4)求出抛出点O的坐标
(3)求B点的竖直分速度
如图所示,水平屋顶高H=5 m,围墙高h=3.2 m,围墙到房子的水平距离L=3 m,围墙外马路宽x=10 m,为使小球从屋顶水平飞出落在围墙外的马路上,求小球离开屋顶时的速度v的大小范围.(g取10 m/s2)
5.4 抛体运动的规律(Ⅰ)
思考:在排球比赛中,如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时速度大小?
课堂引入
平抛运动可分解为
如何处理平抛运动
实验探究
思路:化曲为直
方法:运动的分解
竖直方向的自由落体运动.
水平方向的匀速直线运动.
理论推导
⑵初速度沿水平方向
平抛运动的特征:
⑴只受重力;
竖直方向受力始终为mg,做加速度为g的自由落体运动.
水平方向受力始终为0,做匀速直线运动.
一、平抛运动的速度
v
P
O
x
y
t
θ
vx
vy
v0
如图:一物体以初速度v0水平抛出,不计空气阻力,经过时间t运动到P点,求此时P的速度?
第一步:建立直角坐系标
以抛出点为原点,以初速度v0作为x的方向,竖直方向为y轴方向。
第二步:将速度沿x轴方向和y轴方向分解。
水平方向:匀速直线运动
竖直方向:自由落体运动
速
度
大小:
方向:
θ叫速度偏转角
【例题1】将一个物体以10 m/s的速度从10 m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10 m/s2。
一、平抛运动的速度
竖直方向
即θ = 55°
水平方向
二、平抛运动的位移和轨迹
C
O
x
y
t
v0
x = v0t
位移方向
α
x
y
合位移
水平分位移
竖直分位移
轨迹方程
x = v0t
平抛运动的轨迹是抛物线
ɑ叫位移偏转角
【例题2】 如图,某同学利用无人机玩“投弹”游戏。无 人机以 v0 = 2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h = 20 m,空气阻力忽略不计,g 取 10 m/s2 。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
二、平抛运动的位移和轨迹
(1)
(2)小球落地点与释放点之间的水平距离
四、一般的抛体运动
1.斜抛运动:
(1)受力特点:在水平方向不受力,加速度为0;
在竖直方向只受重力,加速度为g。
2.斜抛运动的特点
如果物体被抛出时的速度v0是斜向上方或斜向下方,这种抛体运动叫斜抛运动。
(3)对称性特点:①速度对称; ②时间对称; ③轨迹对称
(2)初速度特点:水平方向以vx=v0cosθ 做匀速直线运动;
竖直方向以v0sinθ为初速度做竖直上抛运动。
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X轴:
Y轴:
v0
x
v0x
y
0
v
vx
vy
s
y
x
分
解
3.斜抛运动的规律
四、一般的抛体运动
v0y
思考与讨论2:物体在空气中运动时,速度越大,阻力也越大,所以,研究炮弹的运动时就不能忽略空气阻力。根据你的推测,炮弹运动的实际轨迹大致是怎样的?
理论抛物线
弹道曲线
炮弹由于空气阻力,水平方向将做变减速直线运动,在竖直方向上升、下降过程中加速度大小并不相等,所以实际轨迹不再是抛物线,由于空气阻力的影响,射程和射高都减小了。
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos
vx=v0cos
vy=v0sin - gt
【典例1】关于平抛运动,下列说法正确的是( )
A.平抛运动是匀速运动
B.平抛运动是匀变速曲线运动
C.平抛运动是非匀变速运动
D.平抛运动的落地速度可能是竖直向下的
典例分析
【正确答案】B
【典例2】斜抛运动与平抛运动相比较,下列说法正确的是( )
A.斜抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动
B.都是加速度逐渐增大的曲线运动
C.平抛运动是速度一直增大的运动,而斜抛运动是速度一直减小的运动
D.都是任意两段相等时间内的速度变化量相等的运动
典例分析
【正确答案】D
【典例3】(2021·安徽宣城市·高一期中)质点从同一高度水平抛出,不计空气阻力,下列说法正确的是( )
A.质量越大,水平位移越大
B.质量越小,水平位移越大
C.初速度越大,空中运动时间越长
D.初速度越大,落地速度越大
典例分析
【正确答案】D
【典例4】(2020·合肥百花中学高一期末)如图甲喷出的水做斜抛运动,图乙为水斜抛的轨迹,对轨迹上的两点A、B下列说法正确的是(不计空气阻力)( )
A.A点的速度方向沿切线向上,合力方向竖直向上
B.A点的速度方向沿切线向上,合力方向沿切线向下
C.B点的速度方向沿切线向下,合力方向沿切线向下
D.B点的速度方向沿切线向下,合力方向竖直向下
典例分析
【正确答案】D
【典例5】(2021·北京市怀柔区第二中学高一期中)在水平路面上骑摩托车的人,遇到一个壕沟,其尺寸如图所示。摩托车后轮离开地面后失去动力,可以视为平抛运动。摩托车后轮落到壕沟对面才算安全。(g取10m/s2)。求
(1)摩托车做平抛运动的时间;
(2)摩托车的速度至少要多大才能越过这个壕沟;
(3)摩托车恰好越过壕沟落地时的速度大小。
(结果可保留根号)
典例分析
【正确答案】(1)1s;(2)20m/s;(3)
5.4 抛体运动的规律(Ⅱ)
如图,以抛出点O为坐标原点,以初速度v0方向(水平方向)为x轴方向,竖直向下为y轴方向建立平面直角坐标系。
(2)速度与时间的关系
v0t
gt
平抛运动的基本规律
(1)位移与时间的关系
一、平抛运动的速度变化
速度变化情况
规律:平抛运动任意相等时间 Δt 内的速度变化量相同。
Δv = gΔt
方向恒为竖直向下
B
O
x
y
Δt
v0
v1
A
v2
v3
Δt
C
O
x
y
Δv
v0
v1
v2
v3
Δv
vy1
vy3
vy2
Δv
二、平抛运动的两个推论
v0
x
y
s
vx
v
vy
方向: 位移偏向角
方向 : 速度偏向角
tanθ=2tanα
两个重要的推论
速度的反向延长线交水平位移的中点
【例题1】如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点沿AB以速度v0抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球从抛出到落在半圆环上经历的时间越长;
B.即使v0取值不同,小球落到环上时的速度方向和水平方向的夹角也相同;
C.若v0取值适当,可以使小球垂直撞击半圆环;
D.无论v0取何值,小球都不可能垂直撞击半圆环。
D
三、与斜面有关的平抛运动
运动情形 题干信息 分析方法
从空中水平抛出垂直落到斜面上 速度方向 分解速度,构建速度三角形
vx=v0
vy=gt
θ与v0、t的关系:
三、与斜面有关的平抛运动
从斜面水平抛出又落到斜面上 位移方向 分解位移,构建位移三角形
x=v0t
θ与v0、t的关系:
三、与斜面有关的平抛运动
【例题2】跳台滑雪是一项勇敢者的运动,它需要利用山势特点建造一个特殊跳台.一运动员穿着专用滑雪板,不带雪杖,在滑雪道上获得较高速度后从A点沿水平方向飞出,在空中飞行一段距离后在山坡上B点着陆,如图2所示.已知可视为质点的运动员从A点水平飞出的速度v0=20 m/s,山坡可看成倾角为37°的斜面,不考虑空气阻力(g=10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
(1)运动员在空中的飞行时间t1;
(2)运动员从飞出至落在斜面上的位移大小s;
(3)运动员落到斜面上时的速度大小v;
四、平抛运动的临界问题
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(1)设击球点的高度为2.5 m,问球被水平击出时的速度v0在什么范围内才能使球既不触网也不出界?
五、类平抛运动
【例题4】如图所示的光滑固定斜面长为l、宽为b、倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:(重力加速度为g,不计空气阻力)
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v.
(1)沿斜面向下的方向有mgsinθ=ma,l=at2
联立解得:t=.
解析:
(2)沿水平方向有b=v0t v0==b
(3)物块离开Q点时的速度大小
v===
1、如图,若物体自倾角为θ的固定斜面顶端沿水平方向抛出后仍落在斜面上,则物体与斜面接触时速度与水平方向的夹角φ满足(空气阻力不计,物体可视为质点)( )
A.tan φ=sin θ B.tan φ=cos θ
C.tan φ=tan θ D.tan φ=2tan θ
物体从抛出至落到斜面的过程中,位移方向与水平方向的夹角为θ,落到斜面上时速度方向与水平方向的夹角为φ,由平抛运动的推论知tan φ=2 tan θ,则选项D正确.
D
v0
30°
2、如图所示,以 9.8 m/s 的水平初速度抛出的物体,飞行一段时间后,垂直地撞在倾角 θ = 30°的斜面上,则物体飞行的时间是多少
3.如图所示,水平地面上有一高h=4.2 m的竖直墙,现将一小球以v0=6.0 m/s的速度垂直于墙面水平抛出,已知抛出点与墙面的水平距离s=3.6 m,离地面高H=5.0 m,不计空气阻力,不计墙的厚度.重力加速度g取10 m/s2.
(1)求小球碰墙点离地面的高度h1;
(2)若仍将小球从原位置沿原方向抛出,为使小球能越过竖直墙,
小球抛出时的初速度v的大小应满足什么条件?
O
y
x
vx
vy
L
α
V
θ
图2
两个相对的斜面,倾角分别为37°和53°。在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上。若不计空气阻力,则A、B两个小球的运动时间之比为 ( )
A.1∶1 B.4∶3
C.16∶9 D.9∶16
例1、如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞在倾角为θ=30°的斜面上,则物体的飞行时间为多少?
30°
v
v0
例2、如图,以10m/s的水平初速度抛出的物体,飞行一段时间后,落在斜面上,则物体的飞行时间为多少?
30°
v0
一物体以10m/s的初速度水平抛出,落地时速度与水平方向成45°,求:
(1)落地速度
(2)开始抛出时距地面的高度
(3)水平射程(g=10m/s )
例2.飞机在离地面高度为H的空中,以速度在水平方向上匀速飞行,每隔相等时间间隔从飞机上放下一只球,不计空气阻力,下列说法中正确的是( )
A.小球在空中排成竖直线,它们的落地点是等间距的
B.小球在空中排成竖直线,它们的落地点是不等间距的
C.小球在空中排成抛物线,它们的落地点是等间距的
D.小球在空中排成抛物线,它们的落地点是不等间距的
如图为一小球作平抛运动的频闪照片的一部分。图中背景方格的边长均为5cm。如果g取10m/s2,求:
(1)则闪光的时间间隔是多少?
(2)平抛初速度是多少?
(4)求出抛出点O的坐标
(3)求B点的竖直分速度
如图所示,水平屋顶高H=5 m,围墙高h=3.2 m,围墙到房子的水平距离L=3 m,围墙外马路宽x=10 m,为使小球从屋顶水平飞出落在围墙外的马路上,求小球离开屋顶时的速度v的大小范围.(g取10 m/s2)
