高一苏教版必修3统计部分[下学期]

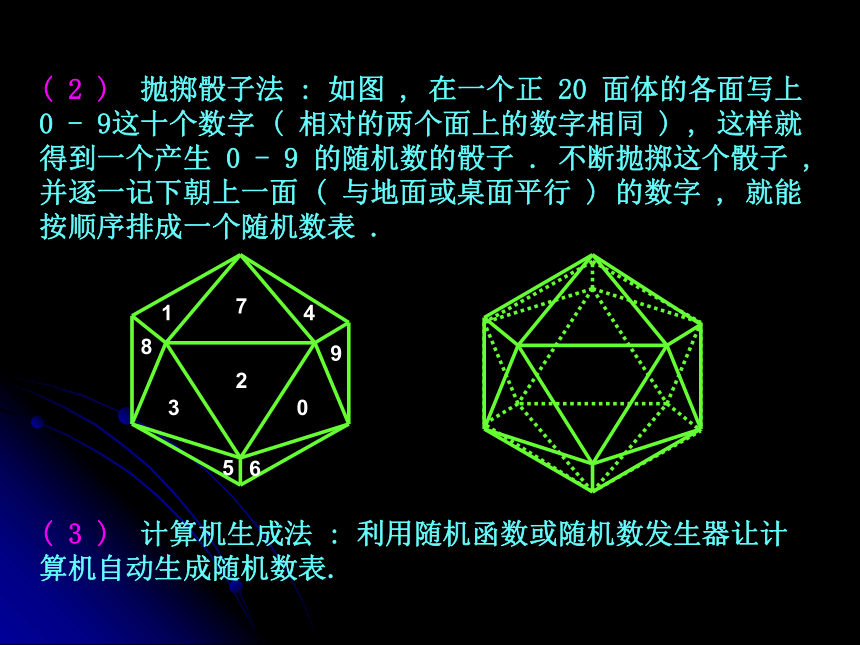
课件76张PPT。第六章 统 计 6.1 抽 样 方 法 6.1.1 简单随机抽样 1. 抽签法 为了了解高二某班 50 名学生的视力状况 , 从中抽取 10 名学生进行检查 . 如何抽取呢 ? 通常使用抽签法,方法是: 将 50 名学生从 1 到 50 进行编号 , 再制作 1 到 50 的 50 个号签 , 把 50 个号签集中在一起并充分搅匀 , 最后随机地从中抽 10 个号签 . 对编号与抽中的号签的号码相一致的学生进行视力检查 . 一般地 , 用抽签法从个体个数为 N 的总体中抽取一个容量为 k 的样本的步骤为 :( 1 ) 将总体中的所有个体编号 ( 号码可以从 1 到 N ) ;( 2 ) 将 1 到 N 这 N 个号码写在形状 、大小相同的号签上 ( 号签可以用小球 、卡片 、纸条等制作 ) ;( 3 ) 将号签放在同一箱中,并搅拌均匀 ;( 4 ) 从箱中每次抽取一个号签 , 并记录其编号 , 连续抽取 k 次 ;( 5 ) 从总体中将与抽到的签的编号相一致的个体取出. 抽签法简单易行 , 适用于总体中个体数不多的情形 .2. 随机数表法 用抽签法抽取样本时 , 编号的过程有时可以省略 ( 如用已有的编号 ) , 但制签的过程就难以省去了 , 而且制签也比较麻烦 . 如何简化制签的过程呢 ? 一个有效的办法是制作一个表 , 其中的每个数都是用随机方法产生的 , 这样的表称为随机数表 . 于是 , 我们只要按一定的规则到随机数表中选取号码就可以了 . 这种抽样方法叫做随机数表法 . 随 机 数 表 的 制 作 随机数表是人们根据需要编制出来的 , 由0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 十个数字组成 , 表中每一个数字都是用随机方法产生的 ( 称为 " 随机数 " ) . 随机数的产生方法主要有抽签法 、 抛掷骰子法和计算机生成法 .( 1 ) 抽签法 : 用 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 十个数字做十个签 , 放入一个箱中并搅拌均匀 , 再从箱中每次抽出一个签并记下签的数码 , 再放回箱中 , 如此重复进行下去即可得到一个随机数表 . 若要三位数表 , 就三三连在一起 , 如 012 , 321 , 249 , 460 , 634 , 105 , · · · . 如果需要两位数表 , 则将所得的各个数码按顺序两两连在一起 . 如 01 , 07 , 15 , 34 , 76 , 93 , · · · .( 2 ) 抛掷骰子法 : 如图 , 在一个正 20 面体的各面写上 0 - 9这十个数字 ( 相对的两个面上的数字相同 ) , 这样就得到一个产生 0 - 9 的随机数的骰子 . 不断抛掷这个骰子 , 并逐一记下朝上一面 ( 与地面或桌面平行 ) 的数字 , 就能按顺序排成一个随机数表 . 1234567890( 3 ) 计算机生成法 : 利用随机函数或随机数发生器让计算机自动生成随机数表.下面我们用随机数表法求解本节开头的问题.( 1 ) 对 50 名学生进行编号 , 编号分别为 01 , 02 , 03 , ··· , 50 ;( 2 ) 在随机数表中随机地确定一个数作为开始 , 如第 8 行第 29列的数 7 开始 . 为了便于说明 , 我们将附表中的第 6 行至第 10行摘录如下 : 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 6484 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 1 9 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5457 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28( 3 ) 从数7开始向右读下去 , 每次读两位 , 凡不在 01 到 50 中的数跳过去不读 , 遇到已经读过的数也跳过去 , 便可依次得到12 , 07 , 44 , 39 , 38 , 33 , 21 , 34 , 29 , 42这 10 个号码 , 就是所要抽取的 10 个样本个体的号码 . 当随机地选定开始的数后 , 读数的方向可以向左 , 也可以向右、向上、向下等.由此可见,用随机数表法抽取样本的步骤是:( 1 ) 对总体中的个体进行编号 ( 每个号码位数一致 ) ;( 2 ) 在随机数表中任选一个数作为开始 ;( 3 ) 从选定的数开始按一定的方向读下去 , 得到的数码若不在编号中 , 则跳过;若在编号中 , 则取出 ; 如果得到的号码前面已经取出 , 也跳过;如此继续下去 , 直到取满为止 ;( 4 ) 根据选定的号码抽取样本 . 从个体数为N的总体中不重复地取出 n 个个体 ( n ? N ) ,每个个体都有相同的机会被取到 . 这样的抽样方法称为简单随机抽样 .抽签法和随机数表法都是简单随机抽样 .练习1. 一个学生在一次知识竞赛中要回答的 8 道题是这样产生的 : 从 15 道历史题中随机抽出 3 道 , 从 20 道地理题中随机抽出 3 道 , 从 12 道生物题中随机抽出 2 道 . 试用抽签法确定这个学生所要回答的三门学科的题的序号 ( 历史题编号分别为 1 , 2 , · · · , 15 , 地理体编号分别为 16 , 17 , · · · , 35 , 生物题编号分别为 36 , 37 , · · · , 47 ) .从 01 , 02 , 03 , 04 , 05 , 06 , 07 , 08 , 09 , 10 , 11 , 12 , 13 , 14 , 15 中随机抽出 3 道 ;从 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 中随机抽出 3 道 ;从 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44 , 45 , 46 , 47 中随机抽出 2 道 .练习2. 从 100 件电子产品中抽取一个容量为 25 的样本进行检测 , 试用随机数表法抽取样本 .16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 6484 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5457 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28练习3. 假设一个总体有 5 个元素 , 分别记为 a , b , c , d , e , 从中采用不重复抽取样本的方法 , 抽取一个容量为 2 的样本,样本共有多少个 ? 写出全部可能的样本 .样本共有 10 种 ,可能的样本是 :a , b ; a , c ; a , d ; a , e ; b , c ; b , d ; b , e ; c , d ; c , e ; d , e .练习4. 某学校高一年级共有 200 名学生 , 为了了解这些学生的身高状况 , 从中抽取一个容量为 15 的样本 .012 234 409 987 001 333 761 078 142 765 020 769 999 456 1 32 001 667 089 034072 134 407 207 051 146 657 456 001 149 876 01 0 639 9 1 1 1 17 169 1 1 9 1 1 0 667 请同学们自己试一试6.1.2 系统抽样 某校高一年级共有 2 0 个班 , 每班有 5 0 名学生 . 为了了解高一学生的视力状况 , 从这 1 0 0 0 人中抽取一个容量为 1 0 0 的样本进行检查 , 应该怎样抽样 ? 通常先将各班平均分成 5 组 , 再在第一组 ( 1 到 10 号学生 ) 中用抽签法抽取一个 , 然后按照 “ 逐次加 10 ( 每组中个体个数 ) ” 的规则分别确定学号为 11 到 20 、21 到 30 、31 到 40 、41 到 50 的学生代表 . 将总体平均分成几个部分 , 然后按照预先定出的规则 , 从每个部分中抽取一个个体 , 得到所需的样本 , 这样的抽样方法称为 系统抽样 . 系统抽样的步骤为: ( 1 ) 采用随机的方式将总体中的个体编号 ;( 2 ) 将整个的编号按一定的间隔 ( 设 为 k ) 分段 , 当 N / n ( N 为总体中的个体数 , n 为样本容量 ) 是整数时 , k = N / n ; 当 N / n 不是整数时 , 从总体中剔除一些个体 , 使剩下的总体中个体的个数 N ’ 能被 n 整除 , 这时 k= N ’ / n , 并将剩下的总体重新编号 ;( 3 ) 在第一段中用简单随机抽样确定起始的个体编号 l ;( 4 ) 将编号为 l , l + k , l + 2 k , · · · , l + ( n – 1 ) k 的个体抽出 .例1. 某单位在岗职工共 624人 , 为了调查工人用于上班途中的时间 , 决定抽取 10 % 的工人进行调查 . 如何采用系统抽样方法完成这一抽样 ?分析 : 因为 624 的 10 % 约为 62 , 624 不能被 62 整除 , 为了保证 “ 等距 ” 分段 , 应先剔除 4 人 .解:第一步 将 624 名职工用随机方式进行编号 ;第二步 从总体中剔除 4 人 ( 剔除方法可用随机数表法 ) ,将剩下的 620 名职工重新编号 ( 分别为000 , 001 ,002 , · · · , 619 ) , 并分为 62 段 ;第三步 在第一段 000 , 001 , 002 , · · · , 009 这十个编号中用简单随机抽样确定起始号码 i 0 ;第四步 将编号为 i 0 , i 0 + 10 , i 0 + 20 , · · · , i 0 + 610 的个体抽出,组成样本 .练习1 . 为了了解参加一次知识竞赛的 1252 名学生的成绩 , 决定采用系统抽样的方法抽取一个容量为 50 的样本 , 那么总体中应随机剔除个体的数目是 ( )A . 2B . 3C . 4D . 5A 练习2 . 要从 1003 名学生中选取一个容量为 20 的样本 , 试叙述系统抽样的步骤 .解 :第一步 将 1003 名学生用随机方式编号为 0000 , 0001 , 0002 , · · · , 1002 ;第二步 从总体中剔除 3 个个体 ( 剔除方法可用随机数表法) ;第三步 将剩下的 1000 名学生重新编号 ( 分别为000 , 001 , 002 , · · · , 999 号 ) , 并平均分成 20 段 ;第四步 在第一段 000 , 001 , 002 , · · · , 049 这 50 个编号中随机地抽取一个号码 ( 可用抽签法或随机数表法 ) i 0 , 则编号为 i 0 + 50 , i 0 + 100 , i 0 + 150 , · · · , i 0 + 950 的个体就可组成抽取的样本 .练习3 . 试用系统抽样的方法从你校学生中抽取适当的样本 , 再对抽出的学生的两臂平展的长度及身高进行测量 , 分别计算两组数据的平均数 .6.1.3 分层抽样 某校高一 、高二和高三年级分别有学生 1000 , 800 和 700 名 , 为了了解全校学生的视力情况,欲从中抽取容量为 100 的样本 , 怎样抽取较为合理 ? 一个有效的方法是 : 使选取的样本中各年级学生所占的比与实际人数占总体人数的比基本相同 . 一般地 , 当总体由差异明显的几个部分组成时 , 为了使样本更客观地反映总体情况 , 我们常常将总体中的个体按不同的特点分成层次比较分明的几部分 , 然后按各部分在总体中所占的比实施抽样 , 这种抽样方法叫分层抽样 . 分层抽样的步骤为: ( 1 ) 将总体按一定标准分层 ;( 2 ) 计算各层的个体数与总体的个体数的比 ;( 3 ) 按各层个体数占总体的个体数的比确定各层应抽取的样本容量 ;( 4 ) 在每一层进行抽样 ( 可用简单随机抽样或系统抽样 ) .例 2 . 某电视台在因特网上就观众对某一节目的喜爱程度进行调查 , 参加调查的总人数为 12000 人 , 其中持各种态度的人数如下表所示 : 电视台为了进一步了解观众的具体想法和意见 , 打算从中抽取 60 人进行更为详细的调查 , 应怎样进行抽样 ?解 :可用分层抽样的方法 , 其总体容量为 12000 . 因此 , 采用分层抽样的方法在 “ 很喜爱 ” 、“ 喜爱 ” 、 “ 一般 ” 和 “ 不喜爱 ” 的 2435 人 、4567 人 、3926 人 和 1072 人中分别抽取 12人 、23 人 、20 人 和 5 人 .练习1. 在某年有奖明信片销售活动中 , 规定每 100 万张为一个开奖组 , 通过随机抽取的方式确定号码的后四位数为 2709 的为三等奖 . 这样确定获奖号码的抽样方法是系 统 抽 样 .练习2. 某公司生产三种型号的轿车 , 产量分别为 1200 辆 、6000 辆和 2000 辆 . 为检验该公司的产品质量 , 现用分层抽样的方法抽取 46 辆进行检验 , 这三种型号的轿车应分别抽取解: 其总体容量为 9200 辆 .6辆 、30 辆 和 10 辆 .练习3. 某所学校有小学部 、初中部和高中部 , 在校小学生 、初中生和高中生之比为 5 : 2 : 3 , 且已知初中生有 800 人 . 现要从这所学校中抽取一个容量为 80 的样本以了解他们对某一问题的看法 , 应采用什么抽样方法 ? 从小学部 、初中部及高中部各抽取多少名 ? 总体上看 , 平均多少名学生中抽取到一名学生 ?解 :可用分层抽样的方法 , 由条件可知小学部有 2000 人 , 高中部有1200 人 , 其总体容量为 4000 人 .因为 40 + 16 + 24 = 80 , 所以平均 50 名学生中抽取一名学生.练习4. 将你所在班级的同学按性别分成两个组分别编号 , 制成号签 , 分别放在两个箱子里搅拌均匀 , 然后按男女生之比各抽出若干个号签 , 组成两个样本 , 就他们对某一方面问题的看法进行调查 , 以比较男女同学对该问题看法上的差异 . 请同学们自己试一试 以上我们学习了三种抽样方法 , 这些抽样方法的特点及适用范围可归纳如下 :简单随机抽样系统抽样分层抽样从总体中逐个抽取 将总体平均分成几部分 , 按事先确定的规则分别在各部分中抽取 将总体分成几层 , 按各层个体数之比抽取 在起始部分抽样时 , 采用简单随机抽样 各层抽样时采用简单随机抽样或系统抽样 总体中的个体个数较少 总体中的个体个数较多 总体由差异明显的几个部分组成 抽样过程中每个个体被抽到的可能性相同例 3 . 下列问题中 , 采用怎样的抽样方法较为合理 ?( 1 ) 从 10 台冰箱中抽取 3 台进行质量检查 ;( 2 ) 某电影院有 32 排座位 , 每排有 40 个座位 , 座位号为1 ~ 40 . 有一次报告会坐满了听众 , 报告会结束以后为听取意见 , 需留下 32 名听众进行座谈 ; ( 3 ) 某学校有 160 名教职工 , 其中教师 120 名 , 行政人员16 名 , 后勤人员 24 名 . 为了了解教职工对学校在校务公开方面的意见 , 拟抽取一个容量为 20 的样本 .解 :( 1 ) 总体容量比较小 , 用抽签法或随机数表法 .( 2 ) 总体容量比较大 , 人员没有明显差异 , 且刚好 32 排 ,每排人数相同 , 可采用系统抽样 . 将每排的 40 个人组成一组 , 共 32 组 , 从第一排至第 32 排分别为第 1 ~ 32 组 , 先在第一排用简单随机抽样法抽出一名听众 , 再将其他各排与此听众座位号相同的听众全部取出 . ( 3 ) 差异明显 , 采用分层抽样 . 总体容量为 160 , 故样本中教师人数应为 20 × ( 120 / 160 ) = 15 名 , 行政人员应为 20 × ( 16 / 160 ) = 2 名 , 后勤人员应为 20 × ( 24 / 160 ) = 3名.练习1. 某商场想通过检查发票及销售记录的 2 % 来快速估计每月的销售总额 , 采取如下方法 : 从某本 50 张的发票存根中随机抽取一张 , 如 15 号 , 然后按顺序往后将 65 号 、115 号 、165 号发票上的销售额组成一个调查样本 . 这种抽取样本的方法是 ( )A . 抽签法B . 系统抽样C . 分层抽样D . 随机数表法B 练习2. 某科研机构由行政人员 、科技人员和后勤职工三种不同类型的人员组成 , 现要抽取一个容量为 45 的样本进行调查 . 已知科技人员共有 60 人 , 抽入样本的有 20 人 , 且行政人员与后勤职工人数之比为 2 : 3 , 则此机构的总人数 、行政人员 、后勤职工人数分别为多少 ?解:可用分层抽样的方法 , 由条件设总人数为 x 人 , 行政人员 y 人 , 后勤人员 z 人 .得 x = 135 人 .又 135 = 60 + y + z , 且 y : z = 2 : 3 .得 y = 30 人 , z = 45 人 . 答 : 总人数为 135 人 , 行政人员 30 人 , 后勤职工 45 人 .练习3. 一个单位有职工 160 人 , 其中业务人员 96 人 , 管理人员 40 人 , 后勤人员 24 人 . 为了了解职工的某种情况 , 要从中抽取一个容量为 20 的样本 , 按下述三种方法抽取 :( 1 ) 将 160 人从 1 至 160 编号 , 用白纸做成有 1 至 160 号的签放入箱内搅匀 , 然后从中抽取 20 个签 , 与签号相同的 20 个人被选出 .( 2 ) 将 160 人从 1 至 160 编号 , 按编号顺序分成 20 组 , 每组 8 人 , 号码分别为 1 ~ 8 号 、 9 ~ 16 号 、 · · · 、 153 ~ 160 号 , 先从第 1 组中用抽签法抽出 k ( 0 ? k ? 9 ) 号 , 其余组的 ( k + 8 n ) 号( n = 1 , 2 , · · · , 19 ) 亦被抽到 , 如此抽到 20 人 ;( 3 ) 按 20 : 160 = 1 : 8 的比例 , 从业务人员中抽取 12 人 , 从管理人员中抽取 5 人 , 从后勤人员中抽取 3 人 , 都用随机数表法从各类人员中抽取所需的人数 , 他们合在一起恰好抽到 20 人 .上述三种方法中,按简单随机抽样 、分层抽样 、系统抽样的顺序是 ( )A . ( 1 ) ( 2 ) ( 3 )B . ( 2 ) ( 1 ) ( 3 )C . ( 1 ) ( 3 ) ( 2 )D . ( 3 ) ( 1 ) ( 2 )C 习 题 6.11 . 为了了解某市 800 家企业的管理情况 , 拟抽取 40 家企业作为样本 . 这 800 家企业中有中外合资企业 160 家 , 私营企业 320 家 , 国有企业 240 家 , 其他性质的企业 80 家 . 如何抽取较合理 ?解 :用分层抽样法较合理 , 总容量为 800 .2 . 用分层抽样法从某学校学生中抽取一个容量为 45 的样本 , 其中高一年级抽 20 人 , 高三年级抽 10 人 . 已知该校高二年级共有学生 300 人 , 求该校学生总数 .解 :可用分层抽样的方法 , 设总人数为 x 人 .由题意知高二年级需抽取 15 人 .得总人数为 900 人 .3 . 某市的 4 个区共有 20000 名学生 , 且 4 个区的学生人数之比为 3 : 2 . 8 : 2 . 2 : 2 . 现要用分层抽样的方法从所有学生中抽取一个容量为 200 的样本 , 那么在这 4 个区中分别应抽取多少名学生 ?解 :设 4 个区的学生人数分别为 x , y , z , w .答 : 4 个区的学生人数分别为 60 人 , 56 人 , 44 人 , 40 人 .8 . 某校高一年级 500 名学生中 , 血型为 O 型的有 200 人 , A 型的有 125 人 , B 型的有 125 人 , AB 型的有 50 人 . 为了研究血型与色弱之间的关系 , 要从中抽取一个容量为 40 的样本 , 应如何抽取 ? 写出 AB 型的样本的抽样过程 .解 :第一步, 将 AB 型的 50 人进行编号 , 分别为 00 , 01 , 02 , ···, 49 ;第二步, 将 00 , ···, 49 这 50 个号码写在形状 、大小相同的号签上 ; 第三步, 将号签放在一个箱子中,并搅拌均匀;第四步, 从箱中每次抽取一个号签 , 连续抽取 4 次 ;第五步, 将 AB 型的 50 人中与号签编码相同的人取出 .6.2 总体分布的估计 为了了解 7 月 25 日至 8 月 24 日北京地区的气温分布情况 , 我们对以往年份这段时间的日最高气温进行抽样 , 并对得到的数据进行分析 . 我们随机抽取近年来北京地区 7 月 25 日 至 8 月 24 日的日最高气温 , 得到如下样本 ( 单位 : 0 C ) :41 . 937 . 535 . 735 . 437 . 238 . 134 . 733 . 733 . 332 . 534 . 633 . 030 . 831 . 028 . 631 . 528 . 828 . 631 . 528 . 833 . 232 . 530 . 330 . 229 . 833 . 132 . 829 . 425 . 624 . 730 . 030 . 129 . 530 . 3怎样通过上表的数据 , 分析比较两时间段的高温 ( ≥ 33 0 C )状况呢 ?6.2.1 频率分布表 33 . 333 . 1上面两个样本中的高温天数的频率用下表表示 :时 间总 天 数1717高 温 天 数( 频 数 )112 频 率0.6470.118 由此表可以发现近年来北京地区 7 月25日至 8 月10 日的高温天气的频率明显高于 8 月 8 日至 8 月 24日. 上例说明 , 当总体很大或不便于获得时 , 可以用样本的频率分布估计总体的频率分布 . 我们把反映总体频率分布的表格称为频率分布表 . 初中数学已经介绍了历史上所做的抛掷硬币的试验 , 并获得了正面向上或反面向上的频率分布表 . 这类试验只有两种结果,比较简单 . 下面研究较为复杂的频率分布表的制作方法 .例 1 . 从某校高一年级的 1002 名学生中用系统抽样的方法抽取一个容量为 100 的身高样本 , 数据如下 ( 单位 : cm ) . 试作出该样本的频率分布表 .分 析 :该组数据中最小值为 151 , 最大值为 180 , 它们相差 29 , 可取区间 [ 150.5 , 180.5 ] , 并将此区间分成 10 个小区间 , 每个小区间长度为 3 , 再统计出每个区间内的频数并计算相应的频率 . 我们将整个取值区间的长度称为全距 , 分成的区间的长度称为组距 .解:( 1 ) 在全部数据中找出最大值 180 和最小值 151 , 则两者之差为 29 , 确定全距为 30 , 决定以组距 3 将区间[ 150.5 , 180.5 ] 分成 10 个组 ;( 2 ) 从第一组 [ 150.5 , 153.5 ] 开始 , 分别统计各组中的频数 , 再计算各组的频率 , 并将结果填入下表 :分 组频数累计频 数频 率合 计 这张表给出了该身高样本处于各区间内的人数和频率,由此可估计该校高一学生的分布状况 . 一般地 , 编制频率分布表的步骤如下 :( 1 ) 求全距 , 决定组数和组距 , 组距 = 全距 / 组数 ;( 2 ) 分组 , 通常对组内数值所在区间取左闭右开区间 , 最后一组取闭区间 ;( 3 ) 登记频数 , 计算频率 , 列出频率分布表 .练习1.下面是不同厂家生产的手提电脑的重量 ( 单位 : kg ) ,试列出其频率分布表 :分 组频 数频 率201合 计练习2 .一个容量为20的数据样本 , 分组与频数为 :[ 10 , 20 ] 2 个 、 ( 20 , 30 ] 3 个 、 ( 30 , 40 ]4个 、 ( 40 , 50 ] 5 个 、 ( 50 , 60 ] 4 个 、 ( 60 , 70 ]2个 ,则样本数据在区间 ( - ∞ , 50 ] 上的可能性为( )A. 5 %B. 25 %C. 50 %D. 70 %D练习3.在一本书中 ,分组统计 100个句子中的字数 , 得出下列结果 :字数 1 - 5 个的 15 句 , 字数 6 - 10 个的 27 句 , 字数 11 - 15 个的 32 句 , 字数 16 - 20 个的 15 句 , 字数 21 - 25 个的 8 句 , 字数 26 - 30 个的 3 句 . 请作出字数的频率分布表 , 并利用组中值对该书中平均每个句子包含的字数作出估计 .分 组频 数频 率1001合 计6.2.2 频率分布直方图与折线图 例 2 . 下表是某学校一个星期中收交来的失物件数 , 请将 5 天中收交来的失物数用条形图表示 .一二三四五 我们可以利用直方图反映样本的频率分布规律 , 这样的直方图称为频率分布直方图 , 简称频率直方图 . 下面用例 1中的数据加以说明 .例 2 . 作出例 1 中数据的频率分布直方图 .(2) 在横轴上标上 150.5 , 153.5 , 156.5 , ··· , 180.5 表示的点 ( 为方便起见 , 起始点 150.5 可适当前移 ) ;身高 / cm 一般地 , 作频率分布直方图的方法为 : 把横轴分成若干段 , 每一线段对应一个组的组距 , 然后以此线段为底作一矩形 , 它的高等于该组的 ( 频率/组距 ) , 这样得出一系列的矩形 , 每个矩形的面积恰好是该组上的频率 . 这些矩形就构成了频率分布直方图 . 频率直方图比频率分布表更直观 、形象地反映了样本的分布规律 , 如在 164 附近达到 “峰值” , 并具有一定的对称性 , 这说明这批学生的身高在 164 cm 附近较为集中 . 另外还可看出 , 特别高和特别矮的学生都很少 . 如果将频率分布直方图中各相邻的矩形的底边的中点顺次连结起来 , 就得到一条折线 , 我们称这条折线为本组数据的频率折线图 . 例3 的频率直方图中 , 取各相邻矩形的上底边中点并顺次连结 , 再将矩形的边去除 , 得频率折线图如下 : 频率折线图的优点是它反映了数据的变化趋势 . 如果将样本容量取得足够大 , 分组的组距取得足够小 , 则这条折线将趋于一条曲线 , 我们称这一曲线为总体分布的密度曲线 . 如例 3 的频率分布密度曲线可近似地表示为下图 :例 4 . 为了了解一大片经济林的生长情况 , 随机测量其中的100 株的底部周长 , 得到如下数据表 ( 长度单位 : cm ) :( 1 ) 编制频率分布表 ;( 2 ) 绘制频率分布直方图 ;( 3 ) 估计该片经济林中底部周长小于 100 cm 的树木约占多少 , 周长不小于120 cm 的树木约占多少 .解 :( 1 ) 从表中可以看出 , 这组数据的最大值为 135 , 最小值为 80 , 故全距为 55 , 可将其分为 11 组 , 组距为 5 .分 组频 数频 率频率/组距合 计10010.2( 2 ) 这组数据的频率直方图如下图 :周长 / cm( 3 ) 从频率分布表可以看出 , 该样本中小于 100 的频率为0.01 + 0.02 + 0.04 + 0.14 = 0.21 , 不小于 120 的频率为0.11 + 0.06 + 0.02 = 0.19 , 故可估计该片经济林中底部周长小于 100 cm的树木约占 21 % , 周长不小于 120 cm的树木约占 19 % .练习1.作出习题 6.1 第 4 题和第 5 题中数据的频率分布直方图 、频率折线图 .练习2 .为了了解一批灯泡 ( 共 10000 只 ) 的使用寿命 , 从中抽取了 100 只进行测试 , 其使用寿命如下表 :使用寿命/h只 数( 1 ) 制作频率分布表 ;( 2 ) 绘制频率分布直方图 ;( 3 ) 根据样本的频率分布 ,估计使用寿命不低于 1000 / h 的灯泡约有多少只 ?解 :( 1 ) 频率分布表为 :时 间 / h数 量频 率合 计1001( 2 ) 频率分布直方图为:周长 / cm( 3 ) 因为使用寿命不低于 1000 / h 的频率为 0.25 , 所以估计不低于 1000/h 的灯泡约有 5200 只 .6.2.3 茎 叶 图 某蓝球运动员在某赛季各场比赛的得分情况如下 :12 , 15 , 24 , 25 , 31 , 31 , 36 , 36 , 37 , 39 , 44 , 49 , 50 .如何分析该运动员的整体水平及发挥的稳定程度 ? 初中统计部分曾经学过用平均数 、众数和中位数反映总体水平 , 用方差考察稳定程度 . 我们还有一种简易的方法 ,就是将这些数据有条理地列出来 , 从中观察得分的分布情况.这种方法就是画出该运动员得分的茎叶图 . 制作茎叶图的方法是 : 将所有两位数的十位数字作为 “ 茎 ” , 个位数字作为 “ 叶 ” , 茎相同者共用一个茎 , 茎按从小到大的顺序从上向下列出 , 共茎的叶一般按从大到小 ( 或从小到大 ) 的顺序同行列出 .上述运动员的得分茎叶图可用下图表示 : 上图中第一行分界线的左边的 “ 1 ” 表示十位数字 , 右边的 “ 2 ” 和“ 5 ” 表示个为数字 , 这一行说明该运动员的得分为 12 分和 15 分 . 同理,第二行说明得分为 24 分和 25 分 , 第三行说明有两个 31 分 , 两个 36 分 ,一个 37 分 , 一个 39 分 , 依此类推 . 从上面的图可以看出 , 该运动员平均得分及中位数 , 众数都在 20 到 40 之间 , 且分布较对称,集中程度高 , 说明其发挥比较稳定 .茎叶图既可以分析单组数据 , 也可以对两组数据进行比较.例 5 . 甲 、乙两蓝球运动员上赛季每场比赛的得分如下 , 试比较这两位运动员的得分水平 .甲 1 2 , 1 5 , 24 , 25 , 3 1 , 3 1 , 36 , 36 , 37 , 39 , 44 , 49 , 50 .乙 8 , 1 3 , 1 4 ,1 6 , 23 , 26 , 28 , 33 , 38 , 39 , 5 1 .解 :画出两人得分的茎叶图 , 为便于对比分析 , 可将茎放在中间共用 , 叶分列左 、右两侧 :甲乙 第二行表示甲得分为 15 分 、12 分 ,乙得分为 13 分 、14分 、16分 . 其他各行与此类同 . 从这个茎叶图可以看出 , 甲运动员的得分大致对称 , 平均得分 、众数及中位数都是30 多分 . 乙运动员的得分除一个 51 分外 , 也大致对称 , 平均得分 、众数及中位数都是20 多分 . 因此甲发挥比较稳定 , 总体得分情况比乙好 . 用茎叶图刻画数据有两个优点 : 一是所有的信息都可以从图中得到 , 二是记录和表示 .但表示三位数以上的数据时不够方便 .练习1 .2002-2003赛季 ,一球员在 NBA 某些场次的比赛所得蓝板球数分别为:16 , 6 , 3 , 5 , 12 , 8 , 13 , 6 , 10 , 3 , 19 , 14 , 9 , 7 , 10 , 10 , 9 , 11 , 6 , 11 , 12 , 14 , 8 , 6 , 10 , 5 , 10 , 11 , 13 , 9 , 10 , 10 , 7 , 6 , 11 , 12 , 17 , 4 , 12 , 8 , 10 , 12 , 9 , 15 , 15 , 12 , 13 , 18 , 8 , 16 , 请制作这些数据的茎叶图 .3 3 4 5 5 6 6 6 6 6 7 7 8 8 8 8 9 9 9 90 0 0 0 0 0 0 0 1 1 1 1 2 2 2 2 2 2 3 3 3 4 4 5 5 6 6 7 8 9练习2 .下面是甲 、乙两名运动员某赛季一些场次得分的茎叶图 :甲乙( 1 ) 甲乙两名队员的最高得分各是多少 ?( 2 ) 哪名运动员的成绩好一些 ?( 1 ) 甲运动员的最高得分为 51 分 ,乙运动员的最高分为 52 分 ;( 2 ) 甲运动员的成绩好于乙运动员 .习 题 6 . 21 . 某射手在同一条件下射靶 30 次 , 其中 6 环或 6 环以下 2次 , 7 环 6 次 , 8 环 7 次 , 9 环 10 次 , 10 环 5 次 .( 1 ) 列出频率分布表 ;( 2 ) 根据上述结果 , 估计射手射中 7 - 9 环的可能性 .分 组频 数频 率合 计301( 2 )估计射手射中 7 - 9 环的可能性为 76.7% .2 . 从大量棉花中抽取 50 根棉花纤维 , 纤维长度 ( 单位 : mm ) 的数据分组及各组的数频为 :[ 22.5 , 25.5 ) , 3 ; [ 25.5 , 28.5 ) , 8 ; [ 28.5 , 31.5 ) , 9 ; [ 31.5 , 34.5 ) , 11 ; [ 34.5 , 37.5 ) , 10 ; [ 37.5 , 40.5 ) , 5 ; [ 40.5 , 43.5 ] , 4 .( 1 ) 列出样本的频率分布表 ;( 2 ) 画出频率分布直方图 ;( 3 ) 估计纤维长度小于 36 的百分比 .( 1 ) 频率分布表为:解 :分 组频 数频 率合 计501( 2 ) 频率分布直方图为:周长 / cm( 3 ) 对区间 [ 34.5 , 37.5 ) , 组中值为 36 , 这样可估计长度小于 36 mm的频数约为 36 , 频率约为 72 % .3. 为了检测某种产品的质量 , 抽取了一个容量为 100 的样本 ,数据的分组及频数如下表 :分 组频 数频 率合 计( 1 ) 完成上面的频率分布表 ;( 2 ) 画出频率分布直方图 ;( 3 ) 估计数据落在 [ 10.95 , 11.35 ) 范围内的可能性是百分之几 ?0.030.090.130.160.260.200.070.040.021习 题 课1 . 一个容量为 32 的样本 , 已知某组样本的频率为 0.375 , 则该组样本的频数为 ( )分析 : 因为 频数 / 容量 = 频率 , 所以 频数为 32 × 0 . 375 = 12 .C7 . 从一批产品中抽取 50 个 , 然后又在这 50 个产品中抽取 10 个进行检测 , 发现有一个次品 . 则这批产品的合格率估计为分析 : 次品占 0 . 1 , 则合格品估计占 0 . 9 . 90 % 8 . 有容量为 50 的样本 , 数据的分组及各组的频数如下 :[ 10 , 12 ) , 3 ; [ 12 , 14 ) , 5 ; [ 14 , 16 ) , 9 ; [ 16 , 18 ) , 12 ; [ 18 , 20 ) , 10 ; [ 20 , 22 ) , 8 ; [ 22 , 24 ] , 3 .( 1 ) . 列出样本的频率分布表 ;( 2 ) . 估计总体在 [ 12 , 20 ) 的频率 .解 : ( 1 ) . 样本的频率分布表如下 ;分 组 频 数 频 率 合 计 501( 2 ) . 总体在 [ 12 , 20 ) 的频率为 0.10 + 0.18 + 0.24 + 0.20 = 0.72 .9 . 为了了解某市中学生的身体发展情况 , 对某中学的 50 名男生抽样测量 , 其身高记录如下 ( 单位 : cm ) :(1)列出频率分布表 ;(2)估计身高在 168.5 - 176.5 cm 的频率 ;(3)估计身高超过 178.5 cm 的频率 .分 组 频 数 频 率 ( 1 ) 全距为 24 , 确定分 6 组,组距为 4 ;合 计 501( 2 ) 身高在 168.5 - 176.5 cm 的频率为 0.50 ;( 3 ) 身高超过 178.5 cm 的频率为 0.08 .10 . 如图 , 是甲 、乙两学习小组一次测验的成绩的茎叶图 , 试比较这两组学生的学习成绩 .甲乙解: 由茎叶图可以看出 , 甲组的学生成绩比较集中 , 且中位数 ,众数 , 平均数都在 80 多分以上 ;乙组学生的成绩比较对称,中位数 , 众数 , 平均数都在 70 多分以上 , 所以甲组学生的成绩比乙组的好 .11 . 甲 、乙两人同时生产内径为 25.40 mm 的一种零件 , 为了对两人的生产质量进行评比 , 从他们生产的零件中抽出 10 件 ,量得其内径尺寸如下 ( 单位 : mm ) :甲 : 25.46 25.32 25.45 25,39 25.36 25.34 25.42 25.45 25.38 25.42乙 : 25.40 25.43 25.44 25,48 25.48 25.47 25.49 25.31 25.43 25.32从生产的零件内径的尺寸看 , 试用茎叶图比较两人生产的零件的质量 .解: 甲乙25.325.498642655221203347889 从图中可看出 , 甲的零件尺寸比较对称 , 且在 25.40 附近摆动 , 而乙的零件尺寸不对称 , 且中位数与众数都在 25.40 以上 , 相比较 , 甲比乙稳定些 .12 . 容量为 100 的某个样本数据拆分为 10 组 , 并填写频率分布表 , 若前七组频率之和为 0 .79 , 而剩下的三组的频率依次大 0 . 05 , 则剩下的三组中频率最大的一组的频率为分析 : 剩下三组的频率之和为 1 – 0 .79 = 0 . 21 ,设剩下的三组中频率最小的为 a , 则另两组为a + 0.05 , a + 0.1 , 即 a + a + 0.05 + a + 0.1 = 0 . 21解得 a = 0 . 02 , 所以最大的频率为 0 . 12 .2 . 已知样本 6 , 5 , 7 , 7 , 11 , 9 , 10 , 8 , 10 , 8 , 6 , 13 , 11 , 5 , 9 , 12 , 8 , 10 , 5 , 7 . 那么这组样本数据落在范围 7 . 5 - 10 . 5 内的频率为 ( )分析 : 因为 频率 = 频数 / 容量 , 所以 频数为 8 / 20 = 0 . 40 .D3 . 一个容量为 n 的样本 , 已知某组的频率为 0 . 25 , 频树为 5 ,则 n = ( )分析 : 因为 频率 = 频数 / 容量 , 所以 n = 5 / 0 . 25 = 20 .B4 . 对 n 个数据进行整理的频率分布表中 , 各组的频率之和与频数之和分别为 ( )分析 : 频率之和为 1 , 频数之和为 n . C分析 : 由上可得 6 / 60 + 9 / 60 = 1 / 4 .B6 . 样本容量是 40 , 共分成 6 组 , 第 1 - 4 组的频数分别为10 , 5 , 7 , 6 , 第 5 组的频率是 0.10 , 则第 6 组的频率是分析 : 设第 6 组的频率为 x ,因为 10 / 40 + 5 / 40 + 7 / 40 + 6 / 40 + 0.10 + x = 1 ,所以 x = 1 – 0 . 8 = 0 . 2 . 0 . 2