沪教版(上海)八年级数学下册 22.3 特殊的平行四边形 单元教学设计(表格式)
文档属性
| 名称 | 沪教版(上海)八年级数学下册 22.3 特殊的平行四边形 单元教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 16:31:07 | ||
图片预览




文档简介
特殊的平行四边形 单元设计
单元规划
单元名称 特殊的平行四边形
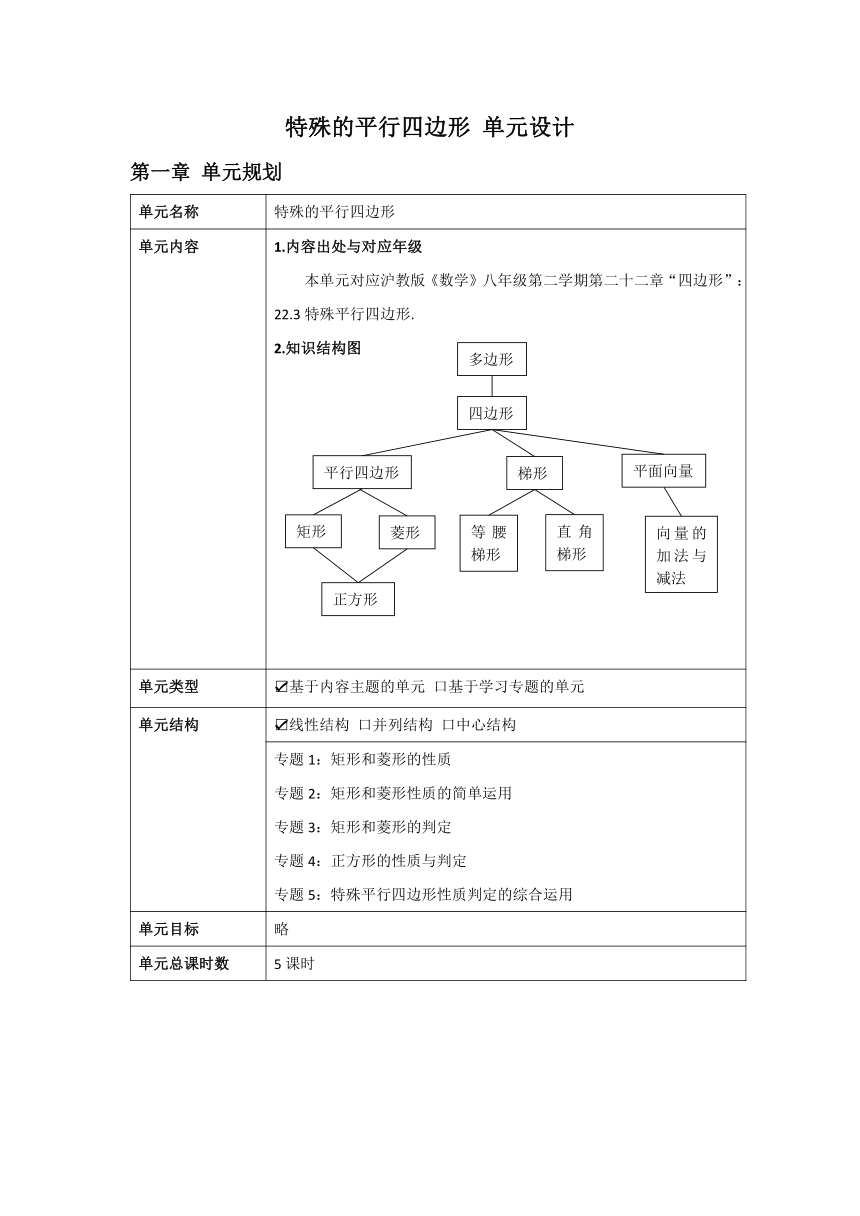
单元内容 1.内容出处与对应年级 本单元对应沪教版《数学》八年级第二学期第二十二章“四边形”:22.3特殊平行四边形. 2.知识结构图
单元类型 基于内容主题的单元 口基于学习专题的单元
单元结构 线性结构 口并列结构 口中心结构
专题1:矩形和菱形的性质 专题2:矩形和菱形性质的简单运用 专题3:矩形和菱形的判定 专题4:正方形的性质与判定 专题5:特殊平行四边形性质判定的综合运用
单元目标 略
单元总课时数 5课时
二、单元教材教法分析
学情分析属性表
分析要点 主要方法
认知基础 学习特点 经验判断法 观察法 调查访谈法 资料分析法 测试法
分析与说明: 本单元主要是研究矩形、菱形、正方形、梯形等特殊的四边形,在这之前学生已经有了一定平行线、三角形、平行四边形等知识储备。本单元初始阶段在证明角相等、线段相等,求线段长、角的度数等有关问题时,受思维定势影响,学生往往还是会走“全等三角形”的老路,教师应有意识的引导、针对性的训练,以构建学生头脑中新的知识网络。本单元特殊平行四边形概念多易混淆,不易理清它们的从属关系,性质及判定方法不易区分,推理证明时易造成逻辑上的混乱,教学时,可借助“集合”图示理清它们之间的从属关系。在图形性质及判定方法的教学中,可借助实物、几何画板等教学软件让学生充分感受知识的产生、发展及演变过程;本单元逻辑推理论证能力的培养是重点也是难点,受学生的说理能力、逻辑思维水平的限制,学生在陈述问题的解决过程时,可能出现图形性质与判定方法混淆、判定条件不全强行推理过渡等现象,教师可通过小组评阅、学生说理过程板眼、规范证明过程展示等多种形式对学生的解答有针对性的进行调整,宜采用个别指正和集体评阅相结合的方式进行。
内容解析
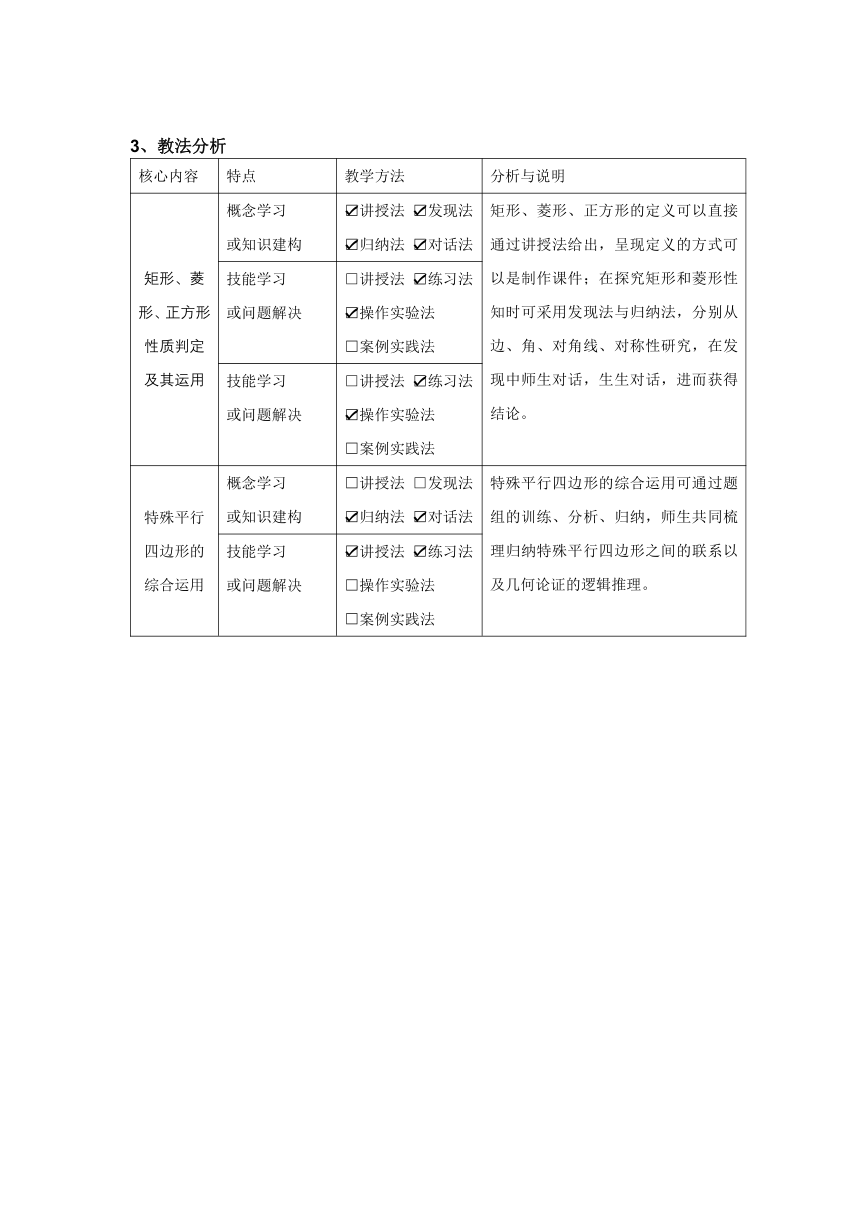
3、教法分析
核心内容 特点 教学方法 分析与说明
矩形、菱形、正方形性质判定及其运用 概念学习 或知识建构 讲授法 发现法 归纳法 对话法 矩形、菱形、正方形的定义可以直接通过讲授法给出,呈现定义的方式可以是制作课件;在探究矩形和菱形性知时可采用发现法与归纳法,分别从边、角、对角线、对称性研究,在发现中师生对话,生生对话,进而获得结论。
技能学习 或问题解决 □讲授法 练习法 操作实验法 案例实践法
技能学习 或问题解决 □讲授法 练习法 操作实验法 案例实践法
特殊平行四边形的综合运用 概念学习 或知识建构 讲授法 □发现法 归纳法 对话法 特殊平行四边形的综合运用可通过题组的训练、分析、归纳,师生共同梳理归纳特殊平行四边形之间的联系以及几何论证的逻辑推理。
技能学习 或问题解决 讲授法 练习法 操作实验法 案例实践法
三、单元目标设计
研读与筛选
单元目标设计学习内容与要求汇总表
课标描述 学习内容 具体要求 学
理解矩形、菱形、正方形的概念,知道它们的内在关系,体会集合思想;掌握矩形、菱形、正方形的特殊性质和判别方法,并能运用这些知识进行简单的有关证明和计算;结合特殊四边形性质和判定方法以及相关问题的证明,进一步发展逻辑思维能力和推理论证能力。 矩形、菱形、正方形的定义、性质、判定 掌握矩形、菱形、正方形的概念,掌握矩形、菱形、正方形的性质定理和判定定理. B理解
运用性质判定解决几何问题 会用平行四边形、矩形、菱形、正方形的判定定理和性质定理解决简单的几何问题. C运用
2、细化与分解
(1)单元目标设计知识与技能目标属性表
序号 知识与技能目标表述 学 单元课序
1 会识别矩形和菱形,知识它们之间的关系以及它们与平行四边形的关系 A识记B理解 C运用D综合 1
2 会用文字语言和符号语言表示矩形、菱形的性质定理 A识记B理解 C运用D综合 1
3 会用矩形、菱形的性质定理进行简单的几何计算 A识记B理解 C运用D综合 1
4 会通过矩形菱形的性质运用,掌握处理矩形菱形的一般方法 A识记B理解 C运用D综合 1
5 会运用矩形、菱形的有关性质进行有关的证明和计算 A识记B理解 C运用D综合 2
6 会用文字语言和符号语言表示矩形、菱形的判定定理 A识记B理解 C运用D综合 3
7 会用矩形、菱形的判定定理进行有关的证明 A识记B理解 C运用D综合 3
8 会识别正方形,知道它与矩形、菱形以及平行四边形之间的关系 A识记B理解 C运用D综合 4
9 会用文字语言和符号语言表示正方形的性质定理与判定定理 A识记B理解 C运用D综合 4
10 会运用正方形的性质定理和判定定理进行有关的证明和计算 A识记B理解 C运用D综合 5
11 会识别正方形与矩形、菱形以及与平行四边形之间的关系 A识记B理解 C运用D综合 5
12 综合运用特殊平行四边形的性质与判定解决简单的几何问题 A识记B理解 C运用D综合 5
(2)单元目标设计过程与方法目标属性表
序号 过程与方法目标表述 能力水平 单元课序
1 经历从平行四边形到矩形、菱形的研究过程,体验“从一般到特殊”的研究方法,知道矩形、菱形之间的关系以及它们与平行四边形的联系与区别. 运算求解 推理论证空间想象 数学表达 数据处理 数学建模 1
2 通过将矩形、菱形转化为直角三角形或等腰三角形解决数学问题的过程,体会转化思想. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 2
3 经历探索矩形和菱形的判定方法的过程,发展逻辑思维能力. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 3
4 经历探讨正方形的性质及其判定的过程,感悟类比思想、分类讨论思想以及“从一般到特殊”的方法. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 4
5 经历运用特殊平行四边形的性质定理判定定理,进一步发展逻辑思维能力和推理论证能力. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 5
(3)单元目标设计情感态度与价值观目标属性表
序号 情感态度与价值观目标表述 育人价值的视角 单元课序
1 通过探索特殊平行四边形的性质和判定,获得从事数学活动的经验和体验,提高合情推理能力. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 1,3,4
2 通过分析平行四边形与特殊平行四边形概念之间的联系与区别,认识特殊与一般的关系,从中体会事物之间总是互相联系又互相区别的辩证唯物主义观点. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 1,4
3 经历探索正方形有关性质和四边形成为正方形的条件过程,提高学生动手操作的能力、主动探究的习惯和合作交流的意识. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 4
单元活动设计
1、整体规划
编号 活动主题 活动目标
1 建立四边形学习档案 通过建立四边形学习档案,强化几何图形学习的一般规律,建立整体意识,将知识结构化系统化,并促进学生自主学习交流,培养自主学习的能力.
2 特殊平行四边形之间的联系与区别 通过设计三个题组,从边、角、对角线的变化来研究特殊平行四边形,从特殊平行四边形不同的判定方法进一步发展逻辑推理能力与空间想象能力.
3 特殊平行四边形的证明 运用特殊平行四边形之间的性质定理与判定定理解决数学问题,通过文字语言、图形语言、几何语言三种文字之间的转化,提高数学表达能力与推理能力.
活动1:
活动主题 建立四边形学习档案
活动目标 通过建立四边形学习档案,强化几何图形学习的一般规律,建立整体意识,将知识结构化系统化,并促进学生自主学习交流,培养自主学习的能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 通过第一课时的学习,学生课后按照“平行四边形小档案”的范例,自主完成矩形与菱形的小档案.
活动类型 新知建构活动
活动空间 课外活动
活动资源 文本
活动指导 活动方式 建议学生仿照平行四边形小档案,自主完成矩形与菱形档案,并在后续能继续研究正方形的小档案,与此同时,建议教师对于后期的梯形、针形、对角线有特殊性的图形都建立档案,形成学生自主学习资料.
活动2:
活动主题 特殊平行四边形的证明
活动目标 运用特殊平行四边形之间的性质定理与判定定理解决数学问题,通过文字语言、图形语言、几何语言三种文字之间的转化,提高数学表达能力与推理能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 完成2组几何证明,在学习单上进行图形语言、几何语言、文字语言三种语言的不断转化. 题组一: 1、如图,已知OM、ON分别是∠AOB及其外角的平分线,P是∠MON内部任意一点,过点P作PE、PF分别垂直于OM、ON,垂足分别为E、F.
求证:四边形PEOF是矩形. 2、如图EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别相交于点E、F. 求证:四边形BFDE是菱形. 要求: (1)教师规范示范 (2)学生独立思考 (3)师生共同分析思路 (4)归纳几何证明的基本思路 题组二: 3、如图,在平行四边形ABCD中,AB⊥BD,点M、N分别为边AD与BC的中点 求证:四边形BMDN是菱形. 4、如图,已知,点是的中点,点是的中点,过点作∥交的延长线于点,联结、. 求证:四边形是矩形. 要求: 学生独立思考 学生分析交流
活动类型 问题探究活动
活动空间 课内活动
活动资源 文本
活动指导 活动方式 建议教师在题组一中的1引导学生通过读题形成图形语言,进行思路分析,第2题则尝试让学生独立思考,相互之间说说自己的思路,并全班交流,并完成格式书写,题组二则有学生独立完成.
活动3:
活动主题 特殊平行四边形之间的关系
活动目标 通过设计三个题组,从边、角、对角线的变化来研究特殊平行四边形,从特殊平行四边形不同的判定方法进一步发展逻辑推理能力与空间想象能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 1、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD, 等边△ACE、等边△BCF. (1)求证:四边形DAEF是平行四边形; (2)探究下列问题:(只填满足的条件,不需证明) ①当△ABC满足_________条件时,四边形DAEF是矩形; ②当△ABC满足_________条件时,四边形DAEF是菱形; ③当△ABC满足_________条件时,以D、A、E、F为顶点的四边形不存在. 2、如图,任意四边形ABCD,对角线AC、BD交于O点,过各顶点分别作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH的形状会有哪些变化?完成以下题目: (1)①当ABCD为任意四边形时,EFGH为___________; ②当ABCD为矩形时,EFGH为___________; ③当ABCD为菱形时,EFGH为___________; ④当ABCD为正方形时,EFGH为___________; (2)请对(1)中①②你所写的结论进行证明. (3)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件? 3、如图,在四边形ABCD中,点E、F是对角线BD上, 且BE = FD,联结AE、AF、CE、CF. (1)若四边形ABCD是正方形, 求证:四边形AECF是菱形. (2)若四边形ABCD是平行四边形, 那么四边形AECF是什么图形? (3)若四边形AECF是菱形, 那么四边形ABCD还是正方形?
活动类型 问题探究活动
活动空间 课内活动
活动资源 文本
活动指导 活动方式 建议例题1教师带领学生复习巩固平行四边形、矩形、菱形的判定方法;例2、例3则是由学生独立思考、合作交流完成.
单元作业
1、整体规划
单元作业类型 单元作业内容
课时作业 专题1:矩形和菱形的性质 专题2:矩形和菱形性质的简单运用 专题3:矩形和菱形的判定 专题4:正方形的性质与判定 专题5:特殊平行四边形性质判定的综合运用
2、属性表
确定单元作业目标
序号 单元作业目标描述 学 单元课序
1 会识别矩形和菱形,知识它们之间的关系以及它们与平行四边形的关系 A 1
2 会用文字语言和符号语言表示矩形、菱形的性质定理 A
3 会用矩形、菱形的性质定理进行简单的几何计算 C
4 会通过矩形菱形的性质运用,掌握处理矩形菱形的一般方法 B 2
5 会运用矩形、菱形的有关性质进行有关的证明和计算 C
6 会用文字语言和符号语言表示矩形、菱形的判定定理 A 3
7 会用矩形、菱形的判定定理进行有关的证明 C
8 会识别正方形,知道它与矩形、菱形以及平行四边形之间的关系 B 4
9 会用文字语言和符号语言表示正方形的性质定理与判定定理 A
10 会运用正方形的性质定理和判定定理进行有关的证明和计算 C
11 会识别正方形与矩形、菱形以及与平行四边形之间的关系 B 5
12 综合运用特殊平行四边形的性质与判定解决简单的几何问题 C
六、单元评价设计(目前无法填写)
1.评价项目设计属性表
编号
评价目标
评价内容
评价要素 评价主体
评价时间
评价类型
评价项目
评价工具
评价结果
使用说明
单元评价设计汇总表
编号 评价主体 评价时间 评价类型 评价项目 评价工具 评价结果
七、单元资源设计
1.单元资源汇总表
序号 资源名称 资源用途 资源形式
1 特殊四边形小档案 学生自主建立几何图形学习的档案 文稿
2 几何图形知识树 直观的看到几何图形的变化以及相互之间的联系与区别 微课
3 几何证明分析表 提高学生在三种数学语言间的转化,提高逻辑推理能力 文稿
单元规划
单元名称 特殊的平行四边形
单元内容 1.内容出处与对应年级 本单元对应沪教版《数学》八年级第二学期第二十二章“四边形”:22.3特殊平行四边形. 2.知识结构图
单元类型 基于内容主题的单元 口基于学习专题的单元
单元结构 线性结构 口并列结构 口中心结构
专题1:矩形和菱形的性质 专题2:矩形和菱形性质的简单运用 专题3:矩形和菱形的判定 专题4:正方形的性质与判定 专题5:特殊平行四边形性质判定的综合运用
单元目标 略
单元总课时数 5课时
二、单元教材教法分析
学情分析属性表
分析要点 主要方法
认知基础 学习特点 经验判断法 观察法 调查访谈法 资料分析法 测试法
分析与说明: 本单元主要是研究矩形、菱形、正方形、梯形等特殊的四边形,在这之前学生已经有了一定平行线、三角形、平行四边形等知识储备。本单元初始阶段在证明角相等、线段相等,求线段长、角的度数等有关问题时,受思维定势影响,学生往往还是会走“全等三角形”的老路,教师应有意识的引导、针对性的训练,以构建学生头脑中新的知识网络。本单元特殊平行四边形概念多易混淆,不易理清它们的从属关系,性质及判定方法不易区分,推理证明时易造成逻辑上的混乱,教学时,可借助“集合”图示理清它们之间的从属关系。在图形性质及判定方法的教学中,可借助实物、几何画板等教学软件让学生充分感受知识的产生、发展及演变过程;本单元逻辑推理论证能力的培养是重点也是难点,受学生的说理能力、逻辑思维水平的限制,学生在陈述问题的解决过程时,可能出现图形性质与判定方法混淆、判定条件不全强行推理过渡等现象,教师可通过小组评阅、学生说理过程板眼、规范证明过程展示等多种形式对学生的解答有针对性的进行调整,宜采用个别指正和集体评阅相结合的方式进行。
内容解析
3、教法分析
核心内容 特点 教学方法 分析与说明
矩形、菱形、正方形性质判定及其运用 概念学习 或知识建构 讲授法 发现法 归纳法 对话法 矩形、菱形、正方形的定义可以直接通过讲授法给出,呈现定义的方式可以是制作课件;在探究矩形和菱形性知时可采用发现法与归纳法,分别从边、角、对角线、对称性研究,在发现中师生对话,生生对话,进而获得结论。
技能学习 或问题解决 □讲授法 练习法 操作实验法 案例实践法
技能学习 或问题解决 □讲授法 练习法 操作实验法 案例实践法
特殊平行四边形的综合运用 概念学习 或知识建构 讲授法 □发现法 归纳法 对话法 特殊平行四边形的综合运用可通过题组的训练、分析、归纳,师生共同梳理归纳特殊平行四边形之间的联系以及几何论证的逻辑推理。
技能学习 或问题解决 讲授法 练习法 操作实验法 案例实践法
三、单元目标设计
研读与筛选
单元目标设计学习内容与要求汇总表
课标描述 学习内容 具体要求 学
理解矩形、菱形、正方形的概念,知道它们的内在关系,体会集合思想;掌握矩形、菱形、正方形的特殊性质和判别方法,并能运用这些知识进行简单的有关证明和计算;结合特殊四边形性质和判定方法以及相关问题的证明,进一步发展逻辑思维能力和推理论证能力。 矩形、菱形、正方形的定义、性质、判定 掌握矩形、菱形、正方形的概念,掌握矩形、菱形、正方形的性质定理和判定定理. B理解
运用性质判定解决几何问题 会用平行四边形、矩形、菱形、正方形的判定定理和性质定理解决简单的几何问题. C运用
2、细化与分解
(1)单元目标设计知识与技能目标属性表
序号 知识与技能目标表述 学 单元课序
1 会识别矩形和菱形,知识它们之间的关系以及它们与平行四边形的关系 A识记B理解 C运用D综合 1
2 会用文字语言和符号语言表示矩形、菱形的性质定理 A识记B理解 C运用D综合 1
3 会用矩形、菱形的性质定理进行简单的几何计算 A识记B理解 C运用D综合 1
4 会通过矩形菱形的性质运用,掌握处理矩形菱形的一般方法 A识记B理解 C运用D综合 1
5 会运用矩形、菱形的有关性质进行有关的证明和计算 A识记B理解 C运用D综合 2
6 会用文字语言和符号语言表示矩形、菱形的判定定理 A识记B理解 C运用D综合 3
7 会用矩形、菱形的判定定理进行有关的证明 A识记B理解 C运用D综合 3
8 会识别正方形,知道它与矩形、菱形以及平行四边形之间的关系 A识记B理解 C运用D综合 4
9 会用文字语言和符号语言表示正方形的性质定理与判定定理 A识记B理解 C运用D综合 4
10 会运用正方形的性质定理和判定定理进行有关的证明和计算 A识记B理解 C运用D综合 5
11 会识别正方形与矩形、菱形以及与平行四边形之间的关系 A识记B理解 C运用D综合 5
12 综合运用特殊平行四边形的性质与判定解决简单的几何问题 A识记B理解 C运用D综合 5
(2)单元目标设计过程与方法目标属性表
序号 过程与方法目标表述 能力水平 单元课序
1 经历从平行四边形到矩形、菱形的研究过程,体验“从一般到特殊”的研究方法,知道矩形、菱形之间的关系以及它们与平行四边形的联系与区别. 运算求解 推理论证空间想象 数学表达 数据处理 数学建模 1
2 通过将矩形、菱形转化为直角三角形或等腰三角形解决数学问题的过程,体会转化思想. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 2
3 经历探索矩形和菱形的判定方法的过程,发展逻辑思维能力. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 3
4 经历探讨正方形的性质及其判定的过程,感悟类比思想、分类讨论思想以及“从一般到特殊”的方法. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 4
5 经历运用特殊平行四边形的性质定理判定定理,进一步发展逻辑思维能力和推理论证能力. 运算求解 推理论证 空间想象 数学表达 数据处理 数学建模 5
(3)单元目标设计情感态度与价值观目标属性表
序号 情感态度与价值观目标表述 育人价值的视角 单元课序
1 通过探索特殊平行四边形的性质和判定,获得从事数学活动的经验和体验,提高合情推理能力. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 1,3,4
2 通过分析平行四边形与特殊平行四边形概念之间的联系与区别,认识特殊与一般的关系,从中体会事物之间总是互相联系又互相区别的辩证唯物主义观点. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 1,4
3 经历探索正方形有关性质和四边形成为正方形的条件过程,提高学生动手操作的能力、主动探究的习惯和合作交流的意识. 数学与理性 数学与思维 数学与方法 数学与美学 数学与社会 4
单元活动设计
1、整体规划
编号 活动主题 活动目标
1 建立四边形学习档案 通过建立四边形学习档案,强化几何图形学习的一般规律,建立整体意识,将知识结构化系统化,并促进学生自主学习交流,培养自主学习的能力.
2 特殊平行四边形之间的联系与区别 通过设计三个题组,从边、角、对角线的变化来研究特殊平行四边形,从特殊平行四边形不同的判定方法进一步发展逻辑推理能力与空间想象能力.
3 特殊平行四边形的证明 运用特殊平行四边形之间的性质定理与判定定理解决数学问题,通过文字语言、图形语言、几何语言三种文字之间的转化,提高数学表达能力与推理能力.
活动1:
活动主题 建立四边形学习档案
活动目标 通过建立四边形学习档案,强化几何图形学习的一般规律,建立整体意识,将知识结构化系统化,并促进学生自主学习交流,培养自主学习的能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 通过第一课时的学习,学生课后按照“平行四边形小档案”的范例,自主完成矩形与菱形的小档案.
活动类型 新知建构活动
活动空间 课外活动
活动资源 文本
活动指导 活动方式 建议学生仿照平行四边形小档案,自主完成矩形与菱形档案,并在后续能继续研究正方形的小档案,与此同时,建议教师对于后期的梯形、针形、对角线有特殊性的图形都建立档案,形成学生自主学习资料.
活动2:
活动主题 特殊平行四边形的证明
活动目标 运用特殊平行四边形之间的性质定理与判定定理解决数学问题,通过文字语言、图形语言、几何语言三种文字之间的转化,提高数学表达能力与推理能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 完成2组几何证明,在学习单上进行图形语言、几何语言、文字语言三种语言的不断转化. 题组一: 1、如图,已知OM、ON分别是∠AOB及其外角的平分线,P是∠MON内部任意一点,过点P作PE、PF分别垂直于OM、ON,垂足分别为E、F.
求证:四边形PEOF是矩形. 2、如图EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别相交于点E、F. 求证:四边形BFDE是菱形. 要求: (1)教师规范示范 (2)学生独立思考 (3)师生共同分析思路 (4)归纳几何证明的基本思路 题组二: 3、如图,在平行四边形ABCD中,AB⊥BD,点M、N分别为边AD与BC的中点 求证:四边形BMDN是菱形. 4、如图,已知,点是的中点,点是的中点,过点作∥交的延长线于点,联结、. 求证:四边形是矩形. 要求: 学生独立思考 学生分析交流
活动类型 问题探究活动
活动空间 课内活动
活动资源 文本
活动指导 活动方式 建议教师在题组一中的1引导学生通过读题形成图形语言,进行思路分析,第2题则尝试让学生独立思考,相互之间说说自己的思路,并全班交流,并完成格式书写,题组二则有学生独立完成.
活动3:
活动主题 特殊平行四边形之间的关系
活动目标 通过设计三个题组,从边、角、对角线的变化来研究特殊平行四边形,从特殊平行四边形不同的判定方法进一步发展逻辑推理能力与空间想象能力.
适用单元 本活动适用沪教版《数学》八年级第二学期第二十二章“四边形”中“特殊的平行四边形”单元
活动任务 1、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD, 等边△ACE、等边△BCF. (1)求证:四边形DAEF是平行四边形; (2)探究下列问题:(只填满足的条件,不需证明) ①当△ABC满足_________条件时,四边形DAEF是矩形; ②当△ABC满足_________条件时,四边形DAEF是菱形; ③当△ABC满足_________条件时,以D、A、E、F为顶点的四边形不存在. 2、如图,任意四边形ABCD,对角线AC、BD交于O点,过各顶点分别作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH的形状会有哪些变化?完成以下题目: (1)①当ABCD为任意四边形时,EFGH为___________; ②当ABCD为矩形时,EFGH为___________; ③当ABCD为菱形时,EFGH为___________; ④当ABCD为正方形时,EFGH为___________; (2)请对(1)中①②你所写的结论进行证明. (3)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件? 3、如图,在四边形ABCD中,点E、F是对角线BD上, 且BE = FD,联结AE、AF、CE、CF. (1)若四边形ABCD是正方形, 求证:四边形AECF是菱形. (2)若四边形ABCD是平行四边形, 那么四边形AECF是什么图形? (3)若四边形AECF是菱形, 那么四边形ABCD还是正方形?
活动类型 问题探究活动
活动空间 课内活动
活动资源 文本
活动指导 活动方式 建议例题1教师带领学生复习巩固平行四边形、矩形、菱形的判定方法;例2、例3则是由学生独立思考、合作交流完成.
单元作业
1、整体规划
单元作业类型 单元作业内容
课时作业 专题1:矩形和菱形的性质 专题2:矩形和菱形性质的简单运用 专题3:矩形和菱形的判定 专题4:正方形的性质与判定 专题5:特殊平行四边形性质判定的综合运用
2、属性表
确定单元作业目标
序号 单元作业目标描述 学 单元课序
1 会识别矩形和菱形,知识它们之间的关系以及它们与平行四边形的关系 A 1
2 会用文字语言和符号语言表示矩形、菱形的性质定理 A
3 会用矩形、菱形的性质定理进行简单的几何计算 C
4 会通过矩形菱形的性质运用,掌握处理矩形菱形的一般方法 B 2
5 会运用矩形、菱形的有关性质进行有关的证明和计算 C
6 会用文字语言和符号语言表示矩形、菱形的判定定理 A 3
7 会用矩形、菱形的判定定理进行有关的证明 C
8 会识别正方形,知道它与矩形、菱形以及平行四边形之间的关系 B 4
9 会用文字语言和符号语言表示正方形的性质定理与判定定理 A
10 会运用正方形的性质定理和判定定理进行有关的证明和计算 C
11 会识别正方形与矩形、菱形以及与平行四边形之间的关系 B 5
12 综合运用特殊平行四边形的性质与判定解决简单的几何问题 C
六、单元评价设计(目前无法填写)
1.评价项目设计属性表
编号
评价目标
评价内容
评价要素 评价主体
评价时间
评价类型
评价项目
评价工具
评价结果
使用说明
单元评价设计汇总表
编号 评价主体 评价时间 评价类型 评价项目 评价工具 评价结果
七、单元资源设计
1.单元资源汇总表
序号 资源名称 资源用途 资源形式
1 特殊四边形小档案 学生自主建立几何图形学习的档案 文稿
2 几何图形知识树 直观的看到几何图形的变化以及相互之间的联系与区别 微课
3 几何证明分析表 提高学生在三种数学语言间的转化,提高逻辑推理能力 文稿
