人教版数学七上 第二章 整式的加减 单元整合教案+“数字规律”专题研究活动课教案+练习(表格式)
文档属性
| 名称 | 人教版数学七上 第二章 整式的加减 单元整合教案+“数字规律”专题研究活动课教案+练习(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 441.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 17:05:48 | ||
图片预览


文档简介
第二章 整式的加减 单元整合 教案
人教版数学七年级上册
(一)单元整合设计
学科 数学 课型 习题式□ 课题式√ 项目式□
课题 从“摆房子”说起——“数字规律”专题研究
教师 班级
深度 解读 教材 精选教材中最能体现学科本质的知识,充分挖掘教材内容中的五育育人点。 北师大七年级上第三章《整式及其加减》这章,除了必要的知识技能:代数式的定义、整式及整式的加减,就是“探索与表达规律”,其内容在第一节和第五节都有体现。初中生对规律的学习,也基本出自这里。 本章第一节《字母表示数》中用火柴棍摆正方形让学生感受字母可以表示规律,初步形成符号意识。《探索与表达规律》两个课时则通过对图形与数字规律探究,重点关注了事物的一般化表示,学生试着抽象地分析数学对象,符号意识得以发展。教材在这里创设了丰富的问题情境,有日历、摆房子、摆桌椅、数字游戏等,指向学生数学眼光、数学思维、数学语言的培育。但这三个课时涉及的都是等差数列这种特殊的数字规律,事实上,在教材的其他章节,已经出现了等比数列的问题情境,三年的学业评价也会出现更丰富的问题形式。同时,我们还发现,学生对规律的兴趣和需求显然不止于此,他们其实是期待对数字规律能有一个更加清晰的分类与深入的探究。 因此,我们补充了本课,在这里,我们以教材问题“摆房子”为切入口设计了一堂全新的活动课,意在引导学生从图形到数字,探究数字的规律,并用字母表示规律,形成对等差数列、等比数列、平方数列,三角数列的初步认知,强化学生的数感与量感,并在反复用图形去解释描述数字规律中,发展学生的几何直观。
深入 剖析 学情 根据学生在学科学习及五育发展上的起点、薄弱、缺失、障碍和需求,深度分析把握学情。 数字规律对初中生而言一直都是零散的存在,不少学生甚至在孩童时便听过了“高斯求和”、“棋盘摆米”等经典的数学故事,但他们对这些知识的理解仅仅只是故事的层面,尚未健全为数学的表示,更别说形成一个相对完整的知识脉络和思考方式。
五育融合维度 智育√ 德育√ 体育□ 美育√ 劳动教育□
大概念 字母表示数
教学目标 Know(知道什么) 能从现实世界中抽象出简单的数学问题,并试着用字母进行表达; 经历由特殊到一般和由一般到特殊的过程,并能用代数式表示具体问题中数量关系; 3. 能用字母进行规律的一般化表达并验证所探索规律的正确性.
Understand(理解什么)
Do(能做什么)
Be(成为什么)
教学重点 如何进行规律的一般化表达
教学难点 用代数式和图形表示常见数字规律
(二)课时教学设计
课时目标 1. 掌握常见的数字规律,并能从具体的问题背景中抽象出数字规律; 2. 能用代数式表示数字规律,并借助图形表现数字规律; 3. 理解常见数列的一般化表达与求和。
深度 学习 过程 环节设计 活动(任务)设计 设计意图
一、问题引入 用棋子按如图方式摆“房子”:照这样的规律摆下去 (1)摆第10个“房子”需要多少颗棋子? (2)摆第n个需要多少颗棋子?你是如何得到的? (3)用71颗棋子能摆出这样的小房子吗? 过程中鼓励学生从图形和数字两个维度去解释规律,实现多种角度发展学生的思维的目的,并实现数字规律探究的开端。
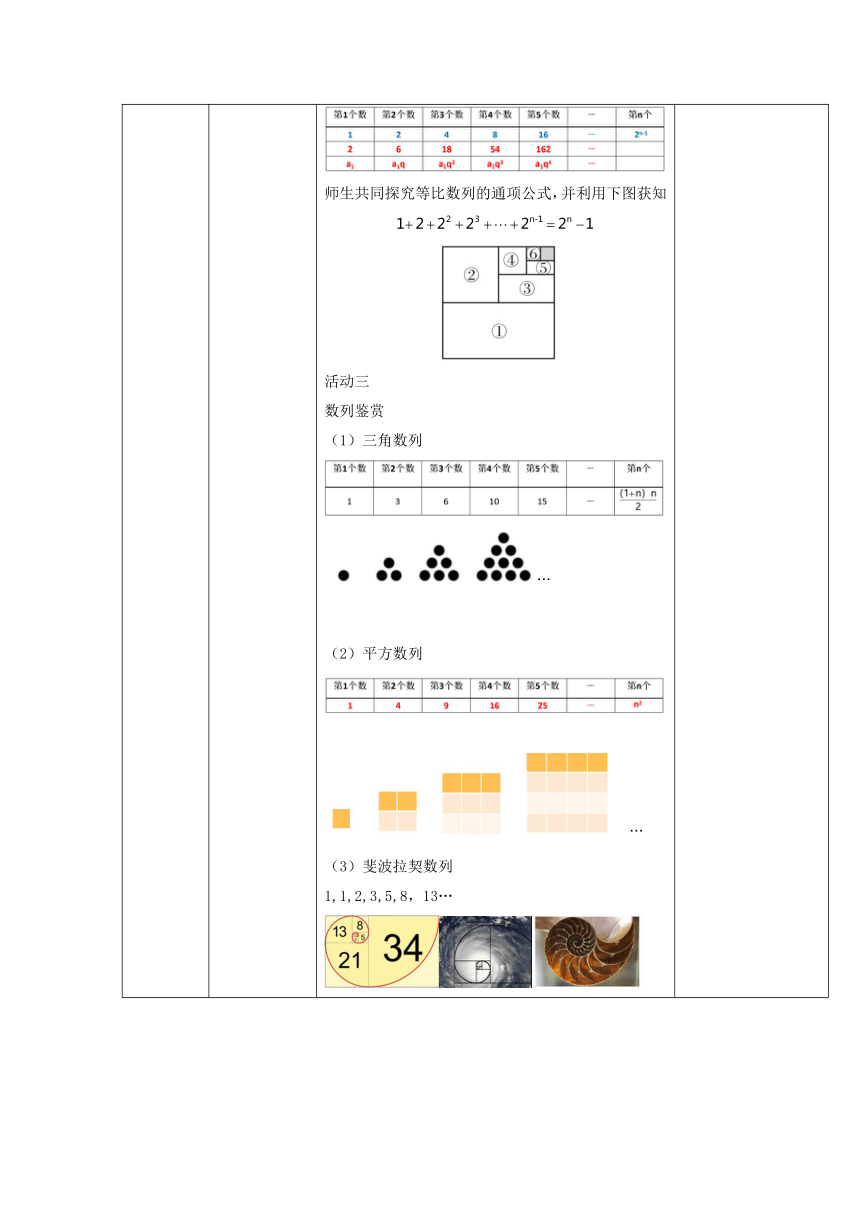
二、新知探究 活动一 问题1:你能不能再说出几个类似的等差数列?并用字母表示这个规律的第n个数吗?关于你写的数列你还能想到什么? 师生共同探究通项公式及求和公式求和公式。 活动二 问题2:观察以下数列,试着用字母表示这个规律的第n个数,除此之外,你还能想到什么? 师生共同探究等比数列的通项公式,并利用下图获知 活动三 数列鉴赏 三角数列 (2)平方数列 (3)斐波拉契数列 1,1,2,3,5,8,13… 学生反复经历“发现规律——表达规律——揭示规律”的过程,利用字母进行规律的一般化表达,并借助图形表达规律,进一步发展学生的符号意识和几何直观。
三、小结回顾 通过本节课的学习,我们学会了什么? 解决规律问题的方法:特殊 一般 特殊 解决规律问题的步骤:观察 猜想 表达 验证 解决规律问题的思想:数形结合 等差数列,等比数列,三角数和平方数的一般化表达 通过小结,建立起本课的知识结构。
配套练习
一、填空题
如图,用相同的圆点按照一定的规律拼出图形,第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点按照此规律,第幅图中圆点的个数是
(用含的代数式表示).
2.如图,下面是用棋子摆成的“”字,按这样的规律摆下去,摆成第个“”字需要 个棋子(用含的代数式表示);摆成第100个“”字需要 个棋子.
3.一个面积为的长方形纸片,第一次截去一半,第二次截去剩下的一半,如此下去,第10次后剩下的面积是 .
4.观察下列一组算式:,,,,,根据你所发现的规律,猜想第个等式为 .
5.有一列数,,,,,那么第n个数是 .
6.如图所示,下列三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中m= (用含n的式子表示).
二、解答题
7.求的值,可令,
则,因此.
仿照以上推理,请你计算出的值.
8.查阅斐波拉契数列的相关资料,说说生活中的那些斐波拉契现象.
人教版数学七年级上册
(一)单元整合设计
学科 数学 课型 习题式□ 课题式√ 项目式□
课题 从“摆房子”说起——“数字规律”专题研究
教师 班级
深度 解读 教材 精选教材中最能体现学科本质的知识,充分挖掘教材内容中的五育育人点。 北师大七年级上第三章《整式及其加减》这章,除了必要的知识技能:代数式的定义、整式及整式的加减,就是“探索与表达规律”,其内容在第一节和第五节都有体现。初中生对规律的学习,也基本出自这里。 本章第一节《字母表示数》中用火柴棍摆正方形让学生感受字母可以表示规律,初步形成符号意识。《探索与表达规律》两个课时则通过对图形与数字规律探究,重点关注了事物的一般化表示,学生试着抽象地分析数学对象,符号意识得以发展。教材在这里创设了丰富的问题情境,有日历、摆房子、摆桌椅、数字游戏等,指向学生数学眼光、数学思维、数学语言的培育。但这三个课时涉及的都是等差数列这种特殊的数字规律,事实上,在教材的其他章节,已经出现了等比数列的问题情境,三年的学业评价也会出现更丰富的问题形式。同时,我们还发现,学生对规律的兴趣和需求显然不止于此,他们其实是期待对数字规律能有一个更加清晰的分类与深入的探究。 因此,我们补充了本课,在这里,我们以教材问题“摆房子”为切入口设计了一堂全新的活动课,意在引导学生从图形到数字,探究数字的规律,并用字母表示规律,形成对等差数列、等比数列、平方数列,三角数列的初步认知,强化学生的数感与量感,并在反复用图形去解释描述数字规律中,发展学生的几何直观。
深入 剖析 学情 根据学生在学科学习及五育发展上的起点、薄弱、缺失、障碍和需求,深度分析把握学情。 数字规律对初中生而言一直都是零散的存在,不少学生甚至在孩童时便听过了“高斯求和”、“棋盘摆米”等经典的数学故事,但他们对这些知识的理解仅仅只是故事的层面,尚未健全为数学的表示,更别说形成一个相对完整的知识脉络和思考方式。
五育融合维度 智育√ 德育√ 体育□ 美育√ 劳动教育□
大概念 字母表示数
教学目标 Know(知道什么) 能从现实世界中抽象出简单的数学问题,并试着用字母进行表达; 经历由特殊到一般和由一般到特殊的过程,并能用代数式表示具体问题中数量关系; 3. 能用字母进行规律的一般化表达并验证所探索规律的正确性.
Understand(理解什么)
Do(能做什么)
Be(成为什么)
教学重点 如何进行规律的一般化表达
教学难点 用代数式和图形表示常见数字规律
(二)课时教学设计
课时目标 1. 掌握常见的数字规律,并能从具体的问题背景中抽象出数字规律; 2. 能用代数式表示数字规律,并借助图形表现数字规律; 3. 理解常见数列的一般化表达与求和。
深度 学习 过程 环节设计 活动(任务)设计 设计意图
一、问题引入 用棋子按如图方式摆“房子”:照这样的规律摆下去 (1)摆第10个“房子”需要多少颗棋子? (2)摆第n个需要多少颗棋子?你是如何得到的? (3)用71颗棋子能摆出这样的小房子吗? 过程中鼓励学生从图形和数字两个维度去解释规律,实现多种角度发展学生的思维的目的,并实现数字规律探究的开端。
二、新知探究 活动一 问题1:你能不能再说出几个类似的等差数列?并用字母表示这个规律的第n个数吗?关于你写的数列你还能想到什么? 师生共同探究通项公式及求和公式求和公式。 活动二 问题2:观察以下数列,试着用字母表示这个规律的第n个数,除此之外,你还能想到什么? 师生共同探究等比数列的通项公式,并利用下图获知 活动三 数列鉴赏 三角数列 (2)平方数列 (3)斐波拉契数列 1,1,2,3,5,8,13… 学生反复经历“发现规律——表达规律——揭示规律”的过程,利用字母进行规律的一般化表达,并借助图形表达规律,进一步发展学生的符号意识和几何直观。
三、小结回顾 通过本节课的学习,我们学会了什么? 解决规律问题的方法:特殊 一般 特殊 解决规律问题的步骤:观察 猜想 表达 验证 解决规律问题的思想:数形结合 等差数列,等比数列,三角数和平方数的一般化表达 通过小结,建立起本课的知识结构。
配套练习
一、填空题
如图,用相同的圆点按照一定的规律拼出图形,第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点按照此规律,第幅图中圆点的个数是
(用含的代数式表示).
2.如图,下面是用棋子摆成的“”字,按这样的规律摆下去,摆成第个“”字需要 个棋子(用含的代数式表示);摆成第100个“”字需要 个棋子.
3.一个面积为的长方形纸片,第一次截去一半,第二次截去剩下的一半,如此下去,第10次后剩下的面积是 .
4.观察下列一组算式:,,,,,根据你所发现的规律,猜想第个等式为 .
5.有一列数,,,,,那么第n个数是 .
6.如图所示,下列三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中m= (用含n的式子表示).
二、解答题
7.求的值,可令,
则,因此.
仿照以上推理,请你计算出的值.
8.查阅斐波拉契数列的相关资料,说说生活中的那些斐波拉契现象.
