沪科版九年级数学下册24.5三角形的内切圆 同步练习(含答案)
文档属性
| 名称 | 沪科版九年级数学下册24.5三角形的内切圆 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 870.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-18 11:21:20 | ||
图片预览




文档简介
24.5三角形的内切圆
一、选择题
1.如图,点为的内心,,,,则的面积是
A. B. C.2 D.4
2.如图,等边三角形的边长为,高为,内切圆、外接圆的半径分别为,,则下列结论不正确的是
A. B. C. D.
3.如图,中,内切圆和边、、分别相切于点、、,若,,则的度数是
A. B. C. D.
4.如图,和分别是的外切正三角形和内接正三角形,若的面积为1,则的面积为
A.8 B.6 C.4 D.2
5.如图,为的内心,,,,交于点,则的值为
A. B. C.8 D.
6.如图,点和分别是的内心和外心,若,则的度数为
A. B. C. D.
7.如图,在中,,,,是的内切圆,则的半径为
A.1 B. C.2 D.
8.如图,在中,,于,为的内切圆,设的半径为,的长为,则的值为
A. B. C. D.
9.如图,为内切圆,,延长线交于点,若,,则的长为
A. B.1 C. D.
10.如图,是的内切圆,切点分别相为点、、,设的面积、周长分别为、,的半径为,则下列等式:①;②;③;④,其中成立的是
A.①②③④ B.②③④ C.①③④ D.①②③
二、填空题
11.若方程的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为 .
12.如图所示,三角形中,,,,则它的内切圆半径为 .
13.如图,在中,,其周长为20,是的内切圆,其半径为,则的外接圆直径为 .
14.如图,在中,,是它的内切圆,与,,分别切于点,,,若,则 .
15.如图,在中,交,于点,,与的内切圆相切.若的周长为12,则的最大值为 .
16.如图,内切于正方形,边,上两点,,且是的切线,当的面积为时,则的半径是 .
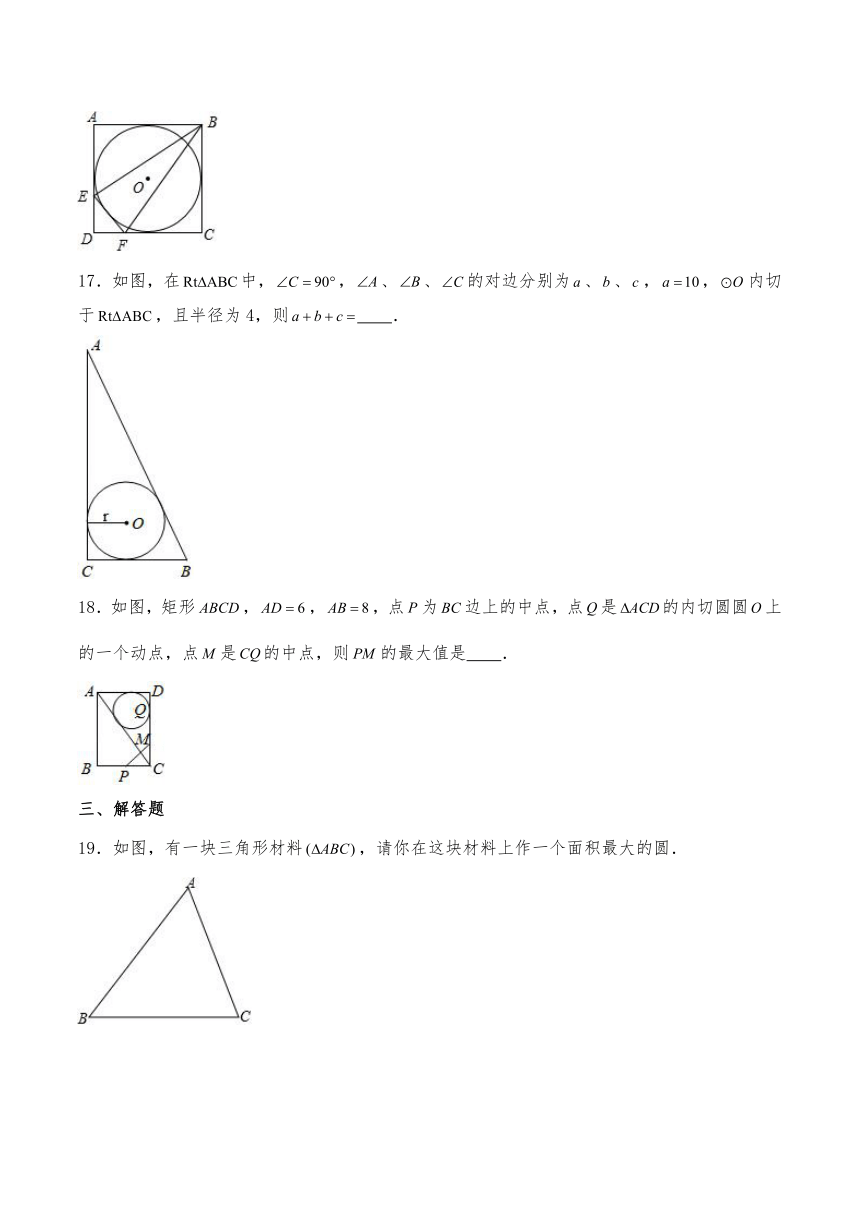
17.如图,在中,,、、的对边分别为、、,,内切于,且半径为4,则 .
18.如图,矩形,,,点为边上的中点,点是的内切圆圆上的一个动点,点是的中点,则的最大值是 .
三、解答题
19.如图,有一块三角形材料,请你在这块材料上作一个面积最大的圆.
20.如图,在的正方形网格中,有部分网格线被擦去.点,,在格点(正方形网格的交点)上.
(1)请用无刻度的直尺在图1中找到三角形的外心;
(2)请用无刻度的直尺在图2中找到三角形的内心.
21.(2020秋 钦州期末)如图,为的内心,连接并延长交的外接圆于点.
求证:.
22.如图,是的外接圆,点是的内心,的延长线交于点,交于点,连接,.
(1)求证:;
(2)若,,求的长.
23.已知:如图,在中,点是的内心(三角形三条角平分线的交点),延长与的外接圆交于点,连接,.
求证:(1);
(2)若,,求的长.
24.如图,点是的内心,的延长线和的外接圆相交于点、过作直线.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的半径.
答案
一、选择题
..........
二、填空题
11.1. 12.. 13.. 14.. 15..
16.. 17.60. 18..
三、解答题
19.分别作,的角平分线,交点即为圆心,再作圆.
如图所示:
20.(1)如图,点即为所求;
(2)如图,点即为所求.
21.证明:如图,连接,
点是的内心,
,,
,
,
,
,,
,
,
;
22.(1)证明:点是的内心,
平分,平分,
,,
又与所对弧为,
.
,,
即,
故.
(2)解:,,
,
①,
,,设,
由(1)可得,
则①式化为,
解得:,(不符题意,舍去),
则.
23.(1)证明:连接,如图1所示:
点是的内心,
平分,
,,
,,,
,
;
(2)解:过点作于,如图2所示:
由(1)得:,
,
,
,
,
,
,
,
,,
.
24.(1)证明:连接交于,如图,
点是的内心
平分,
即,
,
,,
,
,
是的切线;
(2)证明:连接,
点是的内心,
,
,
,
即,
,
,
,
;
(3)解:连接,,如图,
由(1)得,,
,
,
,,
,
在中,,
,解得:,
在中,
,解得:.
一、选择题
1.如图,点为的内心,,,,则的面积是
A. B. C.2 D.4
2.如图,等边三角形的边长为,高为,内切圆、外接圆的半径分别为,,则下列结论不正确的是
A. B. C. D.
3.如图,中,内切圆和边、、分别相切于点、、,若,,则的度数是
A. B. C. D.
4.如图,和分别是的外切正三角形和内接正三角形,若的面积为1,则的面积为
A.8 B.6 C.4 D.2
5.如图,为的内心,,,,交于点,则的值为
A. B. C.8 D.
6.如图,点和分别是的内心和外心,若,则的度数为
A. B. C. D.
7.如图,在中,,,,是的内切圆,则的半径为
A.1 B. C.2 D.
8.如图,在中,,于,为的内切圆,设的半径为,的长为,则的值为
A. B. C. D.
9.如图,为内切圆,,延长线交于点,若,,则的长为
A. B.1 C. D.
10.如图,是的内切圆,切点分别相为点、、,设的面积、周长分别为、,的半径为,则下列等式:①;②;③;④,其中成立的是
A.①②③④ B.②③④ C.①③④ D.①②③
二、填空题
11.若方程的两个根分别是直角三角形两直角边的长,则这个直角三角形的内切圆半径为 .
12.如图所示,三角形中,,,,则它的内切圆半径为 .
13.如图,在中,,其周长为20,是的内切圆,其半径为,则的外接圆直径为 .
14.如图,在中,,是它的内切圆,与,,分别切于点,,,若,则 .
15.如图,在中,交,于点,,与的内切圆相切.若的周长为12,则的最大值为 .
16.如图,内切于正方形,边,上两点,,且是的切线,当的面积为时,则的半径是 .
17.如图,在中,,、、的对边分别为、、,,内切于,且半径为4,则 .
18.如图,矩形,,,点为边上的中点,点是的内切圆圆上的一个动点,点是的中点,则的最大值是 .
三、解答题
19.如图,有一块三角形材料,请你在这块材料上作一个面积最大的圆.
20.如图,在的正方形网格中,有部分网格线被擦去.点,,在格点(正方形网格的交点)上.
(1)请用无刻度的直尺在图1中找到三角形的外心;
(2)请用无刻度的直尺在图2中找到三角形的内心.
21.(2020秋 钦州期末)如图,为的内心,连接并延长交的外接圆于点.
求证:.
22.如图,是的外接圆,点是的内心,的延长线交于点,交于点,连接,.
(1)求证:;
(2)若,,求的长.
23.已知:如图,在中,点是的内心(三角形三条角平分线的交点),延长与的外接圆交于点,连接,.
求证:(1);
(2)若,,求的长.
24.如图,点是的内心,的延长线和的外接圆相交于点、过作直线.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的半径.
答案
一、选择题
..........
二、填空题
11.1. 12.. 13.. 14.. 15..
16.. 17.60. 18..
三、解答题
19.分别作,的角平分线,交点即为圆心,再作圆.
如图所示:
20.(1)如图,点即为所求;
(2)如图,点即为所求.
21.证明:如图,连接,
点是的内心,
,,
,
,
,
,,
,
,
;
22.(1)证明:点是的内心,
平分,平分,
,,
又与所对弧为,
.
,,
即,
故.
(2)解:,,
,
①,
,,设,
由(1)可得,
则①式化为,
解得:,(不符题意,舍去),
则.
23.(1)证明:连接,如图1所示:
点是的内心,
平分,
,,
,,,
,
;
(2)解:过点作于,如图2所示:
由(1)得:,
,
,
,
,
,
,
,
,,
.
24.(1)证明:连接交于,如图,
点是的内心
平分,
即,
,
,,
,
,
是的切线;
(2)证明:连接,
点是的内心,
,
,
,
即,
,
,
,
;
(3)解:连接,,如图,
由(1)得,,
,
,
,,
,
在中,,
,解得:,
在中,
,解得:.
