北师大版八年级数学上册试题 1.1探索勾股定理 同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 1.1探索勾股定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-18 11:44:32 | ||
图片预览




文档简介
1.1《探索勾股定理》
一、选择题
1.已知一个直角三角形三边的平方和为800,则这个直角三角形的斜边长为( )
A.20 B.40 C.80 D.100
2.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为( )
A.7 B.8 C.20 D.65
3.下列各组数据中,是勾股数的是( )
A.3,4,5 B.1,2,3
C.8,9,10 D.5,6,9
4.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
5.如图,,,分别表示以直角三角形三边为边长的正方形面积,则下列结论正确的是( )
A. B. C. D.
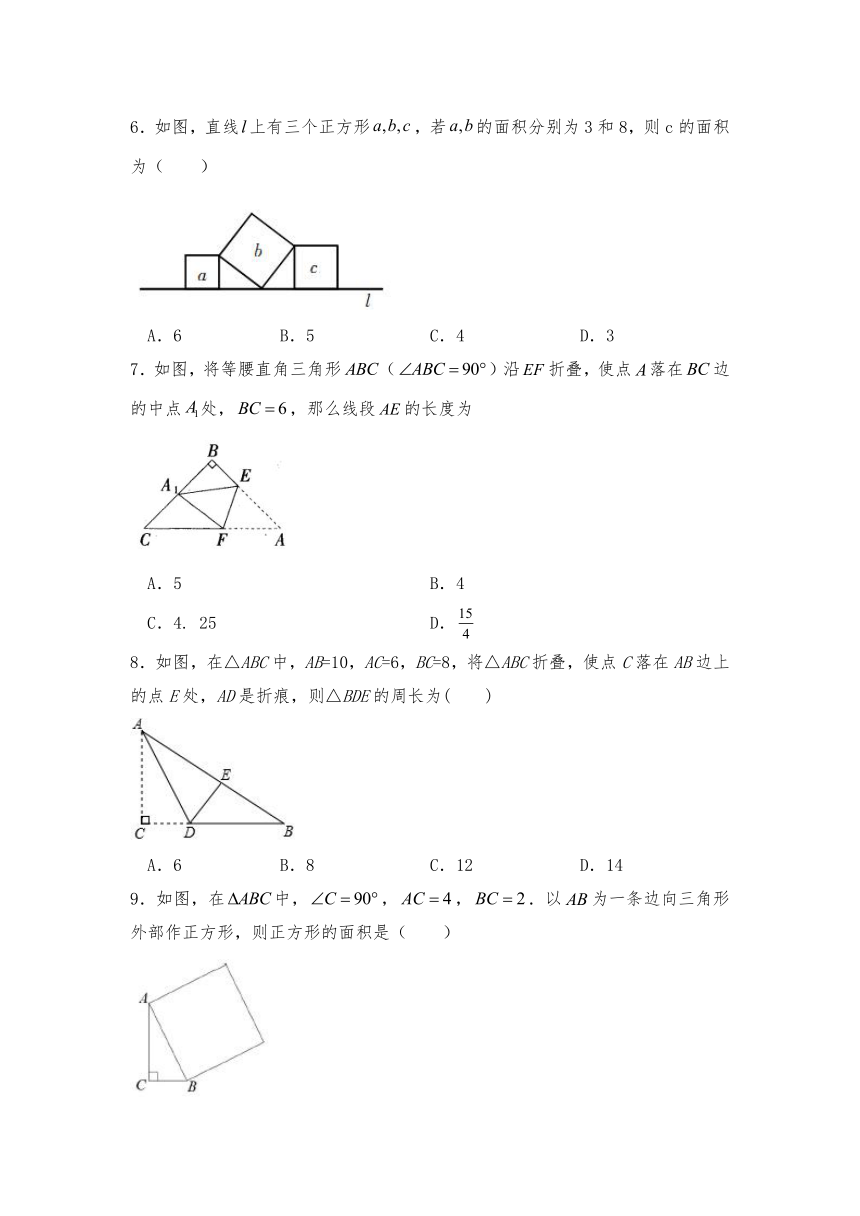
6.如图,直线上有三个正方形,若的面积分别为3和8,则c的面积为( )
A.6 B.5 C.4 D.3
7.如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
A.5 B.4
C.4. 25 D.
8.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为( )
A.6 B.8 C.12 D.14
9.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是( )
A. B. C. D.
10.下列说法正确的是( )
A.若a、b、c是△ABC的三边,则a2b2c2;
B.若a、b、c是Rt△ABC的三边,则a2b2c2;
C.若a、b、c是Rt△ABC的三边,∠A=90°,则a2b2c2;
D.若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2;
11.若△ABC的两边长为4和5,则能使△ABC是直角三角形的第三边的平方是( )
A.9 B.41 C.3 D.9或41
12.在中,、、的对应边分别是a、b、c,若,则下列等式中成立的是( )
A. B. C. D.
二、填空题
1.已知直角三角形的两直角边分别为9和12,则它的周长为______________.
2.一条直角边3,斜边长为5的直角三角的面积为_________.
3.已知甲往东走了3,乙往南走了4,这时甲、乙两人相距____.
4.若15,25,x三个数构成勾股数,则x=___
5.如图,两个较大的正方形面积分别为25,16,那么用字母A代表的正方形面积为___________
6.已知一直角三角形的三边长都是正整数,斜边长13,周长为30,则该直角三角形的面积是________.
7.如图,在Rt△ABC中,∠C=90°,AB=6,则正方形ADEC与正方形BCFG的面积之和为_____.
8.如图,在一次夏令营活动中,小明从营地A出发,沿北偏东53°方向走了400m到达B点,然后再沿北偏西37°方向走了300m到达目的地C.此时A,C两点之间的距离为______m.
三、解答题
1..如图①,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将此图形折叠得图②,折痕为AF,且点C恰好落在边AB上点C′处,求C′F的长.
2.如图,,,,.
(1)请你用无刻度的直尺和圆规,作出的内切圆(保留作图痕迹,不要求写作法);
(2)求的半径长.
3.如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=13cm,BC=12cm,求四边形ABCD的面积.
4.如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边上距直角顶点米远的点处同时开始测量,点为终点.小娟沿的路径测得所经过的路程是米,小燕沿的路径测得所经过的路程也是米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?
5.阅读材料,并解决问题.
有趣的勾股数
定义:勾股数又名毕氏三元数.凡是可以构成一个直角三角形三边长的一组正整数,称之为勾股数.
一般地,若三角形三边长,,都是正整数,且满足,那么数组称为勾股数.公元263年魏朝刘徽著《九章算术注》,文中除提到勾股数以外,还提到,,,等勾股数.
数学小组的同学研究勾股数时发现:设,是两个正整数,且,三角形三边长,,都是正整数.下表中的,,可以组成一些有规律的勾股数.
2 1 3 4 5
3 2 5 12 13
4 1 15 8 17
4 3 7 24 25
5 2 21 20 29
5 4 9 40 41
6 1 35 12 37
6 5 11 60 61
7 2 45 28 53
7 4 33 56 65
7 6 13 84 85
通过观察这个表格中的数据,小明发现勾股数可以写成.解答下列问题:
(1)表中可以用,的代数式表示为_____________.
(2)若,,则勾股数为______________.
(3)小明通过研究表中数据发现:若,则勾股数的形式可表述为(为正整数),请你通过计算求此时的.(用含的代数式表示)
答案
一、选择题
A.B.A.D.D.B.D.C.D.D.D.C.
二、填空题
1.36.
2.6.
3.5.
4.20.
5.9 .
6.30.
32.36
7.36.
33.500
8.500m.
三、解答题
1.解:由折叠得:AC'=AC=6,C'F⊥AB,CF=C'F,
在Rt△ABC中,∠C=90°,BC=8,AC=6,
∴AB=10,
∴BC'=10﹣6=4,
在Rt△BC'F中,设C'F=x,则BF=8﹣x,
∴x2+42=(8﹣x)2,
解方程得:x=3.
即C'F=3.
2.解:(1)如图所示,
(2)过作于点,于点,
∴,,
又∵,
∴四边形是矩形(有三个角是直角的四边形是矩形)
∵,
∴矩形是正方形,
∴,
设的半径为,则,
∵是的内切圆,
∴,(从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角)
∵中,,,,
∴,
∴,
∴.
答:圆的半径长为2.
3.解:连接BD,
AB⊥AD,
,
在中,
在中,,
是直角三角形,
4.解:中,,
设,,
则.
,
又在中,由勾股定理得:,
,
解得:,即(米)
米,米,米
×5×12=×13h,米
答:这个直角三角花台底边上的高位为米
5.解:(1)∵4=2×2×1,
12=2×3×2,
8=2×4×1,
24=2×4×3,
…,
∴,
故答案为:;
(2)当,时,
a=m2-n2=42-22=12,=2×4×2=16,c=m2+n2=42+22=20,
∴勾股数为,
故答案为:;
(3)根据题意,得,
∴,
解得.
一、选择题
1.已知一个直角三角形三边的平方和为800,则这个直角三角形的斜边长为( )
A.20 B.40 C.80 D.100
2.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为( )
A.7 B.8 C.20 D.65
3.下列各组数据中,是勾股数的是( )
A.3,4,5 B.1,2,3
C.8,9,10 D.5,6,9
4.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
5.如图,,,分别表示以直角三角形三边为边长的正方形面积,则下列结论正确的是( )
A. B. C. D.
6.如图,直线上有三个正方形,若的面积分别为3和8,则c的面积为( )
A.6 B.5 C.4 D.3
7.如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
A.5 B.4
C.4. 25 D.
8.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为( )
A.6 B.8 C.12 D.14
9.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是( )
A. B. C. D.
10.下列说法正确的是( )
A.若a、b、c是△ABC的三边,则a2b2c2;
B.若a、b、c是Rt△ABC的三边,则a2b2c2;
C.若a、b、c是Rt△ABC的三边,∠A=90°,则a2b2c2;
D.若a、b、c是Rt△ABC的三边,∠C=90°,则a2b2c2;
11.若△ABC的两边长为4和5,则能使△ABC是直角三角形的第三边的平方是( )
A.9 B.41 C.3 D.9或41
12.在中,、、的对应边分别是a、b、c,若,则下列等式中成立的是( )
A. B. C. D.
二、填空题
1.已知直角三角形的两直角边分别为9和12,则它的周长为______________.
2.一条直角边3,斜边长为5的直角三角的面积为_________.
3.已知甲往东走了3,乙往南走了4,这时甲、乙两人相距____.
4.若15,25,x三个数构成勾股数,则x=___
5.如图,两个较大的正方形面积分别为25,16,那么用字母A代表的正方形面积为___________
6.已知一直角三角形的三边长都是正整数,斜边长13,周长为30,则该直角三角形的面积是________.
7.如图,在Rt△ABC中,∠C=90°,AB=6,则正方形ADEC与正方形BCFG的面积之和为_____.
8.如图,在一次夏令营活动中,小明从营地A出发,沿北偏东53°方向走了400m到达B点,然后再沿北偏西37°方向走了300m到达目的地C.此时A,C两点之间的距离为______m.
三、解答题
1..如图①,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将此图形折叠得图②,折痕为AF,且点C恰好落在边AB上点C′处,求C′F的长.
2.如图,,,,.
(1)请你用无刻度的直尺和圆规,作出的内切圆(保留作图痕迹,不要求写作法);
(2)求的半径长.
3.如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=13cm,BC=12cm,求四边形ABCD的面积.
4.如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边上距直角顶点米远的点处同时开始测量,点为终点.小娟沿的路径测得所经过的路程是米,小燕沿的路径测得所经过的路程也是米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?
5.阅读材料,并解决问题.
有趣的勾股数
定义:勾股数又名毕氏三元数.凡是可以构成一个直角三角形三边长的一组正整数,称之为勾股数.
一般地,若三角形三边长,,都是正整数,且满足,那么数组称为勾股数.公元263年魏朝刘徽著《九章算术注》,文中除提到勾股数以外,还提到,,,等勾股数.
数学小组的同学研究勾股数时发现:设,是两个正整数,且,三角形三边长,,都是正整数.下表中的,,可以组成一些有规律的勾股数.
2 1 3 4 5
3 2 5 12 13
4 1 15 8 17
4 3 7 24 25
5 2 21 20 29
5 4 9 40 41
6 1 35 12 37
6 5 11 60 61
7 2 45 28 53
7 4 33 56 65
7 6 13 84 85
通过观察这个表格中的数据,小明发现勾股数可以写成.解答下列问题:
(1)表中可以用,的代数式表示为_____________.
(2)若,,则勾股数为______________.
(3)小明通过研究表中数据发现:若,则勾股数的形式可表述为(为正整数),请你通过计算求此时的.(用含的代数式表示)
答案
一、选择题
A.B.A.D.D.B.D.C.D.D.D.C.
二、填空题
1.36.
2.6.
3.5.
4.20.
5.9 .
6.30.
32.36
7.36.
33.500
8.500m.
三、解答题
1.解:由折叠得:AC'=AC=6,C'F⊥AB,CF=C'F,
在Rt△ABC中,∠C=90°,BC=8,AC=6,
∴AB=10,
∴BC'=10﹣6=4,
在Rt△BC'F中,设C'F=x,则BF=8﹣x,
∴x2+42=(8﹣x)2,
解方程得:x=3.
即C'F=3.
2.解:(1)如图所示,
(2)过作于点,于点,
∴,,
又∵,
∴四边形是矩形(有三个角是直角的四边形是矩形)
∵,
∴矩形是正方形,
∴,
设的半径为,则,
∵是的内切圆,
∴,(从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角)
∵中,,,,
∴,
∴,
∴.
答:圆的半径长为2.
3.解:连接BD,
AB⊥AD,
,
在中,
在中,,
是直角三角形,
4.解:中,,
设,,
则.
,
又在中,由勾股定理得:,
,
解得:,即(米)
米,米,米
×5×12=×13h,米
答:这个直角三角花台底边上的高位为米
5.解:(1)∵4=2×2×1,
12=2×3×2,
8=2×4×1,
24=2×4×3,
…,
∴,
故答案为:;
(2)当,时,
a=m2-n2=42-22=12,=2×4×2=16,c=m2+n2=42+22=20,
∴勾股数为,
故答案为:;
(3)根据题意,得,
∴,
解得.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
