第一章集合与常用逻辑 章末复习 课件(共27张PPT)
文档属性
| 名称 | 第一章集合与常用逻辑 章末复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 956.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-17 10:07:12 | ||
图片预览








文档简介
(共27张PPT)
第一章 集合与常用逻辑
章末复习
教学目标
1.回顾本章基本知识,构建本章知识网络结构;
2.掌握基本题型和数学思想方法.
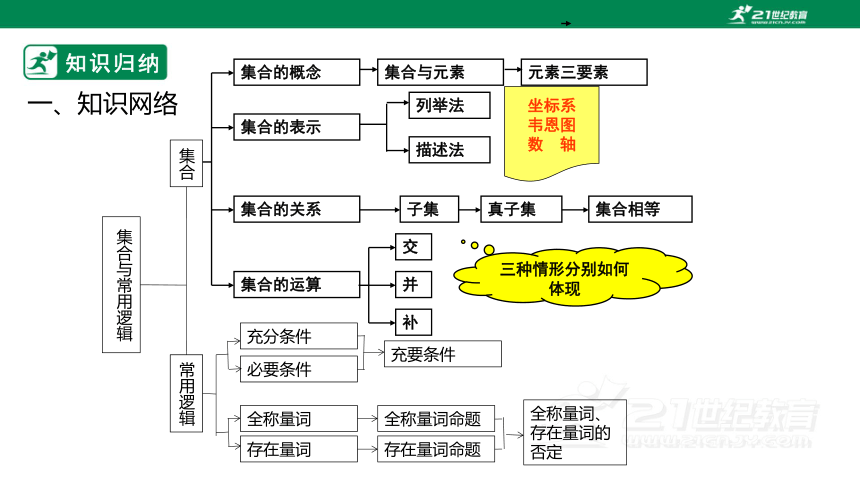
知识归纳
集合与常用逻辑
坐标系
韦恩图
数 轴
列举法
描述法
子集
真子集
集合相等
交
并
补
三种情形分别如何体现
集合的运算
集合的关系
集合的表示
集合的概念
集合与元素
元素三要素
集合
全称量词、存在量词的否定
充要条件
常用逻辑
充分条件
必要条件
全称量词
存在量词
全称量词命题
存在量词命题
一、知识网络
知识归纳
二、知识回顾
1.元素与集合
(1)集合元素的三大特性:
⑴集合的三大特性:
⑵元素与集合的关系:
⑶集合的表示方法:
属于(a∈A)或不属于(b A).
确定性、互异性、无序性.
列举法、描述法、韦恩图(venn)或数轴.
知识归纳
二、知识回顾
2.集合间的基本关系
(1)集合元素的三大特性:
⑴子集:对于 x∈A,都有x∈B ,则A B(或B A).
⑵真子集:若A B,且B中至少有一个元素不属于A,则A B.
⑶集合相等:若A B,且B A,则A=B.
⑷空集性质: 是任何集合的子集,是任何非空集合的真子集.
知识归纳
二、知识回顾
3.集合的运算
(1)集合元素的三大特性:
⑴并集:A∪B={x|x∈A或x∈B}
性质:A∪B=B∪A,A A∪B,B A∪B,A∪A=A,A∪ =A
若A∪B=B,则A B.
⑵交集:A∩B={x|x∈A且x∈B}
性质:A∩B=B∩A,A∩B A,A∩B B,A∩A=A,A∩ =
若A∩B=B,则B A.
⑶全集与并集:设A U,则CUA={x|x∈U且x A}
性质:A∪CUA=U,A∩CUA= ,CU(CUA)=A
知识归纳
二、知识回顾
4.充分条件与必要条件
(1)集合元素的三大特性:
⑴若p q,则p是q的充分条件,q是p的必要条件;
⑵若p q,且q p,则p是q的充分不必要条件;
⑶若p q,且q p,则p是q的必要不充分条件;
⑷若p q,且q p,则p是q的充分必要条件;(充要条件)
⑸若p q,且q p,则p是q的既充分也不必要条件.
知识归纳
二、知识回顾
5.全称量词命题与存在量词命题的否定
(1)集合元素的三大特性:
⑴全称量词命题及其否定
全称量词命题:对M中任意的一个x,有p(x)成立.
数学语言: x∈M,p(x).
全称量词命题的否定: x∈M, p(x)
⑵存在量词命题及其否定
存在量词命题:存在M中的元素x,有p(x)成立.
数学语言: x∈M,p(x).
存在量词命题的否定: x∈M, p(x)
知识归纳
三、思想方法
(1)集合元素的三大特性:
⑴转化化归思想
⑵逆向思维思想(补集思想)
⑶分类讨论思想
⑷数形结合思想
考点讲析
考点1:集合的概念
1.(多选)非空集合A具有下列性质:①若x,y∈A,则 ∈A;②若x,y∈A,则x+y∈A.
下列选项正确的是( )
A.-1 A B.若x,y∈A,则xy∈A
C. A D.若x,y∈A,则x-y A
2.同时满足:①M {1,2,3,4,5},②a∈M,则6-a∈M的非空集合M有( )
A.6个 B.7个 C.15个 D.16个
3.若-1∈{a-1,2a+1,a2-1},则实数a的取值的集合为 .
4.已知集合A={(x,y)|x2+y2≤3,x∈z,y∈z},则A中元素的个数为 .
考点讲析
【答案】1.AB
2.7个 简析:符合条件的M集合分别{3},{1,3},{2,4},
{1,3,5},{2,3,4},{1,2,4,5},{1,2,3,4,5}.
3.{-1}
4.9个.
考点讲析
考点2:集合之间的关系
1.集合{y∈N|y=-x2+6,x∈N}的真子集的个数为 .
2.已知集合M={x|x2+x-2=0},P={x|ax+1=0},且P M,则实数a的值的集合为 .
3.已知集合A={x∈R|2a≤x≤a+3},B={x∈R|x<-1或x>4},若A B,则实数a的取值范围
是 .
考点讲析
【答案】1.7个 简析:{y∈N|y=-x2+6,x∈N}={2,5,6},他的真子集个数为22-1=7
2.{0,-1, }
3.{a|a<-4或2考点讲析
考点3:集合的基本运算
1.设全集U={1,2,3,4,5},集合M满足CUM={1,3},则( )
A.2∈M B.3∈M C.4 M D.5 M
2.已知全集U=R,集合M={x|x<1},N={x|-1A.CU(M∪N) B.N∪CUM C.CU(M∩N) D.M∪CUN
3.已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T=( )
A. B.S C.T D.Z
4.已知集合M={-2,-1,0,1,2},N={x|x2-x-6≥0},则M N=( )
A.{-2,-1,0,1} B. {0,1,2} C.{-2} D.{2}
5.已知集合A={x∈R|x<-6或x>3},B={x∈R|a≤x≤a+1},若A B≠ ,求实数a的
取值范围.
考点讲析
【答案】1.A
2.A 简析:M∪N={x|x<2},则{x|x≥2}=CU(M∪N),故选A
3.T
4.C
5.{a|a<-6或a>2}=(-∞,-6)∪(2,+∞)
考点讲析
考点4:充分条件、必要条件及应用
1.“x>2”是“x2-x-2>0”的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
2.“关于x的不等式x2-x+m>0在R上恒成立”的充要条件是( )
A.m> B.m< C.m<1 D.m>1
3.若p:x2+x-6=0是q:ax+1=0的必要不充分条件,求实数a的值.
4.设命题p:x2-3x+2<0,命题q:(x-a)(x-1)≤0,若p是q的充分不必要条件,求实数a的取值范围.
考点讲析
【答案】1.A
2.A 3.a=- 或a=
4.a>2
考点讲析
考点5:全称量词命题与存在量词命题
1.(多选)下列结论正确的是( )
A.命题“所以四边形都是矩形”是存在量词命题;
B.命题“ x∈R,x2+3>0”是全称量词命题;
C.若p: x∈R,x2+4x+4≤0,则 p: x∈R,x2+4x+4>0;
D.命题“有些实数的绝对值是正数”的否定是 x∈R,|x|<0.
2.命题“ x∈N,x2≥2x+1”的否定是( )
A. x N,x2<2x+1 B. x∈N,x2<2x+1
C. x N,x2<2x+1 D. x∈N,x2<2x+1
3.设非空集合P,Q,满足P∩Q=P,则( )
A. x∈Q,有x∈P B. x Q,有x P
C. x Q,使得x∈P D. x∈Q,使得x P
4.设函数f(x)=mx2-mx-1,命题“ x∈[1,3],f(x)≤-m+2”是假命题,则实数m的取值范围为 .
考点讲析
【答案】1.BC
2.B 3.A
4.m>3
初试身手
1.(多选)设集合M={x|(x-a)(x-1)=0},P={1,4},则M∪P的子集个数可能为( )
A.2 B. 4 C.8 D.16
2.已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B=( )
A.{-1,2} B.{1,2} C.{1,4} D.{-1,4}
3.已知全集U={0,2,4,6,8,10},A={4,8},则CUA=( )
A.{4,8} B.{0,2,6} C.{0,2,6,10} D.{0,2,4,6,8,10}
4.若不等式|x-1|5.已知命题p: x∈R, x2+(a-1)x+1<0,若命题p为假命题,则a的取值范围是( )
A.1≤a≤3 B.-16.已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
⑴若(CRA)∪B=R,求a的取值范围;
⑵是否存在a,使(CRA)∪B=R且A∩B= 若存在,求a的值;若不存在,说明理由.
考点讲析
【答案】1.BC
2.B 3.C
4.a≥3 5.C
6.⑴-1≤a≤0 ⑵不存在.
解析:(1)A={x|0≤x≤2},
∴CRA={x|x<0或x>2}.
∵(CRA)∪B=R,
∴
∴-1≤a≤0.
(2)由(1)知(CRA)∪B=R时,-1≤a≤0,而2≤a+3≤3,
∴A B,这与A∩B= 矛盾.即这样的a不存在.
初试身手
作业:p34-35 复习参考题1第2,4,6,7,9题
尽情享受学习数学的快乐!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 集合与常用逻辑
章末复习
教学目标
1.回顾本章基本知识,构建本章知识网络结构;
2.掌握基本题型和数学思想方法.
知识归纳
集合与常用逻辑
坐标系
韦恩图
数 轴
列举法
描述法
子集
真子集
集合相等
交
并
补
三种情形分别如何体现
集合的运算
集合的关系
集合的表示
集合的概念
集合与元素
元素三要素
集合
全称量词、存在量词的否定
充要条件
常用逻辑
充分条件
必要条件
全称量词
存在量词
全称量词命题
存在量词命题
一、知识网络
知识归纳
二、知识回顾
1.元素与集合
(1)集合元素的三大特性:
⑴集合的三大特性:
⑵元素与集合的关系:
⑶集合的表示方法:
属于(a∈A)或不属于(b A).
确定性、互异性、无序性.
列举法、描述法、韦恩图(venn)或数轴.
知识归纳
二、知识回顾
2.集合间的基本关系
(1)集合元素的三大特性:
⑴子集:对于 x∈A,都有x∈B ,则A B(或B A).
⑵真子集:若A B,且B中至少有一个元素不属于A,则A B.
⑶集合相等:若A B,且B A,则A=B.
⑷空集性质: 是任何集合的子集,是任何非空集合的真子集.
知识归纳
二、知识回顾
3.集合的运算
(1)集合元素的三大特性:
⑴并集:A∪B={x|x∈A或x∈B}
性质:A∪B=B∪A,A A∪B,B A∪B,A∪A=A,A∪ =A
若A∪B=B,则A B.
⑵交集:A∩B={x|x∈A且x∈B}
性质:A∩B=B∩A,A∩B A,A∩B B,A∩A=A,A∩ =
若A∩B=B,则B A.
⑶全集与并集:设A U,则CUA={x|x∈U且x A}
性质:A∪CUA=U,A∩CUA= ,CU(CUA)=A
知识归纳
二、知识回顾
4.充分条件与必要条件
(1)集合元素的三大特性:
⑴若p q,则p是q的充分条件,q是p的必要条件;
⑵若p q,且q p,则p是q的充分不必要条件;
⑶若p q,且q p,则p是q的必要不充分条件;
⑷若p q,且q p,则p是q的充分必要条件;(充要条件)
⑸若p q,且q p,则p是q的既充分也不必要条件.
知识归纳
二、知识回顾
5.全称量词命题与存在量词命题的否定
(1)集合元素的三大特性:
⑴全称量词命题及其否定
全称量词命题:对M中任意的一个x,有p(x)成立.
数学语言: x∈M,p(x).
全称量词命题的否定: x∈M, p(x)
⑵存在量词命题及其否定
存在量词命题:存在M中的元素x,有p(x)成立.
数学语言: x∈M,p(x).
存在量词命题的否定: x∈M, p(x)
知识归纳
三、思想方法
(1)集合元素的三大特性:
⑴转化化归思想
⑵逆向思维思想(补集思想)
⑶分类讨论思想
⑷数形结合思想
考点讲析
考点1:集合的概念
1.(多选)非空集合A具有下列性质:①若x,y∈A,则 ∈A;②若x,y∈A,则x+y∈A.
下列选项正确的是( )
A.-1 A B.若x,y∈A,则xy∈A
C. A D.若x,y∈A,则x-y A
2.同时满足:①M {1,2,3,4,5},②a∈M,则6-a∈M的非空集合M有( )
A.6个 B.7个 C.15个 D.16个
3.若-1∈{a-1,2a+1,a2-1},则实数a的取值的集合为 .
4.已知集合A={(x,y)|x2+y2≤3,x∈z,y∈z},则A中元素的个数为 .
考点讲析
【答案】1.AB
2.7个 简析:符合条件的M集合分别{3},{1,3},{2,4},
{1,3,5},{2,3,4},{1,2,4,5},{1,2,3,4,5}.
3.{-1}
4.9个.
考点讲析
考点2:集合之间的关系
1.集合{y∈N|y=-x2+6,x∈N}的真子集的个数为 .
2.已知集合M={x|x2+x-2=0},P={x|ax+1=0},且P M,则实数a的值的集合为 .
3.已知集合A={x∈R|2a≤x≤a+3},B={x∈R|x<-1或x>4},若A B,则实数a的取值范围
是 .
考点讲析
【答案】1.7个 简析:{y∈N|y=-x2+6,x∈N}={2,5,6},他的真子集个数为22-1=7
2.{0,-1, }
3.{a|a<-4或2
考点3:集合的基本运算
1.设全集U={1,2,3,4,5},集合M满足CUM={1,3},则( )
A.2∈M B.3∈M C.4 M D.5 M
2.已知全集U=R,集合M={x|x<1},N={x|-1
3.已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T=( )
A. B.S C.T D.Z
4.已知集合M={-2,-1,0,1,2},N={x|x2-x-6≥0},则M N=( )
A.{-2,-1,0,1} B. {0,1,2} C.{-2} D.{2}
5.已知集合A={x∈R|x<-6或x>3},B={x∈R|a≤x≤a+1},若A B≠ ,求实数a的
取值范围.
考点讲析
【答案】1.A
2.A 简析:M∪N={x|x<2},则{x|x≥2}=CU(M∪N),故选A
3.T
4.C
5.{a|a<-6或a>2}=(-∞,-6)∪(2,+∞)
考点讲析
考点4:充分条件、必要条件及应用
1.“x>2”是“x2-x-2>0”的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
2.“关于x的不等式x2-x+m>0在R上恒成立”的充要条件是( )
A.m> B.m< C.m<1 D.m>1
3.若p:x2+x-6=0是q:ax+1=0的必要不充分条件,求实数a的值.
4.设命题p:x2-3x+2<0,命题q:(x-a)(x-1)≤0,若p是q的充分不必要条件,求实数a的取值范围.
考点讲析
【答案】1.A
2.A 3.a=- 或a=
4.a>2
考点讲析
考点5:全称量词命题与存在量词命题
1.(多选)下列结论正确的是( )
A.命题“所以四边形都是矩形”是存在量词命题;
B.命题“ x∈R,x2+3>0”是全称量词命题;
C.若p: x∈R,x2+4x+4≤0,则 p: x∈R,x2+4x+4>0;
D.命题“有些实数的绝对值是正数”的否定是 x∈R,|x|<0.
2.命题“ x∈N,x2≥2x+1”的否定是( )
A. x N,x2<2x+1 B. x∈N,x2<2x+1
C. x N,x2<2x+1 D. x∈N,x2<2x+1
3.设非空集合P,Q,满足P∩Q=P,则( )
A. x∈Q,有x∈P B. x Q,有x P
C. x Q,使得x∈P D. x∈Q,使得x P
4.设函数f(x)=mx2-mx-1,命题“ x∈[1,3],f(x)≤-m+2”是假命题,则实数m的取值范围为 .
考点讲析
【答案】1.BC
2.B 3.A
4.m>3
初试身手
1.(多选)设集合M={x|(x-a)(x-1)=0},P={1,4},则M∪P的子集个数可能为( )
A.2 B. 4 C.8 D.16
2.已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B=( )
A.{-1,2} B.{1,2} C.{1,4} D.{-1,4}
3.已知全集U={0,2,4,6,8,10},A={4,8},则CUA=( )
A.{4,8} B.{0,2,6} C.{0,2,6,10} D.{0,2,4,6,8,10}
4.若不等式|x-1|
A.1≤a≤3 B.-1
⑴若(CRA)∪B=R,求a的取值范围;
⑵是否存在a,使(CRA)∪B=R且A∩B= 若存在,求a的值;若不存在,说明理由.
考点讲析
【答案】1.BC
2.B 3.C
4.a≥3 5.C
6.⑴-1≤a≤0 ⑵不存在.
解析:(1)A={x|0≤x≤2},
∴CRA={x|x<0或x>2}.
∵(CRA)∪B=R,
∴
∴-1≤a≤0.
(2)由(1)知(CRA)∪B=R时,-1≤a≤0,而2≤a+3≤3,
∴A B,这与A∩B= 矛盾.即这样的a不存在.
初试身手
作业:p34-35 复习参考题1第2,4,6,7,9题
尽情享受学习数学的快乐!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
