二次函数及图象
图片预览

文档简介
第二讲 二次函数及图象
一、知识归纳
1、二次函数的概念: 一般地,如果y=ax2+bx+c(a,b,c是常数且a≠0),那么y叫做x的二次函数,
一般式:y=ax2+bx+c,通常要知道图像上的三个点的坐标
顶点式:y=a(x-h)2+k,通常要知道顶点坐标或对称轴
交点式:y=a(x-x1)(x-x2),要知道图像与x轴的两个交点坐标x1,x2
2、二次函数的图像: 抛物线三要素:开口方向,对称轴,顶点.
当时,抛物线开口向上,对称轴为,顶点坐标为.有最小值.
当时,抛物线开口向下,对称轴为,顶点坐标为.有最大值.
若y=a(x-h)2+k,顶点坐标为(h,k),对称轴x=h
(1)决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小.
(2) 在确定的前提下,决定了抛物线对称轴的位置.概括的说就是“左同右异”
对称轴在轴左边,,在轴的右侧,
(3) c决定了抛物线与轴交点的位置.
3、二次函数图象的平移:图象的平移实质是顶点的平移
例题讲解
例1:函数 的开口 ,顶点坐标是 ,对称轴是 .
当x 时.y随x的增大而减小。当x 时.y有最 值为
把这个函数向左平移2个单位,向下平移3个单位得到的函数解析式为 。
例2:(1) 二次函数y=ax2+bx+c的图象如图所示,下列各不等式中成立的是____________
①abc<0 ②a+b+c < 0 ③a+c > b
④2a+b=0 ⑤b2-4ac >0
(2)若(-2,y1),(-2.5, y2)是抛物线y=-(x+1)2+4的两点,
则 y1 y2(填>,<或=)
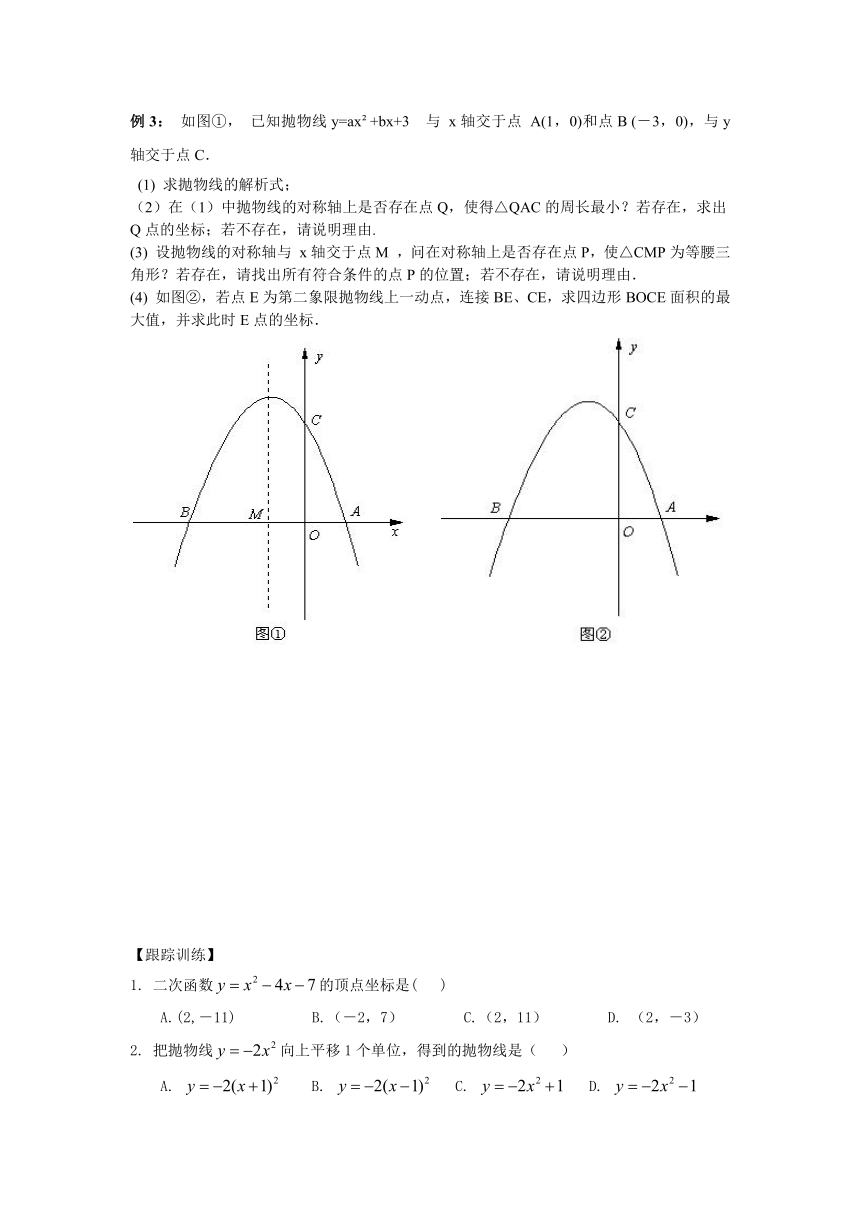
例3: 如图①, 已知抛物线y=ax +bx+3 与 x轴交于点 A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3) 设抛物线的对称轴与 x轴交于点M ( http: / / www.21cnjy.com ) ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请找出所有符合条件的点P的位置;若不存在,请说明理由.
(4) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
【跟踪训练】
1. 二次函数的顶点坐标是( )
A.(2,-11) B.(-2,7) C.(2,11) D. (2,-3)
2. 把抛物线向上平移1个单位,得到的抛物线是( )
A. B. C. D.
3. 已知二次函数y=2(x﹣3)2+1.下列说法:
①其图象的开口向下;②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
4.已知A(-4,y1),B(-3,y2) ( http: / / www.21cnjy.com ),C(1,y3)为二次函数 y=x2+4x-5的图象的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y1<y3<y2
5.二次函数y=ax2+bx+c的图象如图所示,它与x轴的
两个交点分别为(﹣1,0),(3,0).对于下列命题:
①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.
其中正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
6.二次函数的对称轴是,则_______。
7.抛物线的顶点为C,直线过点C,则这条直线与两坐标轴所围成的三角形面积为 。
8.已知:二次函数为y=x2-x+m,
写出它的图像的开口方向,对称轴及顶点坐标;
m为何值时,顶点在x轴上方,
若抛物线与y轴交于A,过A作AB∥x轴交抛物线于另一点B,当S△AOB=4时,求此二次函数的解析式.
课堂检测:
1.下列抛物线的顶点坐标为(0,1)的是( )
A.y=x2+1 B.y=x2-1 C.y=(x+1)2 D.y=(x-1)2
2.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
A.与x轴有两个交点 B.开口向上
C.与y轴的交点坐标是(0,3) D.顶点坐标是(1,-2)
3.二次函数y=-x2+2x的图象可能是( )
4.如图,直角坐标系中,两条抛物线有相同的对称轴,
下列关系不正确的是( )
A. B.
C. D.
5.已知二次函数y=ax2+bx+c(a<0)的图象如图,
当-5≤x≤0时,下列说法正确的是( )
A.有最小值-5、最大值0
B.有最小值-3、最大值6
C.有最小值0、最大值6
D.有最小值2、最大值6
6.若函数y=(m-3)是二次函数,则m=______.
7.二次函数的图象是由的图象向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
8.已知,如图抛物线y=ax2+3ax+c ( http: / / www.21cnjy.com )(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P ( http: / / www.21cnjy.com )在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
y
1
-1
0
x
一、知识归纳
1、二次函数的概念: 一般地,如果y=ax2+bx+c(a,b,c是常数且a≠0),那么y叫做x的二次函数,
一般式:y=ax2+bx+c,通常要知道图像上的三个点的坐标
顶点式:y=a(x-h)2+k,通常要知道顶点坐标或对称轴
交点式:y=a(x-x1)(x-x2),要知道图像与x轴的两个交点坐标x1,x2
2、二次函数的图像: 抛物线三要素:开口方向,对称轴,顶点.
当时,抛物线开口向上,对称轴为,顶点坐标为.有最小值.
当时,抛物线开口向下,对称轴为,顶点坐标为.有最大值.
若y=a(x-h)2+k,顶点坐标为(h,k),对称轴x=h
(1)决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小.
(2) 在确定的前提下,决定了抛物线对称轴的位置.概括的说就是“左同右异”
对称轴在轴左边,,在轴的右侧,
(3) c决定了抛物线与轴交点的位置.
3、二次函数图象的平移:图象的平移实质是顶点的平移
例题讲解
例1:函数 的开口 ,顶点坐标是 ,对称轴是 .
当x 时.y随x的增大而减小。当x 时.y有最 值为
把这个函数向左平移2个单位,向下平移3个单位得到的函数解析式为 。
例2:(1) 二次函数y=ax2+bx+c的图象如图所示,下列各不等式中成立的是____________
①abc<0 ②a+b+c < 0 ③a+c > b
④2a+b=0 ⑤b2-4ac >0
(2)若(-2,y1),(-2.5, y2)是抛物线y=-(x+1)2+4的两点,
则 y1 y2(填>,<或=)
例3: 如图①, 已知抛物线y=ax +bx+3 与 x轴交于点 A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3) 设抛物线的对称轴与 x轴交于点M ( http: / / www.21cnjy.com ) ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请找出所有符合条件的点P的位置;若不存在,请说明理由.
(4) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
【跟踪训练】
1. 二次函数的顶点坐标是( )
A.(2,-11) B.(-2,7) C.(2,11) D. (2,-3)
2. 把抛物线向上平移1个单位,得到的抛物线是( )
A. B. C. D.
3. 已知二次函数y=2(x﹣3)2+1.下列说法:
①其图象的开口向下;②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
4.已知A(-4,y1),B(-3,y2) ( http: / / www.21cnjy.com ),C(1,y3)为二次函数 y=x2+4x-5的图象的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y1<y3<y2
5.二次函数y=ax2+bx+c的图象如图所示,它与x轴的
两个交点分别为(﹣1,0),(3,0).对于下列命题:
①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.
其中正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
6.二次函数的对称轴是,则_______。
7.抛物线的顶点为C,直线过点C,则这条直线与两坐标轴所围成的三角形面积为 。
8.已知:二次函数为y=x2-x+m,
写出它的图像的开口方向,对称轴及顶点坐标;
m为何值时,顶点在x轴上方,
若抛物线与y轴交于A,过A作AB∥x轴交抛物线于另一点B,当S△AOB=4时,求此二次函数的解析式.
课堂检测:
1.下列抛物线的顶点坐标为(0,1)的是( )
A.y=x2+1 B.y=x2-1 C.y=(x+1)2 D.y=(x-1)2
2.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
A.与x轴有两个交点 B.开口向上
C.与y轴的交点坐标是(0,3) D.顶点坐标是(1,-2)
3.二次函数y=-x2+2x的图象可能是( )
4.如图,直角坐标系中,两条抛物线有相同的对称轴,
下列关系不正确的是( )
A. B.
C. D.
5.已知二次函数y=ax2+bx+c(a<0)的图象如图,
当-5≤x≤0时,下列说法正确的是( )
A.有最小值-5、最大值0
B.有最小值-3、最大值6
C.有最小值0、最大值6
D.有最小值2、最大值6
6.若函数y=(m-3)是二次函数,则m=______.
7.二次函数的图象是由的图象向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。
8.已知,如图抛物线y=ax2+3ax+c ( http: / / www.21cnjy.com )(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P ( http: / / www.21cnjy.com )在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
y
1
-1
0
x
同课章节目录
