9.2.2总体百分位数的估计 课件(共21张PPT)
文档属性
| 名称 | 9.2.2总体百分位数的估计 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 12:23:10 | ||
图片预览






文档简介
(共21张PPT)
9.2.2总体百分数的估计
创设情境
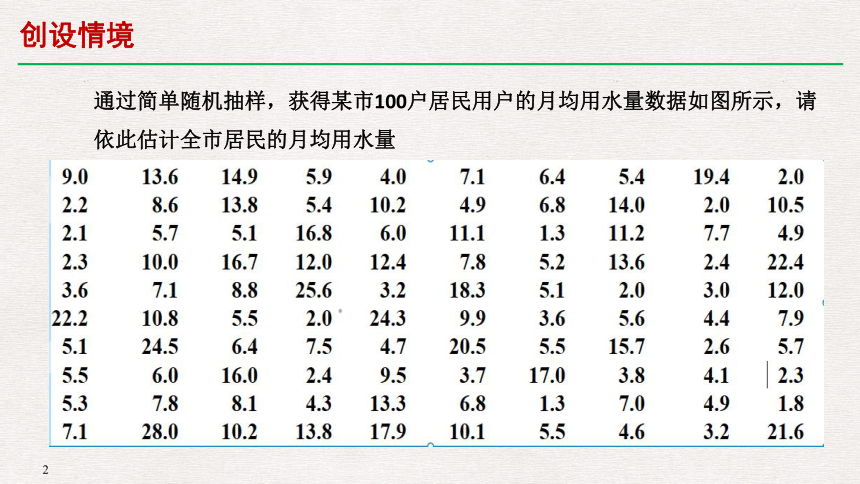
通过简单随机抽样,获得某市100户居民用户的月均用水量数据如图所示,请依此估计全市居民的月均用水量
问题引导
问题2 如果市政府希望使的居民用户生活用水费支出不受影响,根据这户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
分析:根据市政府的要求确定居民用户月均用水量标准,就是要寻找一个数,使得全市居民用户月均用水量不超过的占大于的占.
80%
20%
50%
50%
a
a
中位数(第50百分位数,50%分位数)
第80百分位数(80%分位数)
类比抽象,探究新知
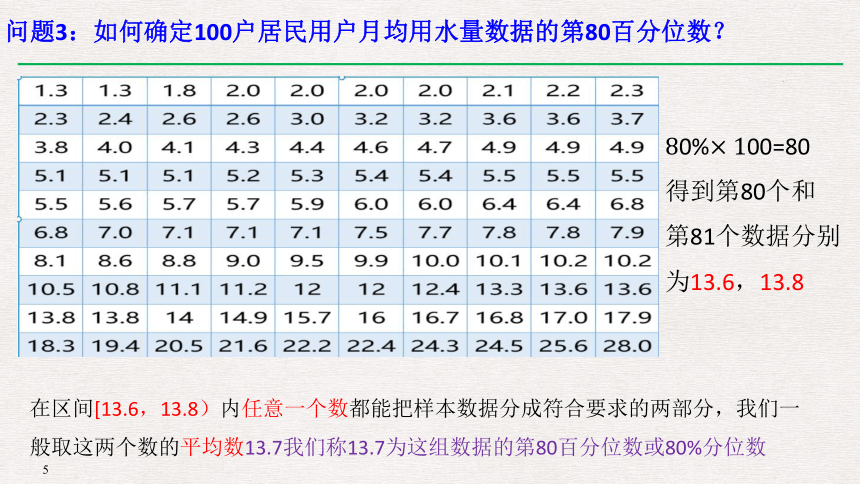
问题3:如何确定100户居民用户月均用水量数据的第80百分位数?
0%00=80
得到第80个和
第81个数据分别为13.6,13.8
在区间[13.6,13.8)内任意一个数都能把样本数据分成符合要求的两部分,我们一般取这两个数的平均数13.7我们称13.7为这组数据的第80百分位数或80%分位数
根据样本数据的第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间会存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作的方便,可以建议市政府把月均用水量标准定为14t,或者把年用水量标准定为168t
你认为14t这个标准一定能够保证80%的居民用水不超标吗?如果不一定,那么哪些环节可能会导致结论的差别
误差主要来自于抽样的方法和样本的随机性
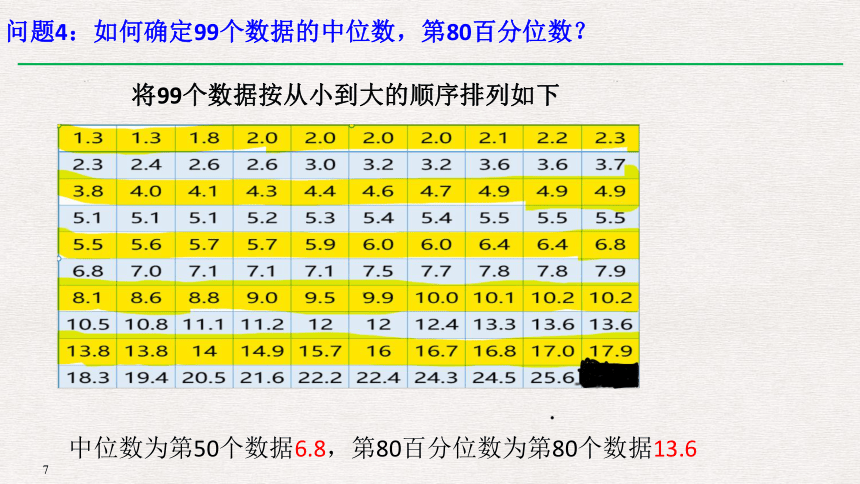
问题4:如何确定99个数据的中位数,第80百分位数?
将99个数据按从小到大的顺序排列如下
中位数为第50个数据6.8,第80百分位数为第80个数据13.6
回忆初中对中位数的定义
中位数,又称中值,指按从小到大顺序排列的一组数据中居于中间位置的数。
(一)计算方法。
将一组数据按照大小的顺序排列。如果数据的个数是奇数,则中间那个数据就是这群数据的中位数;
如果数据的个数是偶数,则中间那 2 个数据的算术平均值就是这群数据的中位数。
问题5:类比中位数的定义,你能给出百分位数的一般定义吗?
你认为下列关于第五十百分位数的说法那个是正确的?对于不正确的说法,你能举出反例吗?
一组数据中的第五十百分位数是这样的一个值:这组数据中
有50%的数据小于它,有50%的数据大于它
有50%的数据小于等于它,有50%的数据数据大于等于它
至少有50%的数据小于等于它,至少有50%的数据数据大于等于它
1.第p百分位数的定义
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中
_________________的数据_______________这个值,
_________________的数据_______________这个值.
新知梳理
P%
(1—P)%
第p百分位数(p%分位数)
至少有
小于或等于
至少有(100-p)%
大于或等于
百分位数是刻画一组样本数据百分位置的量
第p百分位数的定义
新知应用
练习1
1.1,2,3,4,5,6,6,8,910这组数据中的第0百分位数是_____,第50百分位数是______,第100分位数是______.
2.若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
3.若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
4.1,2,3,4,5,6,6,8,910这组数据中的第72百分位数是_____,第79百分位数是______.
P%
(1—P)%
第p百分位数(p%分位数)
第1步,按___________排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的__________.
从小到大
平均数
练习2.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
解析 把该组数据按照由小到大排列,可得:
2.1,3.0,3.2,3.4,3.8,4.0,4.2,4.4,5.3,5.6,
由i=10×25%=2.5,不是整数,则第3个数据3.2,是第25百分位数.
答案 A
2. 问题7:如何计算一组n个数据的第p百分位数的步骤
新知探究
1.第p百分位数有什么特点?
2.某组数据的第p百分位数在此组数据中一定存在吗?为什么
总体数据中的任意一个数小于或等于它的可能性是p.
_____________________这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数,其中________________也称为第一四分位数或下四分位数,_________________也称为第三四分位数或上四分位数.
四分位数
25%,50%,75%
第25百分位数
第75百分位数
50%
25%
75%
另外,第1百 分位数,第5百分位数,第95百分位数和第99百分位数 在统计中也经常被使用
求下列数据的四分位数.
13,15,12,27,22,24,28,30,31,18,19,20,
解 把12个数据按从小到大的顺序排列可得:
12,13,15,18,19,20,22,24,27,28,30,31,
计算12×25%=3,12×50%=6,12×75%=9,
例题分析
根据表格分析:月均用水量样本数据的第80分位数呢?
解:由表可知,月均用水量在13.2t
以下的居民用户所占比例为
23%+32%+13%+9%=77%.
在16.2t以下的居民用户所占的
比例为 77%+9%=86%.
因此,80%分位数一定位于
[13.2,16.2)内.
假设样本在区间上均匀地分布
4.2
1.2
7.2
10.2
16.2
13.2
19.2
22.2
25.2
28.2
23%
55%
77%
86%
68%
91%
94%
98%
100%
解析:
3=1
13.2+1=14.2
同理如何求95%分位数
80%
95%
22.2+3=22.95
课堂练习
某市为了鼓励市民节约用电,实行“阶梯式”电价,为了了解居民的用电情况,通过抽样获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图.若这100户居民中,今年1月份用电费用不超过400千瓦时的占80%,
(1)求a,b的值.
(2)根据求得的a,b值计算用电量的75%分位数和15%分位数.
1.设75%分位数为m,
因为用电量低于300千瓦时的所占比例为(0.001+0.002+0.003)×100=60%,
用电量不超过400千瓦时的占80%,
所以75%分位数为m在[300,400)内,所以0.6+(m-300)×0.002=0.75,
2.设15%分位数为x,
因为用电量低于100千瓦时的所占比例为0.001×100=10%,用电量不超过200千瓦时的占30%,
所以15%分位数为x在[100,200)内,所以0.1+(x-100)×0.002=0.15,解得x=125千瓦时,即用电量的15%分位数为125千瓦时.
课堂总结
1.通过学习和应用百分位数,重点培养数据分析素养、数学运算和数学建模素养.
2.求一组数据的百分位数时,掌握其步骤:
①按照从小到大排列原始数据;
②计算i=n×p%;
③若i不是整数,大于i的最小整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
9.2.2总体百分数的估计
创设情境
通过简单随机抽样,获得某市100户居民用户的月均用水量数据如图所示,请依此估计全市居民的月均用水量
问题引导
问题2 如果市政府希望使的居民用户生活用水费支出不受影响,根据这户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
分析:根据市政府的要求确定居民用户月均用水量标准,就是要寻找一个数,使得全市居民用户月均用水量不超过的占大于的占.
80%
20%
50%
50%
a
a
中位数(第50百分位数,50%分位数)
第80百分位数(80%分位数)
类比抽象,探究新知
问题3:如何确定100户居民用户月均用水量数据的第80百分位数?
0%00=80
得到第80个和
第81个数据分别为13.6,13.8
在区间[13.6,13.8)内任意一个数都能把样本数据分成符合要求的两部分,我们一般取这两个数的平均数13.7我们称13.7为这组数据的第80百分位数或80%分位数
根据样本数据的第80百分位数,我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间会存在偏差,而在决策问题中,只要临界值近似为第80百分位数即可,因此为了实际中操作的方便,可以建议市政府把月均用水量标准定为14t,或者把年用水量标准定为168t
你认为14t这个标准一定能够保证80%的居民用水不超标吗?如果不一定,那么哪些环节可能会导致结论的差别
误差主要来自于抽样的方法和样本的随机性
问题4:如何确定99个数据的中位数,第80百分位数?
将99个数据按从小到大的顺序排列如下
中位数为第50个数据6.8,第80百分位数为第80个数据13.6
回忆初中对中位数的定义
中位数,又称中值,指按从小到大顺序排列的一组数据中居于中间位置的数。
(一)计算方法。
将一组数据按照大小的顺序排列。如果数据的个数是奇数,则中间那个数据就是这群数据的中位数;
如果数据的个数是偶数,则中间那 2 个数据的算术平均值就是这群数据的中位数。
问题5:类比中位数的定义,你能给出百分位数的一般定义吗?
你认为下列关于第五十百分位数的说法那个是正确的?对于不正确的说法,你能举出反例吗?
一组数据中的第五十百分位数是这样的一个值:这组数据中
有50%的数据小于它,有50%的数据大于它
有50%的数据小于等于它,有50%的数据数据大于等于它
至少有50%的数据小于等于它,至少有50%的数据数据大于等于它
1.第p百分位数的定义
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中
_________________的数据_______________这个值,
_________________的数据_______________这个值.
新知梳理
P%
(1—P)%
第p百分位数(p%分位数)
至少有
小于或等于
至少有(100-p)%
大于或等于
百分位数是刻画一组样本数据百分位置的量
第p百分位数的定义
新知应用
练习1
1.1,2,3,4,5,6,6,8,910这组数据中的第0百分位数是_____,第50百分位数是______,第100分位数是______.
2.若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
3.若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
4.1,2,3,4,5,6,6,8,910这组数据中的第72百分位数是_____,第79百分位数是______.
P%
(1—P)%
第p百分位数(p%分位数)
第1步,按___________排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的__________.
从小到大
平均数
练习2.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
解析 把该组数据按照由小到大排列,可得:
2.1,3.0,3.2,3.4,3.8,4.0,4.2,4.4,5.3,5.6,
由i=10×25%=2.5,不是整数,则第3个数据3.2,是第25百分位数.
答案 A
2. 问题7:如何计算一组n个数据的第p百分位数的步骤
新知探究
1.第p百分位数有什么特点?
2.某组数据的第p百分位数在此组数据中一定存在吗?为什么
总体数据中的任意一个数小于或等于它的可能性是p.
_____________________这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数,其中________________也称为第一四分位数或下四分位数,_________________也称为第三四分位数或上四分位数.
四分位数
25%,50%,75%
第25百分位数
第75百分位数
50%
25%
75%
另外,第1百 分位数,第5百分位数,第95百分位数和第99百分位数 在统计中也经常被使用
求下列数据的四分位数.
13,15,12,27,22,24,28,30,31,18,19,20,
解 把12个数据按从小到大的顺序排列可得:
12,13,15,18,19,20,22,24,27,28,30,31,
计算12×25%=3,12×50%=6,12×75%=9,
例题分析
根据表格分析:月均用水量样本数据的第80分位数呢?
解:由表可知,月均用水量在13.2t
以下的居民用户所占比例为
23%+32%+13%+9%=77%.
在16.2t以下的居民用户所占的
比例为 77%+9%=86%.
因此,80%分位数一定位于
[13.2,16.2)内.
假设样本在区间上均匀地分布
4.2
1.2
7.2
10.2
16.2
13.2
19.2
22.2
25.2
28.2
23%
55%
77%
86%
68%
91%
94%
98%
100%
解析:
3=1
13.2+1=14.2
同理如何求95%分位数
80%
95%
22.2+3=22.95
课堂练习
某市为了鼓励市民节约用电,实行“阶梯式”电价,为了了解居民的用电情况,通过抽样获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图.若这100户居民中,今年1月份用电费用不超过400千瓦时的占80%,
(1)求a,b的值.
(2)根据求得的a,b值计算用电量的75%分位数和15%分位数.
1.设75%分位数为m,
因为用电量低于300千瓦时的所占比例为(0.001+0.002+0.003)×100=60%,
用电量不超过400千瓦时的占80%,
所以75%分位数为m在[300,400)内,所以0.6+(m-300)×0.002=0.75,
2.设15%分位数为x,
因为用电量低于100千瓦时的所占比例为0.001×100=10%,用电量不超过200千瓦时的占30%,
所以15%分位数为x在[100,200)内,所以0.1+(x-100)×0.002=0.15,解得x=125千瓦时,即用电量的15%分位数为125千瓦时.
课堂总结
1.通过学习和应用百分位数,重点培养数据分析素养、数学运算和数学建模素养.
2.求一组数据的百分位数时,掌握其步骤:
①按照从小到大排列原始数据;
②计算i=n×p%;
③若i不是整数,大于i的最小整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
