等边三角形[上学期]
图片预览


文档简介
课件15张PPT。自学指导:
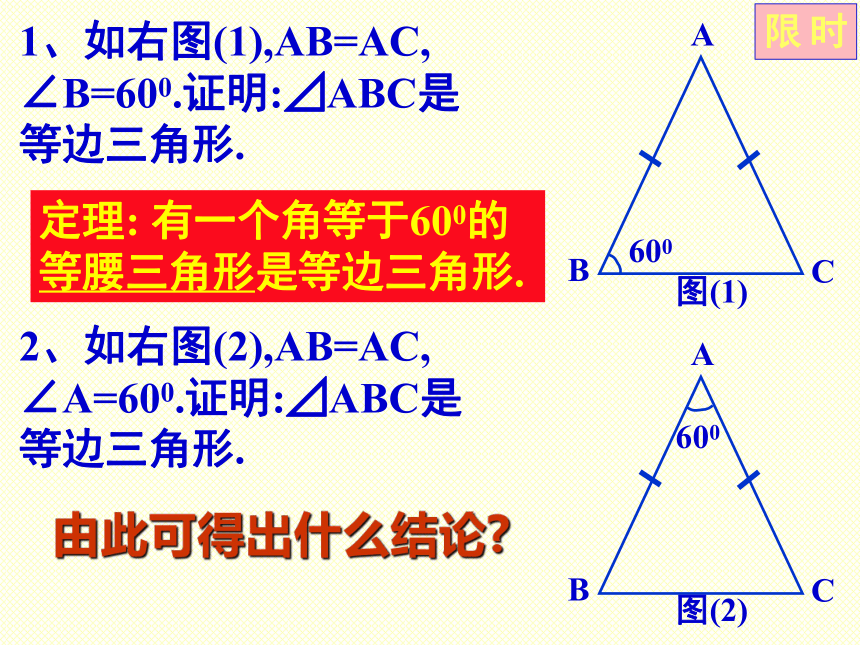
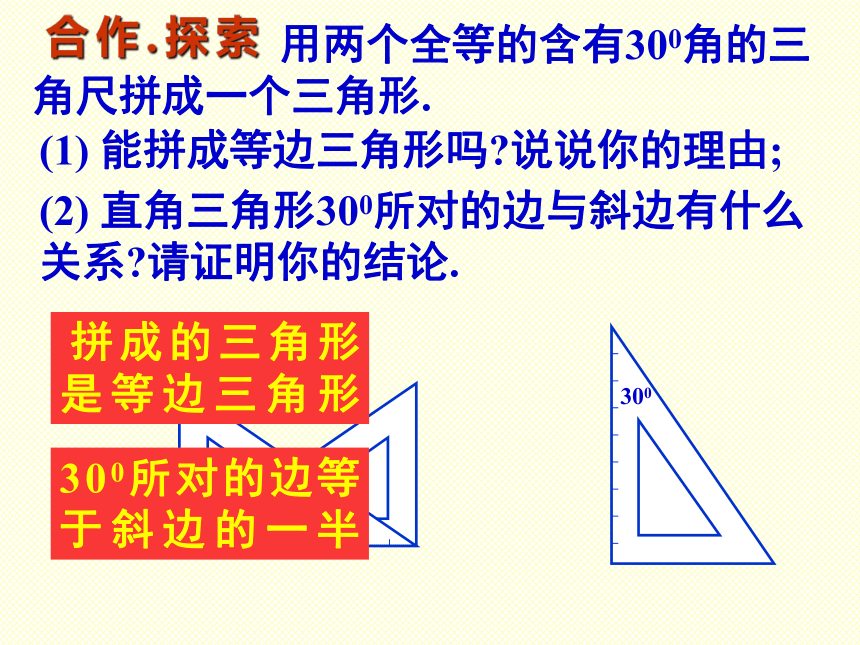
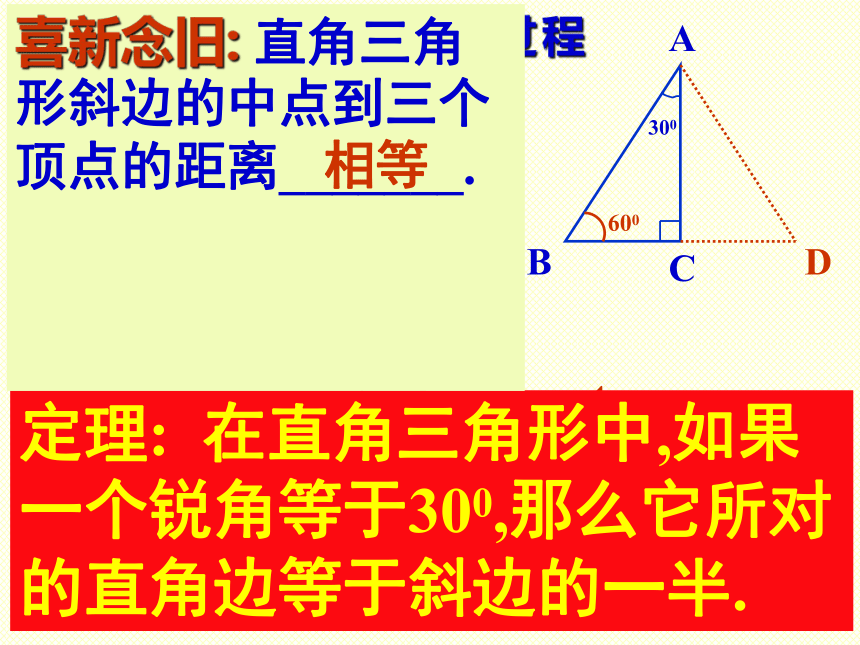
1、怎样才能是一个等腰三角形?2、在一个等腰三角形中,添加什么条件才能是等边三角形,说明理由?3、等边三角形有什么性质?4、等边三角形与直角三角形有何联系?如何证明?1、如右图(1),AB=AC, ∠B=600.证明:⊿ABC是等边三角形.2、如右图(2),AB=AC, ∠A=600.证明:⊿ABC是等边三角形.限时由此可得出什么结论?定理: 有一个角等于600的 等腰三角形是等边三角形.合作.探索 用两个全等的含有300角的三角尺拼成一个三角形.(1) 能拼成等边三角形吗?说说你的理由;(2) 直角三角形300所对的边与斜边有什么关系?请证明你的结论. 拼成的三角形是等边三角形300所对的边等于斜边的一半推理证明过程证明: 如右图,在⊿ABC中,∵∠ACB=900,∠A=300,∴ ∠B=600. 延长BC至D, 使得CD=CB,连结AC.DBC=DC ∠BCA=∠BCAAC=AC⊿ABC≌⊿ADC(ASA),AB=AD ⊿ABD是等边三角形定理: 在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半.喜新念旧: 直角三角形斜边的中点到三个顶点的距离_______.
相等基础练习1)在Rt⊿ABC, ∠C=900, ∠A=300 ,AB=4,则BC=_____,AC=______
2)在Rt⊿ABC, ∠C=900, ∠A=600 ,AB=4,则BC=_____,AC=______
3)在Rt⊿ABC, ∠C=900, ∠A=300 ,AB=4,则⊿ABC的面积=______
4)在Rt⊿ABC, ∠C=900, ∠A=300 ,CB=4,则AB=_____,AC=______
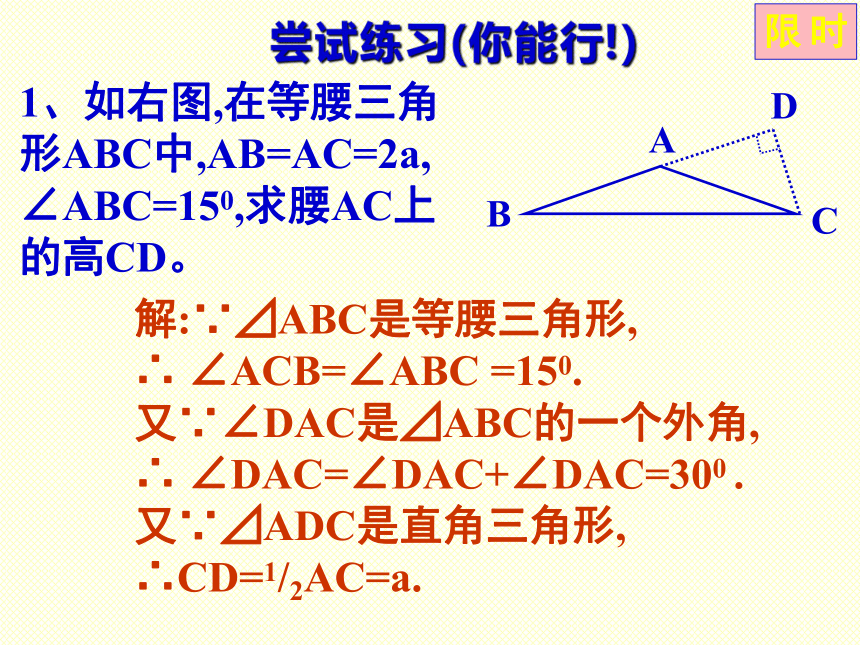
尝试练习(你能行!)限时解:∵⊿ABC是等腰三角形, ∴ ∠ACB=∠ABC =150. 又∵∠DAC是⊿ABC的一个外角, ∴ ∠DAC=∠DAC+∠DAC=300 . 又∵⊿ADC是直角三角形, ∴CD=1/2AC=a.尝试练习(你能行!)限时2、如右图,在四边 形ABCD中,AB=2, CD=1 ∠A=600,求四边形ABCD的面积。E30°课堂作业限时证明: ∵ ⊿ABC是等边三角形,且DE//BC, ∴∠ADE=∠B=600,∠AED= ∠C=600, ∴ ∠A=600, ∴ ⊿ADE是等边三角形.限时ABCDE2.房梁的一部分如图所示,其中BC⊥AC,∠A=300,AB=7.4m,点D是AB的中点,且DE ⊥ AC,垂足为E,求BC,DE的长.解:∵⊿ACB是Rt⊿, ∠ACB=900, ∠A=300, ∴∠B=600, BC=1/2AB=3.7m. 又∵ DE ⊥ AC , BC⊥AC, ∴DE//BC, ∴⊿AED∽⊿ACB. 又D是AB的中点, ∴DE=1/2BC=1.85m.证明:∵⊿ABC是等边三角形,BC//EF, AC//DE, ∴∠EAB=∠ABC=600,∠EAB=∠BAC=600, ∴∠E=600, ∴⊿AEB是等边三角形. 同理可证:∠D=600,∠F=600. ∴ ⊿ABC, ⊿DEF, ⊿ABE, ⊿BCD, ⊿ACF都是等边三角形.限时“试一试”,你就知!1、命题“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于300”是真命题吗?为什么?解:如右图, 设⊿ACB是Rt⊿,且BC=1/2AB. 取AB的中点C,连结CD, 则 DA=DC=DB, ∴CB=BD=DC, ∴∠CBA=600 , ∴∠CBA=300 .注:以后上面的结论可以当作定理来运用.限时2、如下图(1),ABCD是一张正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上(如图(2)),折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?(提示:利用第1题的结论)限时111300600150课堂总结1、定理: 有一个角等于600的等腰三角形是等边三角形.2、定理: 在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半.3、定理: 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于300
1、怎样才能是一个等腰三角形?2、在一个等腰三角形中,添加什么条件才能是等边三角形,说明理由?3、等边三角形有什么性质?4、等边三角形与直角三角形有何联系?如何证明?1、如右图(1),AB=AC, ∠B=600.证明:⊿ABC是等边三角形.2、如右图(2),AB=AC, ∠A=600.证明:⊿ABC是等边三角形.限时由此可得出什么结论?定理: 有一个角等于600的 等腰三角形是等边三角形.合作.探索 用两个全等的含有300角的三角尺拼成一个三角形.(1) 能拼成等边三角形吗?说说你的理由;(2) 直角三角形300所对的边与斜边有什么关系?请证明你的结论. 拼成的三角形是等边三角形300所对的边等于斜边的一半推理证明过程证明: 如右图,在⊿ABC中,∵∠ACB=900,∠A=300,∴ ∠B=600. 延长BC至D, 使得CD=CB,连结AC.DBC=DC ∠BCA=∠BCAAC=AC⊿ABC≌⊿ADC(ASA),AB=AD ⊿ABD是等边三角形定理: 在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半.喜新念旧: 直角三角形斜边的中点到三个顶点的距离_______.
相等基础练习1)在Rt⊿ABC, ∠C=900, ∠A=300 ,AB=4,则BC=_____,AC=______
2)在Rt⊿ABC, ∠C=900, ∠A=600 ,AB=4,则BC=_____,AC=______
3)在Rt⊿ABC, ∠C=900, ∠A=300 ,AB=4,则⊿ABC的面积=______
4)在Rt⊿ABC, ∠C=900, ∠A=300 ,CB=4,则AB=_____,AC=______
尝试练习(你能行!)限时解:∵⊿ABC是等腰三角形, ∴ ∠ACB=∠ABC =150. 又∵∠DAC是⊿ABC的一个外角, ∴ ∠DAC=∠DAC+∠DAC=300 . 又∵⊿ADC是直角三角形, ∴CD=1/2AC=a.尝试练习(你能行!)限时2、如右图,在四边 形ABCD中,AB=2, CD=1 ∠A=600,求四边形ABCD的面积。E30°课堂作业限时证明: ∵ ⊿ABC是等边三角形,且DE//BC, ∴∠ADE=∠B=600,∠AED= ∠C=600, ∴ ∠A=600, ∴ ⊿ADE是等边三角形.限时ABCDE2.房梁的一部分如图所示,其中BC⊥AC,∠A=300,AB=7.4m,点D是AB的中点,且DE ⊥ AC,垂足为E,求BC,DE的长.解:∵⊿ACB是Rt⊿, ∠ACB=900, ∠A=300, ∴∠B=600, BC=1/2AB=3.7m. 又∵ DE ⊥ AC , BC⊥AC, ∴DE//BC, ∴⊿AED∽⊿ACB. 又D是AB的中点, ∴DE=1/2BC=1.85m.证明:∵⊿ABC是等边三角形,BC//EF, AC//DE, ∴∠EAB=∠ABC=600,∠EAB=∠BAC=600, ∴∠E=600, ∴⊿AEB是等边三角形. 同理可证:∠D=600,∠F=600. ∴ ⊿ABC, ⊿DEF, ⊿ABE, ⊿BCD, ⊿ACF都是等边三角形.限时“试一试”,你就知!1、命题“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于300”是真命题吗?为什么?解:如右图, 设⊿ACB是Rt⊿,且BC=1/2AB. 取AB的中点C,连结CD, 则 DA=DC=DB, ∴CB=BD=DC, ∴∠CBA=600 , ∴∠CBA=300 .注:以后上面的结论可以当作定理来运用.限时2、如下图(1),ABCD是一张正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上(如图(2)),折痕交AE于点G,那么∠ADG等于多少度?你能证明你的结论吗?(提示:利用第1题的结论)限时111300600150课堂总结1、定理: 有一个角等于600的等腰三角形是等边三角形.2、定理: 在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半.3、定理: 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于300
