等腰三角形[上学期]

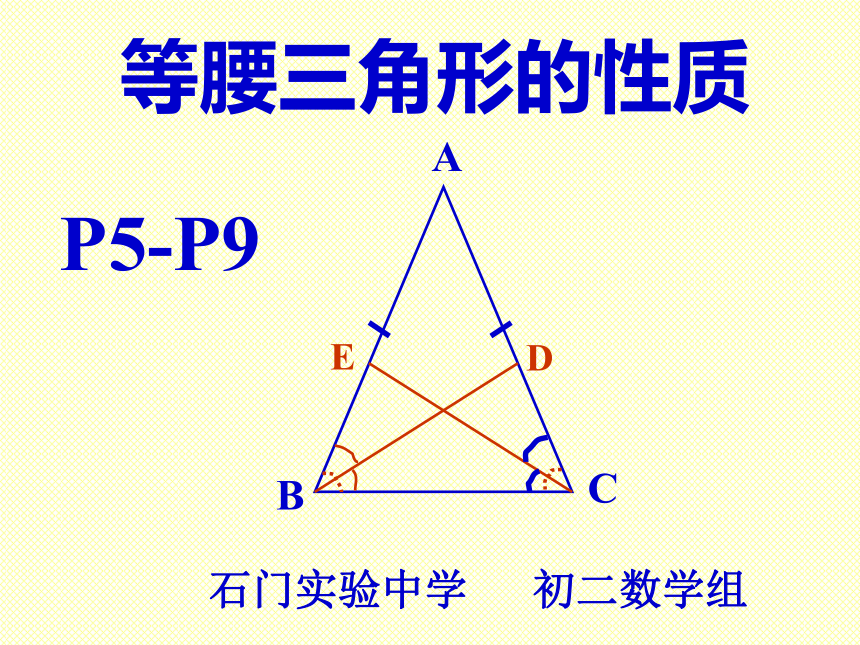
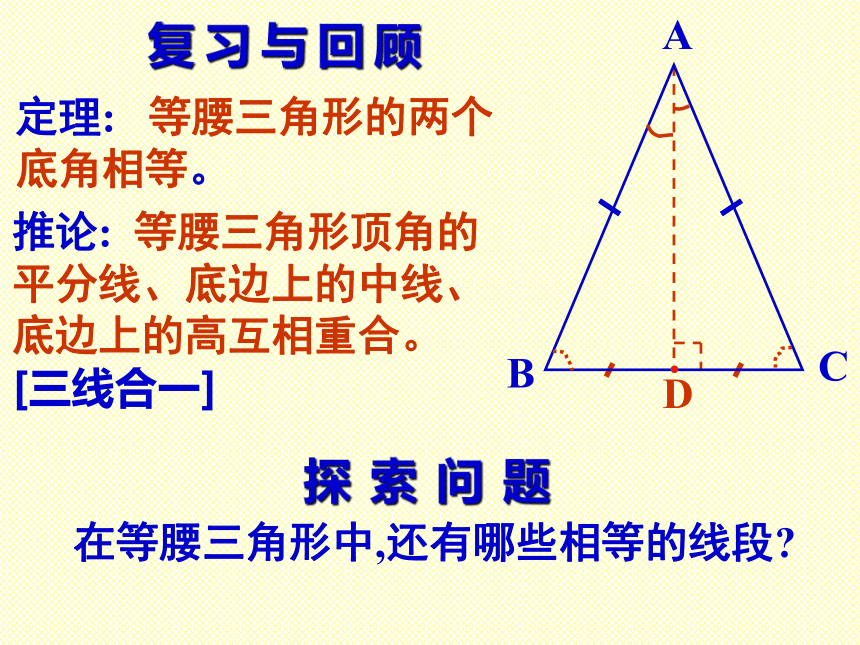
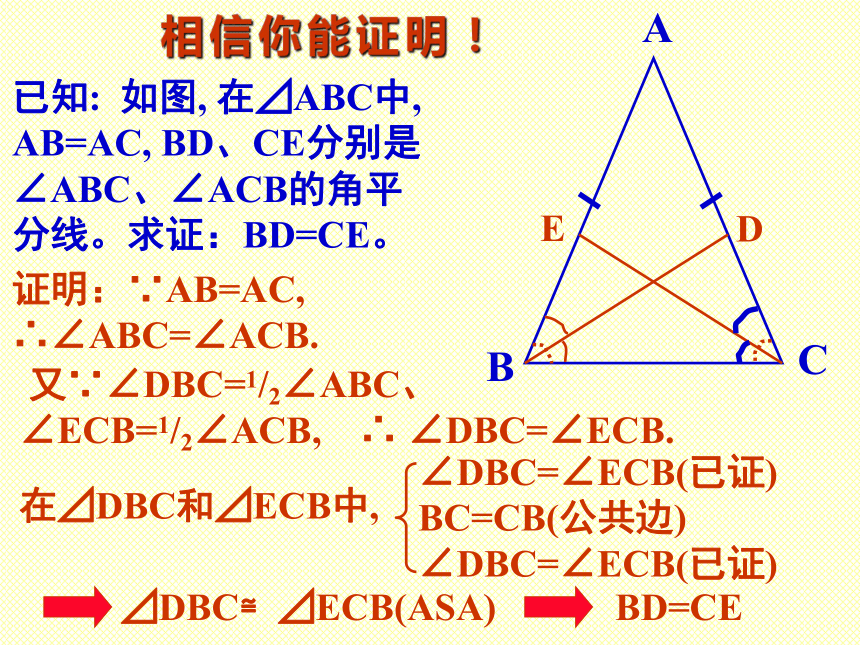
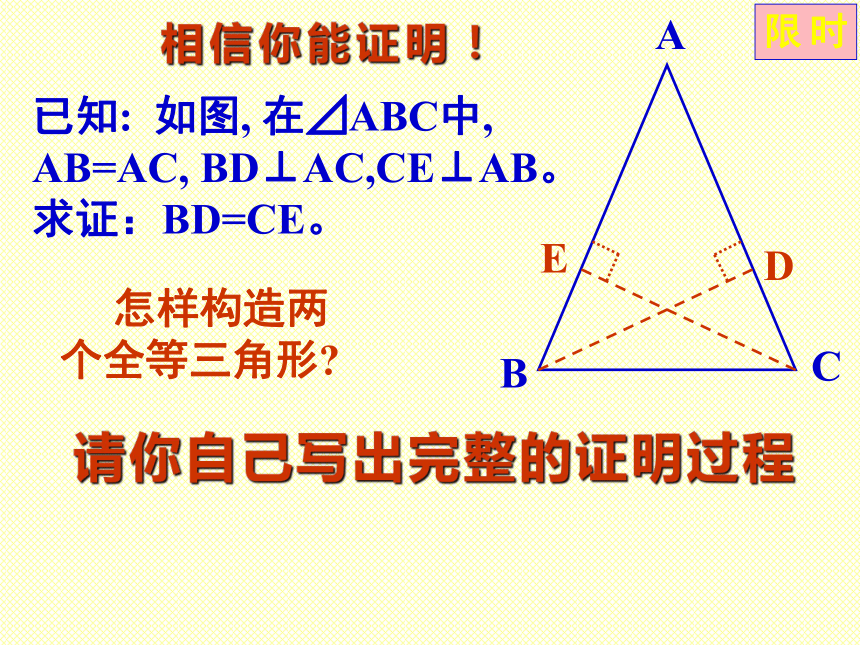
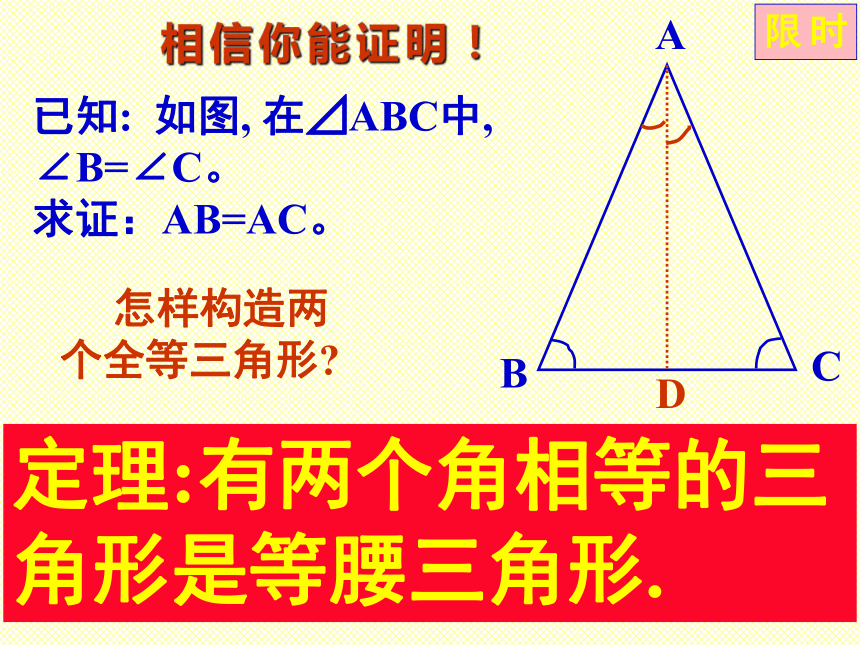
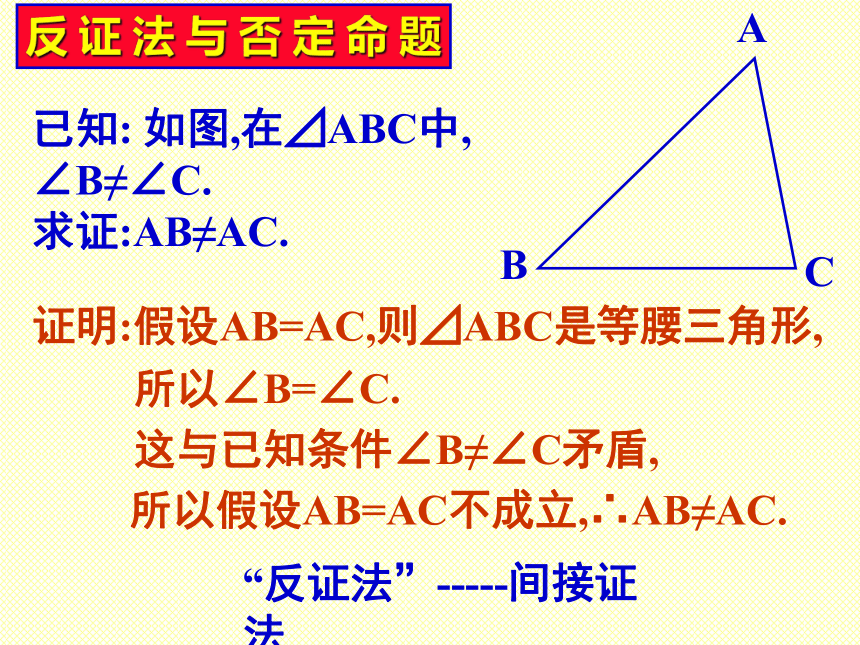
课件15张PPT。等腰三角形的性质石门实验中学 初二数学组 P5-P9D定理: 等腰三角形的两个底角相等。推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。 [三线合一]复习与回顾探索问题在等腰三角形中,还有哪些相等的线段?DE已知: 如图, 在⊿ABC中, AB=AC, BD、CE分别是∠ABC、∠ACB的角平 分线。求证：BD=CE。相信你能证明！证明：∵AB=AC, ∴∠ABC=∠ACB.在⊿DBC和⊿ECB中, 又∵∠DBC=1/2∠ABC、 ∠ECB=1/2∠ACB, ∴ ∠DBC=∠ECB.⊿DBC≌⊿ECB(ASA)BD=CEABC已知: 如图, 在⊿ABC中, AB=AC, D、E分别是AB、AC的中点。 求证：BD=CE。相信你能证明！限时请你自己写出完整的证明过程 怎样构造两个全等三角形?ABC已知: 如图, 在⊿ABC中, AB=AC, BD⊥AC,CE⊥AB。 求证：BD=CE。相信你能证明！限时请你自己写出完整的证明过程 怎样构造两个全等三角形?ABC已知: 如图, 在⊿ABC中, ∠B=∠C。 求证：AB=AC。相信你能证明！限时请你自己写出完整的证明过程 怎样构造两个全等三角形?定理:有两个角相等的三角形是等腰三角形.已知: 如图,在⊿ABC中, ∠B≠∠C. 求证:AB≠AC.反证法与否定命题证明:假设AB=AC,则⊿ABC是等腰三角形,所以假设AB=AC不成立,∴AB≠AC.所以∠B=∠C.这与已知条件∠B≠∠C矛盾,“反证法”-----间接证法“反证法”威力无比!课堂作业[习题1.2]1. 已知: 如图,∠CAE是⊿ABC的外角,AD//BC, 且 ∠1=∠2. 求证:AB=AC.请你自己写出完整的证明过程2.如图,在一个风筝ABCD中,AB=AD,BC=DC,分别在AB,AD的中点E,F处拉两根彩线EC,FC. 证明: 这两根彩线的长相等.请你自己写出完整的证明过程3.如图,一艘船从A处出发,以18节的速度向正北航行,经过10时到达B处.分别从A,B望灯塔C,测得∠NAC=420,∠NBC=840.求从B处到灯塔C的距离.请你自己写出完整的求解过程证明:在一个三角形中,至少有一个内角小于或等于600. 用什么方法证明? 请你 自己写出完整的证明过程成功者的摇篮1.用反证法证明：一个三角形中不能有两个角是直角
已知：△ABC．
求证：∠A、∠B、∠C中不能有两个角是直角．证明：假设∠A、∠B、∠C中有两个角是直角，不妨设∠A=∠B=90°，则
∠A+∠B+∠C=90°+90°+∠C＞180°．
这与三角形内角和定理矛盾，
所以∠A=∠B=90°不成立．
所以一个三角形中不能有两个角是直角．课堂总结定理: 等腰三角形的两个底角相等。推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。[三线合一]定理:有两个角相等的三角形是等腰三角形。推论: 等腰三角形底角平分线、两腰上的中线、两腰上的高相等。反证法：证明的思想、方法。26.“三等分角”是数学史上一个著　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　名的问题,但仅用尺规不可能 “三　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　等分角”,下面是数学家帕普斯借　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　助函数给出的一种“三等分锐角”的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　方法(如图)将给定的锐角∠AOB置 于直角坐标系x轴上、边OA与函数 y=1/x的图象交于点P,以P为圆心、 以2OP为半径作弧交图象于点R.分 别过点P和R作x轴和y轴的平行线， 两直线相交于点M ,连接OM得到∠MOB,则∠MOB=1/3∠AOB,要明白帕普斯的方法,请研究以下问题:
(1) 设P(a,1/a)、R(b,1/b) ,求直线OM对应的函数表达式(用含a,b的代数式表示). (3分)
(2) 分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=1/3∠AOB． (7分)
(3) 应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明). (1分)、佛山中考题中考全接触(A班)