广东省中山市名校2022-2023学年高一下学期期中考试数学试题(含答案)
文档属性
| 名称 | 广东省中山市名校2022-2023学年高一下学期期中考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 17:30:18 | ||
图片预览




文档简介
中山市名校2022-2023学年高一下学期期中考试
数学
一、选择题(本题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出最符合题目要求的一项)
1.为了营造浓厚的校园体育氛围,学校采用按比例分层抽样的方法从高一550人,高二500人,高三450人中抽取60人观看排球决赛,那么高一年级被抽取的人数为( )。
A.18 B.20 C.22 D.30
2.在空间中,下列说法正确的是( )。
A.垂直于同一直线的两条直线平行 B.垂直于同一直线的两条直线垂直
C.平行于同一平面的两条直线平行 D.垂直于同一平面的两条直线平行
3.如图所示,是水平放置的的斜二测直观图,其中,则以下说法正确的是( )。
A.是钝角三角形 B.的面积是的面积的2倍
C.点的坐标为 D.的周长是
4.17世纪30年代,意大利数学家卡瓦列利在《不可分量几何学》一书中介绍了利用平面图形旋转计算球体体积的方法.如图,是一个半圆,圆心为,是半圆的外切矩形.以直线为轴将该平面图形旋转一周,记,阴影部分,半圆所形成的几何体的体积分别为,,,则下列说法正确的是( )。
A. B. C. D.
5.已知中,点是线段的中点,,则( )。
A. B. C. D.
6.要得到的图象,只需将函数的图象( )。
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
7.已知函数,若,是锐角三角形的两个内角,则一定有( )。
A. B.
C. D.
8.已知点为的重心,设的内角,,的对边为,,且满足向量,若,则实数( )。
A. B. C.2 D.3
二、多选题(本题共4小题,每小题5分,共20分.在每小题列出的四个选项中,有至少两个正确选项,全部选对得5分,部分选对得2分,有错选得0分)。
9.下列命题正确的是( )。
A.若向量,满足,则,为平行向量。
B.已知平面内的一组基底,,则向量,也能作为一组基底。
C.模等于1个单位长度的向量是单位向量,所有单位向量均相等。
D.若是等边三角形,则。
10.已知.对任意的均有,则( )。
A. B.
C. D.
11.在锐角中,内角,,的对边分别为,,,,且,则下列结论正确的是( )。
A. B. C. D.
12.如图,四棱锥的底面为菱形,,,底面,是上任意一点(不含端点),则下列结论中正确的是( )。
A.若平面,则。
B.到平面的距离为。
C.当为中点时,过、、的截面为直角梯形。
D.当为中点时,有最小值。
三、填空题(本题共4小题,每小题5分,共20分.在横线处填写最符合题意要求的答案)
13.一家水果店的老板为了解本店苹果的日销售情况,记录了过去10天苹果的日销售量(单位:kg):83,96,107,91,74,75,94,80,80,100;则该水果店过去10天苹果日销售量的中位数为______.
14.LED(发光二极管)是一种能够将电能转化为可见光的固态的半导体器件,它可以直接把电转化为光.LED灯的抗震性能非常好,被广泛运用于手机、台灯、家电等日常家电.如图,小明同学发现家里的LED灯是正六边形形状的,其平面图可简化为正六边形,若向量在向量方向上的投影向量为,则实数______.
15.在中,内角,,所对的边分别为,,,已知的面积为3,,,则的值为______.
16.在梯形中,,,,将沿折起,连接,得到三棱锥,三棱锥体积的最大值为______;此时该三棱锥的外接球的表面积为______.
四、解答题(本题共6小题,共70分.解答题应写出文字说明、证明过程和验算步骤)
17.已知,,,
(1)求的值;
(2)求的值。
18.为庆祝“五四”青年节,广州市有关单位举行了“五四”青年节团知识竞赛活动,为了解全市参赛者成绩的情况,从所有参赛者中随机抽样抽取100名,将其成绩整理后分为6组,画出频率分布直方图如图所示(最低90分,最高150分),但是第一、二两组数据丢失,只知道第二组的频率是第一组的2倍。
(1)求第一组、第二组的频率各是多少?并补齐频率分布直方图;
(2)现划定成绩大于或等于上四分位数即第75百分位数为“良好”以上等级,根据直方图,估计全市“良好”以上等级的成绩范围(保留1位小数);
(3)现知道直方图中成绩在内的平均数为136,在内的平均数为144,求成绩在内的平均数。
19.已知,,与的夹角为,函数;
(1)求函数最小正周期和对称中心;
(2)若锐角中,角,,的对边分别为,,,且,求的取值范围。
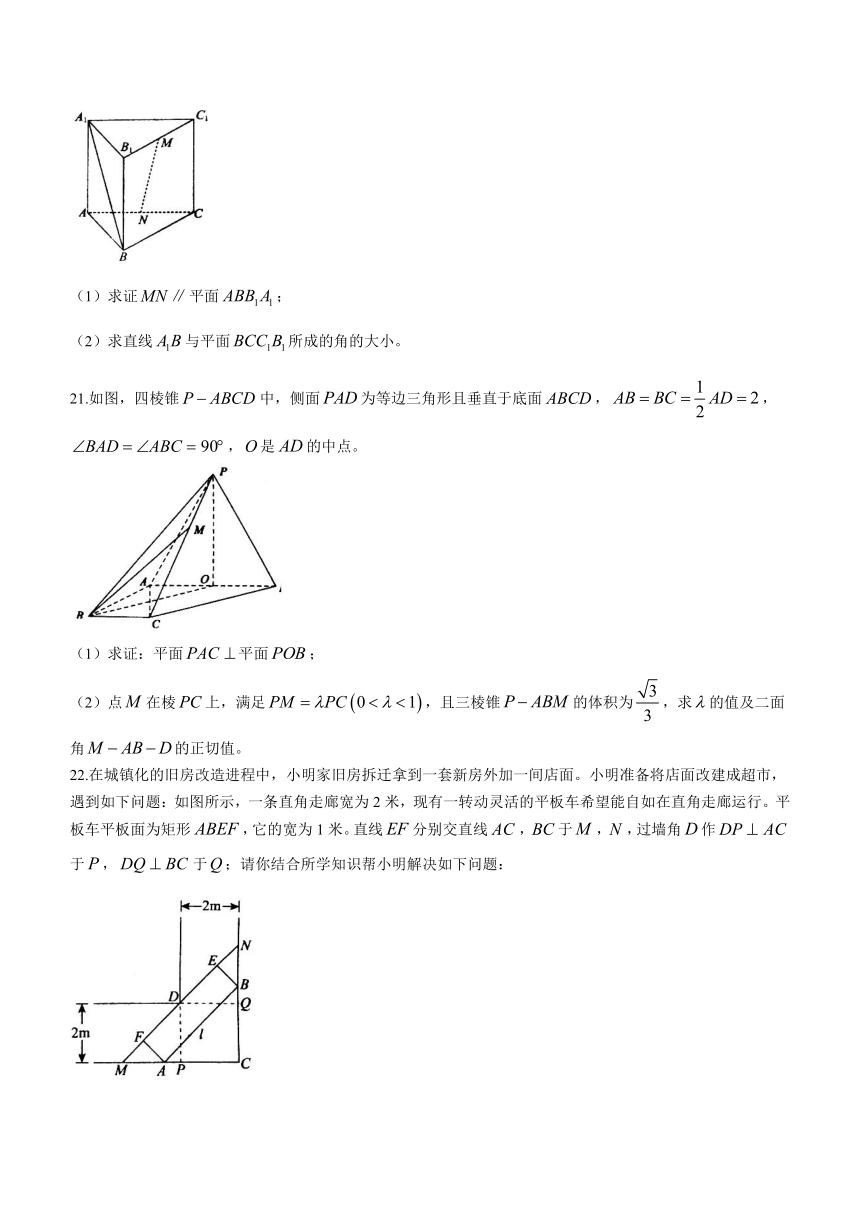
20.如图,在直三棱柱中,,,是的中点,是的中点。
(1)求证平面;
(2)求直线与平面所成的角的大小。
21.如图,四棱锥中,侧面为等边三角形且垂直于底面,,,是的中点。
(1)求证:平面平面;
(2)点在棱上,满足,且三棱锥的体积为,求的值及二面角的正切值。
22.在城镇化的旧房改造进程中,小明家旧房拆迁拿到一套新房外加一间店面。小明准备将店面改建成超市,遇到如下问题:如图所示,一条直角走廊宽为2米,现有一转动灵活的平板车希望能自如在直角走廊运行。平板车平板面为矩形,它的宽为1米。直线分别交直线,于,,过墙角作于,于;请你结合所学知识帮小明解决如下问题:
(1)若平板车卡在直角走廊内,且,,试将平板面的长表示为的函数;
(2)若平板车要想顺利通过直角走席,其长度不能超过多少米?
中山市名校2022-2023学年高一下学期期中考试
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D D B A D C A ABD BD ACD ABC
13.87 14. 15. 16.
8.【详解】如图,连接延长交交于,由于为重心,故为中点,∵,∴,由重心的性质得,,即,由余弦定理得,,,
∵,,∴,
∴,∴,由,将正切化为正弦与余弦的商,利用正弦定理可得,∴,故选:A.
11.【答案】ACD【详解】由正弦边角关系知:,则,
所以,而,则,A正确;
由上知:,即,B错误,C正确;由知:,则,又,故,则,即,D正确.故选:ACD
12.ABC【详解】∵平面,平面,平面平面∴,A正确;设到平面的距离为,则有,∵,即,则,B正确;当为中点时,如图.
取的中点,连接,,,则,∵,则
∴过、、的截面为,则,,∴,则,即为直角梯形,C正确;借助于侧面展开图,如图,连接交于点,此时为最小值若为中点时,∵,则∴,这与题意相矛盾,D错误;故选:ABC.
15.【答案】【详解】∵,,∴,
∴,∴,又,∴,,
∴∴.故答案为:.
16.【答案】
【详解】过点作,垂足为,∵为等腰梯形,,∴,
∴,由余弦定理得,即∵∴,易知,当平面平面时,三棱锥体积最大,此时,平面,易知,
∴∴,记为外接球球心,半径为
∵平面,∴到平面的距离,又的外接圆半径∴∴
四、解答题
17.【详解】(1),∵,,∴,∴.
(2)由,,求得,,
∴.
18.解:(1)设第一组的频率为,则第二组的频率为,依题意,解得,所以第一组的频率为0.04,则第二组的频率为0.08,补全频率分布直方图如下:
(2)由,设上四分位数为,则,
所以,解得,
所以全市“良好”以上等级的成绩范围;
(3)成绩在内的平均数为;
19.【详解】(1)解:由条件可知:
,,
∴,
∴的最小正周期为,令,,解得,,∴的对称中心为;
(2)解:由正弦定理得,由(1),而,得,∴,,解得,,又,可得,∵,∴,
代入上式化简得:,
又在锐角中,有,∴,∴,则有,∴
20.【详解】(1)如图,取中点,连接,,因为是的中点,所以,,又因为在直三棱柱中,是的中点,所以,,所以,,所以四边形是平行四边形,所以,因为平面,平面,所以平面;
(2)如图,连接,,由直三棱柱的性质可知平面,因为平面,所以,因为,,是的中点,所以,因为,,平面,所以平面,所以是直线与平面所成的角的平面角,因为,,所以不妨设,则,,,所以,则,所以,因为,所以,所以直线与平面所成的角的大小.
21.【详解】(1)连接,因为底面中,,,所以四边形为正方形,所以,因为侧面为等边三角形,是的中点,所以,因为平面平面,平面平面,所以平面,因为平面,所以,因为,所以平面,因为平面,所以平面平面;
(2)因为底面中,,,侧面为等边三角形,是的中点,所以,,,,因为平面,,平面,所以,,所以,
因为,所以,所以,
设点,到平面的距离分别为,,因为,所以,
,解得,因为三棱锥的体积为,
所以,所以,解得,所以,所以,因为,所以,取靠近点的四等份点,连接,则,因为平面,所以平面,因为平面,所以,过点作于,连接,因为,所以平面,因为平面,所以,所以为二面角的平面角,因为,所以,
因为,所以四边形为矩形,所以,
所以在中,,所以二面角的正切值为
22.【详解】(1),,,
,
,所以,
(2)“平板车要想顺利通过直角走廊”即对任意角,平板车的长度,
记,则,又则,
所以,所以,即,则,
记,,则,函数
因为,在上都递增,所以在上都递增,
所以在上的单调递减;当时取得最小值.所以长度不能超过米
数学
一、选择题(本题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出最符合题目要求的一项)
1.为了营造浓厚的校园体育氛围,学校采用按比例分层抽样的方法从高一550人,高二500人,高三450人中抽取60人观看排球决赛,那么高一年级被抽取的人数为( )。
A.18 B.20 C.22 D.30
2.在空间中,下列说法正确的是( )。
A.垂直于同一直线的两条直线平行 B.垂直于同一直线的两条直线垂直
C.平行于同一平面的两条直线平行 D.垂直于同一平面的两条直线平行
3.如图所示,是水平放置的的斜二测直观图,其中,则以下说法正确的是( )。
A.是钝角三角形 B.的面积是的面积的2倍
C.点的坐标为 D.的周长是
4.17世纪30年代,意大利数学家卡瓦列利在《不可分量几何学》一书中介绍了利用平面图形旋转计算球体体积的方法.如图,是一个半圆,圆心为,是半圆的外切矩形.以直线为轴将该平面图形旋转一周,记,阴影部分,半圆所形成的几何体的体积分别为,,,则下列说法正确的是( )。
A. B. C. D.
5.已知中,点是线段的中点,,则( )。
A. B. C. D.
6.要得到的图象,只需将函数的图象( )。
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
7.已知函数,若,是锐角三角形的两个内角,则一定有( )。
A. B.
C. D.
8.已知点为的重心,设的内角,,的对边为,,且满足向量,若,则实数( )。
A. B. C.2 D.3
二、多选题(本题共4小题,每小题5分,共20分.在每小题列出的四个选项中,有至少两个正确选项,全部选对得5分,部分选对得2分,有错选得0分)。
9.下列命题正确的是( )。
A.若向量,满足,则,为平行向量。
B.已知平面内的一组基底,,则向量,也能作为一组基底。
C.模等于1个单位长度的向量是单位向量,所有单位向量均相等。
D.若是等边三角形,则。
10.已知.对任意的均有,则( )。
A. B.
C. D.
11.在锐角中,内角,,的对边分别为,,,,且,则下列结论正确的是( )。
A. B. C. D.
12.如图,四棱锥的底面为菱形,,,底面,是上任意一点(不含端点),则下列结论中正确的是( )。
A.若平面,则。
B.到平面的距离为。
C.当为中点时,过、、的截面为直角梯形。
D.当为中点时,有最小值。
三、填空题(本题共4小题,每小题5分,共20分.在横线处填写最符合题意要求的答案)
13.一家水果店的老板为了解本店苹果的日销售情况,记录了过去10天苹果的日销售量(单位:kg):83,96,107,91,74,75,94,80,80,100;则该水果店过去10天苹果日销售量的中位数为______.
14.LED(发光二极管)是一种能够将电能转化为可见光的固态的半导体器件,它可以直接把电转化为光.LED灯的抗震性能非常好,被广泛运用于手机、台灯、家电等日常家电.如图,小明同学发现家里的LED灯是正六边形形状的,其平面图可简化为正六边形,若向量在向量方向上的投影向量为,则实数______.
15.在中,内角,,所对的边分别为,,,已知的面积为3,,,则的值为______.
16.在梯形中,,,,将沿折起,连接,得到三棱锥,三棱锥体积的最大值为______;此时该三棱锥的外接球的表面积为______.
四、解答题(本题共6小题,共70分.解答题应写出文字说明、证明过程和验算步骤)
17.已知,,,
(1)求的值;
(2)求的值。
18.为庆祝“五四”青年节,广州市有关单位举行了“五四”青年节团知识竞赛活动,为了解全市参赛者成绩的情况,从所有参赛者中随机抽样抽取100名,将其成绩整理后分为6组,画出频率分布直方图如图所示(最低90分,最高150分),但是第一、二两组数据丢失,只知道第二组的频率是第一组的2倍。
(1)求第一组、第二组的频率各是多少?并补齐频率分布直方图;
(2)现划定成绩大于或等于上四分位数即第75百分位数为“良好”以上等级,根据直方图,估计全市“良好”以上等级的成绩范围(保留1位小数);
(3)现知道直方图中成绩在内的平均数为136,在内的平均数为144,求成绩在内的平均数。
19.已知,,与的夹角为,函数;
(1)求函数最小正周期和对称中心;
(2)若锐角中,角,,的对边分别为,,,且,求的取值范围。
20.如图,在直三棱柱中,,,是的中点,是的中点。
(1)求证平面;
(2)求直线与平面所成的角的大小。
21.如图,四棱锥中,侧面为等边三角形且垂直于底面,,,是的中点。
(1)求证:平面平面;
(2)点在棱上,满足,且三棱锥的体积为,求的值及二面角的正切值。
22.在城镇化的旧房改造进程中,小明家旧房拆迁拿到一套新房外加一间店面。小明准备将店面改建成超市,遇到如下问题:如图所示,一条直角走廊宽为2米,现有一转动灵活的平板车希望能自如在直角走廊运行。平板车平板面为矩形,它的宽为1米。直线分别交直线,于,,过墙角作于,于;请你结合所学知识帮小明解决如下问题:
(1)若平板车卡在直角走廊内,且,,试将平板面的长表示为的函数;
(2)若平板车要想顺利通过直角走席,其长度不能超过多少米?
中山市名校2022-2023学年高一下学期期中考试
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D D B A D C A ABD BD ACD ABC
13.87 14. 15. 16.
8.【详解】如图,连接延长交交于,由于为重心,故为中点,∵,∴,由重心的性质得,,即,由余弦定理得,,,
∵,,∴,
∴,∴,由,将正切化为正弦与余弦的商,利用正弦定理可得,∴,故选:A.
11.【答案】ACD【详解】由正弦边角关系知:,则,
所以,而,则,A正确;
由上知:,即,B错误,C正确;由知:,则,又,故,则,即,D正确.故选:ACD
12.ABC【详解】∵平面,平面,平面平面∴,A正确;设到平面的距离为,则有,∵,即,则,B正确;当为中点时,如图.
取的中点,连接,,,则,∵,则
∴过、、的截面为,则,,∴,则,即为直角梯形,C正确;借助于侧面展开图,如图,连接交于点,此时为最小值若为中点时,∵,则∴,这与题意相矛盾,D错误;故选:ABC.
15.【答案】【详解】∵,,∴,
∴,∴,又,∴,,
∴∴.故答案为:.
16.【答案】
【详解】过点作,垂足为,∵为等腰梯形,,∴,
∴,由余弦定理得,即∵∴,易知,当平面平面时,三棱锥体积最大,此时,平面,易知,
∴∴,记为外接球球心,半径为
∵平面,∴到平面的距离,又的外接圆半径∴∴
四、解答题
17.【详解】(1),∵,,∴,∴.
(2)由,,求得,,
∴.
18.解:(1)设第一组的频率为,则第二组的频率为,依题意,解得,所以第一组的频率为0.04,则第二组的频率为0.08,补全频率分布直方图如下:
(2)由,设上四分位数为,则,
所以,解得,
所以全市“良好”以上等级的成绩范围;
(3)成绩在内的平均数为;
19.【详解】(1)解:由条件可知:
,,
∴,
∴的最小正周期为,令,,解得,,∴的对称中心为;
(2)解:由正弦定理得,由(1),而,得,∴,,解得,,又,可得,∵,∴,
代入上式化简得:,
又在锐角中,有,∴,∴,则有,∴
20.【详解】(1)如图,取中点,连接,,因为是的中点,所以,,又因为在直三棱柱中,是的中点,所以,,所以,,所以四边形是平行四边形,所以,因为平面,平面,所以平面;
(2)如图,连接,,由直三棱柱的性质可知平面,因为平面,所以,因为,,是的中点,所以,因为,,平面,所以平面,所以是直线与平面所成的角的平面角,因为,,所以不妨设,则,,,所以,则,所以,因为,所以,所以直线与平面所成的角的大小.
21.【详解】(1)连接,因为底面中,,,所以四边形为正方形,所以,因为侧面为等边三角形,是的中点,所以,因为平面平面,平面平面,所以平面,因为平面,所以,因为,所以平面,因为平面,所以平面平面;
(2)因为底面中,,,侧面为等边三角形,是的中点,所以,,,,因为平面,,平面,所以,,所以,
因为,所以,所以,
设点,到平面的距离分别为,,因为,所以,
,解得,因为三棱锥的体积为,
所以,所以,解得,所以,所以,因为,所以,取靠近点的四等份点,连接,则,因为平面,所以平面,因为平面,所以,过点作于,连接,因为,所以平面,因为平面,所以,所以为二面角的平面角,因为,所以,
因为,所以四边形为矩形,所以,
所以在中,,所以二面角的正切值为
22.【详解】(1),,,
,
,所以,
(2)“平板车要想顺利通过直角走廊”即对任意角,平板车的长度,
记,则,又则,
所以,所以,即,则,
记,,则,函数
因为,在上都递增,所以在上都递增,
所以在上的单调递减;当时取得最小值.所以长度不能超过米
同课章节目录
