18.1.2平行四边形的判定 第二课时 课件(38张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定 第二课时 课件(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-16 17:32:07 | ||
图片预览






文档简介
(共38张PPT)
第十八章 平行四边形
18.1.2平行四边形的判定
第二课时
1. 理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
平行四边形的判定方法及应用.
平行四边形的判定定理与性质定理的灵活应用.
【学习目标】
【学习重点】
【学习难点】
复习旧知 引入新课
平形四边形的判定
两组对边分别平行的四边形是平行四边形;
边
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形.
角
温故知新
回忆平行四边形的判定定理:
平行四边形的对角线互相平分.
对角线的性质:
逆命题:
对角线互相平分的四边形是平行四边形.
合作交流 探索新知
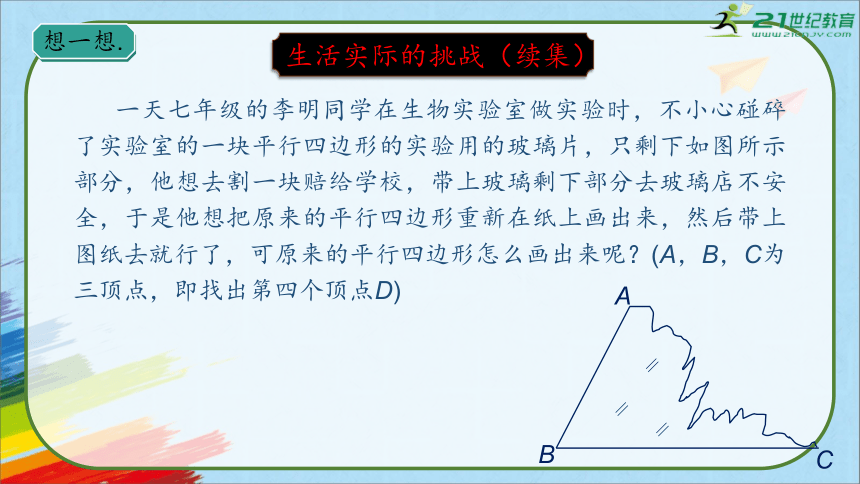
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战(续集)
想一想.
A
B
C
O
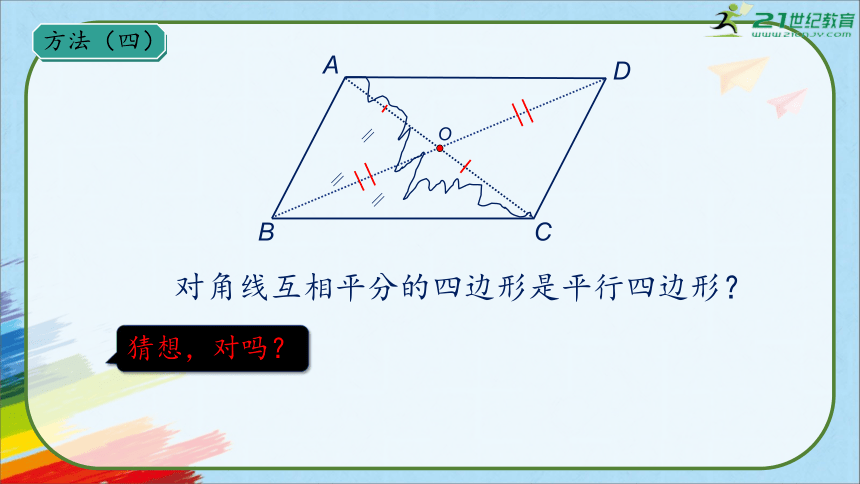
对角线互相平分的四边形是平行四边形?
方法(四)
D
A
B
C
猜想,对吗?
2
O
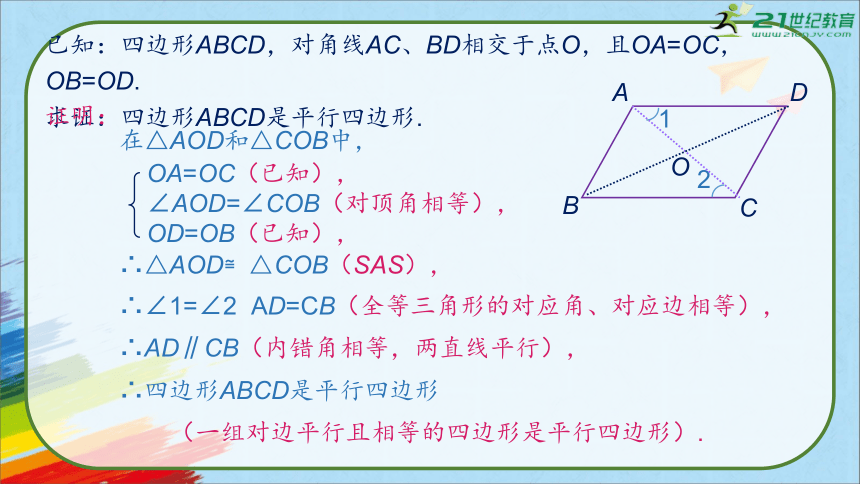
已知:四边形ABCD,对角线AC、BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOD和△COB中,
OA=OC(已知),
∠AOD=∠COB(对顶角相等),
OD=OB(已知),
∴△AOD≌△COB(SAS),
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等),
∴AD∥CB(内错角相等,两直线平行),
∴四边形ABCD是平行四边形
B
A
C
1
D
(一组对边平行且相等的四边形是平行四边形).
对角线互相平分的四边形是平行四边形.
符号语言:
A
B
C
D
O
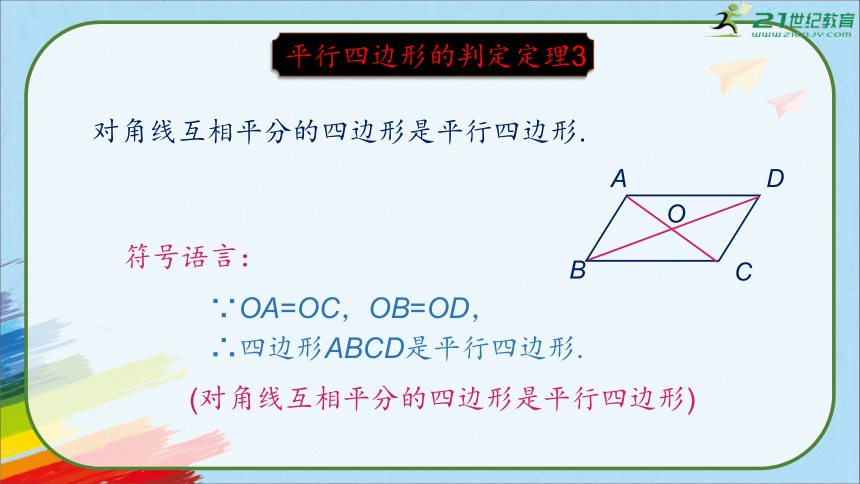
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
(对角线互相平分的四边形是平行四边形)
平行四边形的判定定理3
方法(五)
A
B
C
D
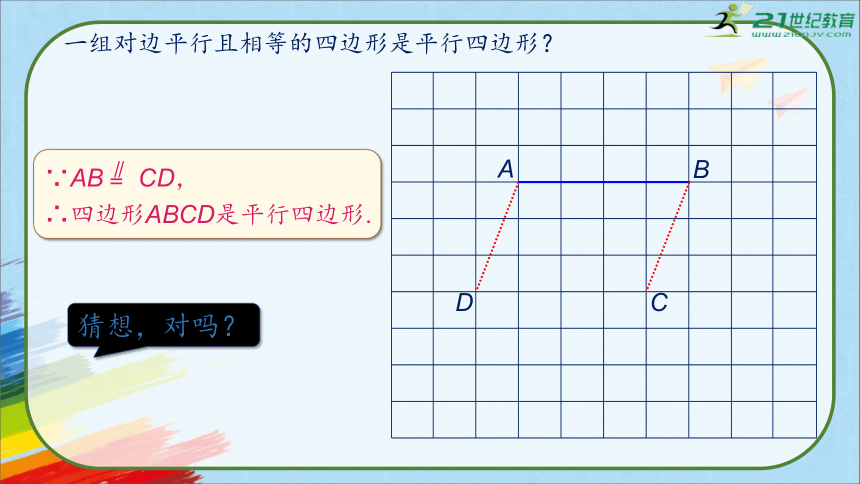
一组对边平行且相等的四边形是平行四边形?
∵AB CD,
∴四边形ABCD是平行四边形.
﹦
∥
猜想,对吗?
A
B
C
D
A
B
C
D
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AD∥BC,
∴∠DAC=∠ACB,
又∵AD=BC,AC=CA,
∴ΔABC≌ΔCDA,
∴∠BAC=∠ACD,
∴AB∥CD,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
已知:在四边形ABCD中, AD BC.
﹦
∥
一组对边平行且相等的四边形是平行四边形.
符号语言:
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
平行四边形的判定定理4
A
B
C
D
∵AB CD,
﹦
∥
应用迁移 巩固提高
例1:如图,已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF.
D
O
A
B
C
E
F
证明:
连对角线BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AE=CF,
∴AO-AE=CO-CF 即EO=FO,
又BO=DO,
∴四边形BFDE是平行四边形.
求证:四边形BFDE是平行四边形.
例2:如图,在平行四边形ABCD中,E、F分别是边BC和AD上
的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
证明:
∵四边形ABCD是平行四边形
∴AD∥BC
即AF∥CE
又∵AF = CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
你还有其他方法吗?
可求得△ABE≌△CDF(SAS),
∴AE=CF,
又∵AF=CE,
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形).
例3: □ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点.四边形EFGH是平行四边形吗?为什么?
G
E
F
D
O
H
C
B
A
解:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴OE= OA,OG= OC,OF= OB,
OH= OD.
∴OE=OG,OF=OH.
∴四边形EFGH是平行四边形.
随堂练习 巩固新知
1.下列说法不能判断平行四边形是( )
A.一组对边平行且相等
B.一组对边平行,一组对角相等
C.一组对边相等,一组对角相等
D.两组对边相等
2.给四边形ABCD添加条件,使之成为平行四边形,下面添加的条件不能得到四边形ABCD是平行四边形的是( )
A.AB=CD,AB∥CD B.AB∥CD,AD=BC
C.AB=CD,AD=BC D.AC与BD相互平分
C
B
3.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
A
A
B
C
D
O
4.已知:如图,E,F分别是□ABCD的边AD,BC的中点.
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义),
AD=BC (平行四边形的对边分别相等) ,
∵E,F分别是AD,BC的中点,
∴四边形EBFD是平行四边形.
(一组对边平行并且相等的四边形是平行四边形).
∴BE=DF (平行四边形的对边分别相等).
∴ED=BF,即ED BF.
﹦
∥
证明:
∵四边形ABCD是平行四边形.
∴OA=OC,AD//BC,
∴∠AEF=∠CFE,
又∵∠AOE=∠COF,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AECF是平行四边形.
D
F
E
C
B
A
O
5.如下图, ABCD的对角线AC,BD相交于O,EF过点O与AD,
BC分别相交于点E,F.连接EB,EC.
求证:四边形AECF是平行四边形.
当堂检测 及时反馈
1.四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.4组 B.3组 C.2组 D.1组
B
A
B
C
D
O
2.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC D.AB=CD,AO=CO
D
A
B
C
D
O
3.如图,在△ABC中,点D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,下列说法错误的是( )
A.△ABD≌△ECD
B.连接BE,四边形ABEC为平行四边形
C.DA=DE
D.CE=CA
D
4.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形.
BO=DO
A
B
C
D
O
5.如图,在平行四边形ABCD中,对角线AC、BD交于点O,点E、F在BD上,请你添加一个条件 使四边形AECF是平行四边形(填加一个即可).
BE=DF或OE=OF
A
B
C
D
O
E
F
6.如图,四边形ABCD中,∠A=∠ABC=90°,点E是边CD上一点,连接BE,并延长与AD的延长线相交于点F,请你只添加一个条件: ,使四边形BDFC为平行四边形.
BC=DF
A
B
F
D
E
C
7.已知:如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,
DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.
证明:
∵DF∥BE,
∴∠DFC = ∠BEA,
∴∠AFD = 180°-∠DFC
= 180°-∠BEA = ∠BEC,
又∵ AF = CE,DF = BE,
∴△AFD≌△CEB,
∴AD = BC, ∠DAF = ∠BCE,
∴AD // BC,
∴四边形ABCD是平行四边形.
D
C
B
A
F
E
7.已知:如图,E,F是□ABCD的对角线BD上的两点,且
∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
A
B
C
D
E
F
O
证明:
连结AC,交BD于点O,
∵AB∥CD
在□ABCD中,BO=DO,AO=CO,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,AB=CD,
∴△ABE≌△CDF,
∴BE=DF,
∴BO-BE=DO-DF,即EO=FO,
∴四边形AECF是平行四边形.
(平行四边形的对角线互相平分)
(平行四边形的定义),
(对角线互相平分的四边形是平行四边形)
拓展延伸 能力提升
1.如图,平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n)其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
(5,3)或(1,﹣3)
O
A
B
x
y
C(5,3)
C(1,-3)
O→B坐标平移变化:
横坐标+3
纵坐标不变
A→O坐标平移变化:
横坐标-2
纵坐标-3
(2,3)
(3,0)
任意画一个三角形和三角形一边上的中线.比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么 再画几个三角形试一试,你发现的规律仍然成立吗 试证明你的发现.
探究活动
E
D
C
B
A
发现:三角形一条边上的中线的2倍小于另两条边的和.
E
2.已知:如图,AD是⊿ABC的中线,
求证:2AD < AB + AC.
证明:
如图,延长AD至E,使ED = AD.连结BE,EC.
∵BD = CD,
∴四边形ABEC是平行四边形
(对角线互相平分的四边形是平行四边形).
∴AB = CE(平行四边形的两组对边分别相等).
∵AC + CE > AE,
∴AB+AC > 2AD,
即2AD < AB + AC.
D
C
B
A
总结反思 知识内化
对角线互相平分的四边形是平行四边形.
小 结
判定一个四边形是平行四边形可从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑
从边
考虑
两组对角分别相等的四边形是平行四边形.
从对角线考虑
第十八章 平行四边形
18.1.2平行四边形的判定
第二课时
1. 理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
平行四边形的判定方法及应用.
平行四边形的判定定理与性质定理的灵活应用.
【学习目标】
【学习重点】
【学习难点】
复习旧知 引入新课
平形四边形的判定
两组对边分别平行的四边形是平行四边形;
边
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形.
角
温故知新
回忆平行四边形的判定定理:
平行四边形的对角线互相平分.
对角线的性质:
逆命题:
对角线互相平分的四边形是平行四边形.
合作交流 探索新知
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战(续集)
想一想.
A
B
C
O
对角线互相平分的四边形是平行四边形?
方法(四)
D
A
B
C
猜想,对吗?
2
O
已知:四边形ABCD,对角线AC、BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOD和△COB中,
OA=OC(已知),
∠AOD=∠COB(对顶角相等),
OD=OB(已知),
∴△AOD≌△COB(SAS),
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等),
∴AD∥CB(内错角相等,两直线平行),
∴四边形ABCD是平行四边形
B
A
C
1
D
(一组对边平行且相等的四边形是平行四边形).
对角线互相平分的四边形是平行四边形.
符号语言:
A
B
C
D
O
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
(对角线互相平分的四边形是平行四边形)
平行四边形的判定定理3
方法(五)
A
B
C
D
一组对边平行且相等的四边形是平行四边形?
∵AB CD,
∴四边形ABCD是平行四边形.
﹦
∥
猜想,对吗?
A
B
C
D
A
B
C
D
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AD∥BC,
∴∠DAC=∠ACB,
又∵AD=BC,AC=CA,
∴ΔABC≌ΔCDA,
∴∠BAC=∠ACD,
∴AB∥CD,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
已知:在四边形ABCD中, AD BC.
﹦
∥
一组对边平行且相等的四边形是平行四边形.
符号语言:
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
平行四边形的判定定理4
A
B
C
D
∵AB CD,
﹦
∥
应用迁移 巩固提高
例1:如图,已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF.
D
O
A
B
C
E
F
证明:
连对角线BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AE=CF,
∴AO-AE=CO-CF 即EO=FO,
又BO=DO,
∴四边形BFDE是平行四边形.
求证:四边形BFDE是平行四边形.
例2:如图,在平行四边形ABCD中,E、F分别是边BC和AD上
的两点,且AF=CE.
求证:四边形AECF为平行四边形.
B
A
C
D
F
E
证明:
∵四边形ABCD是平行四边形
∴AD∥BC
即AF∥CE
又∵AF = CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
你还有其他方法吗?
可求得△ABE≌△CDF(SAS),
∴AE=CF,
又∵AF=CE,
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形).
例3: □ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点.四边形EFGH是平行四边形吗?为什么?
G
E
F
D
O
H
C
B
A
解:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴OE= OA,OG= OC,OF= OB,
OH= OD.
∴OE=OG,OF=OH.
∴四边形EFGH是平行四边形.
随堂练习 巩固新知
1.下列说法不能判断平行四边形是( )
A.一组对边平行且相等
B.一组对边平行,一组对角相等
C.一组对边相等,一组对角相等
D.两组对边相等
2.给四边形ABCD添加条件,使之成为平行四边形,下面添加的条件不能得到四边形ABCD是平行四边形的是( )
A.AB=CD,AB∥CD B.AB∥CD,AD=BC
C.AB=CD,AD=BC D.AC与BD相互平分
C
B
3.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
A
A
B
C
D
O
4.已知:如图,E,F分别是□ABCD的边AD,BC的中点.
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义),
AD=BC (平行四边形的对边分别相等) ,
∵E,F分别是AD,BC的中点,
∴四边形EBFD是平行四边形.
(一组对边平行并且相等的四边形是平行四边形).
∴BE=DF (平行四边形的对边分别相等).
∴ED=BF,即ED BF.
﹦
∥
证明:
∵四边形ABCD是平行四边形.
∴OA=OC,AD//BC,
∴∠AEF=∠CFE,
又∵∠AOE=∠COF,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AECF是平行四边形.
D
F
E
C
B
A
O
5.如下图, ABCD的对角线AC,BD相交于O,EF过点O与AD,
BC分别相交于点E,F.连接EB,EC.
求证:四边形AECF是平行四边形.
当堂检测 及时反馈
1.四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.4组 B.3组 C.2组 D.1组
B
A
B
C
D
O
2.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC D.AB=CD,AO=CO
D
A
B
C
D
O
3.如图,在△ABC中,点D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,下列说法错误的是( )
A.△ABD≌△ECD
B.连接BE,四边形ABEC为平行四边形
C.DA=DE
D.CE=CA
D
4.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形.
BO=DO
A
B
C
D
O
5.如图,在平行四边形ABCD中,对角线AC、BD交于点O,点E、F在BD上,请你添加一个条件 使四边形AECF是平行四边形(填加一个即可).
BE=DF或OE=OF
A
B
C
D
O
E
F
6.如图,四边形ABCD中,∠A=∠ABC=90°,点E是边CD上一点,连接BE,并延长与AD的延长线相交于点F,请你只添加一个条件: ,使四边形BDFC为平行四边形.
BC=DF
A
B
F
D
E
C
7.已知:如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,
DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.
证明:
∵DF∥BE,
∴∠DFC = ∠BEA,
∴∠AFD = 180°-∠DFC
= 180°-∠BEA = ∠BEC,
又∵ AF = CE,DF = BE,
∴△AFD≌△CEB,
∴AD = BC, ∠DAF = ∠BCE,
∴AD // BC,
∴四边形ABCD是平行四边形.
D
C
B
A
F
E
7.已知:如图,E,F是□ABCD的对角线BD上的两点,且
∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
A
B
C
D
E
F
O
证明:
连结AC,交BD于点O,
∵AB∥CD
在□ABCD中,BO=DO,AO=CO,
∴∠ABE=∠CDF,
又∵∠BAE=∠DCF,AB=CD,
∴△ABE≌△CDF,
∴BE=DF,
∴BO-BE=DO-DF,即EO=FO,
∴四边形AECF是平行四边形.
(平行四边形的对角线互相平分)
(平行四边形的定义),
(对角线互相平分的四边形是平行四边形)
拓展延伸 能力提升
1.如图,平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n)其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
(5,3)或(1,﹣3)
O
A
B
x
y
C(5,3)
C(1,-3)
O→B坐标平移变化:
横坐标+3
纵坐标不变
A→O坐标平移变化:
横坐标-2
纵坐标-3
(2,3)
(3,0)
任意画一个三角形和三角形一边上的中线.比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么 再画几个三角形试一试,你发现的规律仍然成立吗 试证明你的发现.
探究活动
E
D
C
B
A
发现:三角形一条边上的中线的2倍小于另两条边的和.
E
2.已知:如图,AD是⊿ABC的中线,
求证:2AD < AB + AC.
证明:
如图,延长AD至E,使ED = AD.连结BE,EC.
∵BD = CD,
∴四边形ABEC是平行四边形
(对角线互相平分的四边形是平行四边形).
∴AB = CE(平行四边形的两组对边分别相等).
∵AC + CE > AE,
∴AB+AC > 2AD,
即2AD < AB + AC.
D
C
B
A
总结反思 知识内化
对角线互相平分的四边形是平行四边形.
小 结
判定一个四边形是平行四边形可从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑
从边
考虑
两组对角分别相等的四边形是平行四边形.
从对角线考虑
