2022—2023学年北师大版七年级数学下册 第六章 概率初步单元自测题 (含解析)
文档属性
| 名称 | 2022—2023学年北师大版七年级数学下册 第六章 概率初步单元自测题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-18 21:19:47 | ||
图片预览




文档简介
北师大版七年级数学下册第六章 概率初步 单元自测题
一、单选题
1.下列事件中,是必然事件的是( )
A.不共线的三条线段可以组成一个三角形 B.400人中有两个人的生日在同一天
C.早上的太阳从西方升起 D.打开电视机,它正在播放动画
2.下列事件是随机事件的是( )
A.打开电视,正在播放《中国机长》 B.白发三千丈,缘愁似个长
C.离离原上草,一岁一枯荣 D.钝角三角形的内角和大于
3.下列说法正确的是( )
A.“经过有交通信号的路口遇到红灯”是必然事件
B.已知某篮球运动员投篮投中的概率为,则他投次一定可投中7次
C.明天太阳从东方升起是随机事件
D.投掷一枚硬币正面朝上是随机事件
4.一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在80%左右,则a的值约为( )
A.9 B.12 C.15 D.18
5.如图,在正六边形转盘中,有两个正三角形涂有阴影,为可绕点O自由转动的指针,转动指针(若指针恰好停在分界线上,则重新转动),指针落在有阴影的区域内的概率为( )
A. B. C. D.
6.在“石头、剪刀、布”游戏中,对方出“剪刀”.这个事件是( )
A.必然事件 B.随机事件 C.不可能事件 D.确定性事件
7.已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是( )
A.通过抛一枚均匀硬币确定篮球赛中谁先发球是公平的
B.大量重复抛一枚均匀硬币,出现正面朝上的频率稳定于
C.连续抛一枚均匀硬币10次可能都是正面朝上
D.连续抛一枚均匀硬币2次必有1次正面朝上
8.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,并绘制了如下表格.则该结果发生的概率约为( )
实验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.345 0.339 0.333
A. B. C. D.
9.有五张背面完全相同的卡片,正面分别写有数字1,2,3,4,5,把这些卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是奇数的概率为( )
A. B. C. D.
10.一个不透明的袋子里装有2个红球和4个白球,它们除颜色外其余都相同,从袋中任意摸出一个球是白球的概率为( )
A. B. C. D.
二、填空题
11.将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人,已知甲有5张红桃牌,乙有4张红桃牌,那么丁的红桃牌有 种不同的情况.
12.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:
移植总次数n 1500 3500 7000 9000 14000
成活数m 1335 3203 6335 8037 12628
成活的频率
估计该种幼树在此条件下移植成活的概率是 (结果精确到0.1).
13.在一个不透明的口袋中装有红、黄两种颜色的球,它们形状大小完全相同,其中5个红球,若干个黄球,从中随机摸出一个球,记下颜色后放回,重复以上过程,经过多次试验发现摸到红球的频率稳定在0.2,据此估计袋中黄球的个数约为 个.
14.有背面完全相同,正面写有“十九届六中全会”字样的卡片n张,“元宇宙”字样的卡片4张,现正面朝下放置在桌面上,将其混合后,从中随机抽取一张,若抽中“十九届六中全会”字样的卡片的概率为,则 .
三、解答题
15.一盒乒乓球中共有6只,其中2只次品,4只正品,正品和次品大小和形状完全相同,每次任取3只,出现了下列事件:(1)3只正品;(2)至少有一只次品;(3)3只次品;(4)至少有一只正品
指出这些事件分别是什么事件.
16.某封闭的纸箱中有红色、黄色的玻璃球若干,为了估计出纸箱中红色、黄色球的数目,小亮向纸箱中放入25个白球,通过多次摸球实验后,发现摸到白球的频率为25%,摸到黄球的频率为40%,试估计出原纸箱中红球、黄球的数目.
17.净月某校在抗疫期间组织志愿小组到附近敬老院为老人服务,准备从初三(1)班中的3名男生小亮、小明、小伟和2名女生小红、小丽中选取一名男生和一名女生.请用画树状图(或列表)的方法,求出恰好选中男生小明和女生小红的概率.
四、综合题
18.为了解某校八年级全体女生“仰卧起坐”项目的成绩,随机抽取了部分女生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制成如下不完整的统计图、表.
根据以上信息解答下列问题:
(1)a= ,b= ,表示A等级扇形的圆心角的度数为 度;
(2)A等级中有八年级(5)班两名学生,如果要从A等级学生中随机选取一名介绍“仰卧起坐”锻炼经验,求抽到八年级(5)班学生的可能性大小.
19.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的频率
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.01)
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
20.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
实验种子数 (粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数 0 4 45 92 188 476 951 1900 2850
(1)估计该麦种的发芽概率.
(2)如果播种该种小麦每公顷所需麦苗数为4000000棵,种子发芽后的成秧率为80%,该麦种的千粒质量为50g.那么播种3公顷该种小麦,估计约需麦种多少千克(精确到1kg)?
21.某同学拿出四张扑克牌,它们的牌面数字分别为1,3,4,4,其他全都相同,将这四张扑克牌背面朝上洗匀.
(1)若随机抽取一张扑克牌,抽到数字4的概率为 ;
(2)将这四张扑克牌背面朝上洗匀,从中随机抽取一张,不放回;再从剩余的三张牌中随机抽取一张,请利用列表法或画树状图法,求抽取的这两张牌的牌面数字之和小于6的概率.
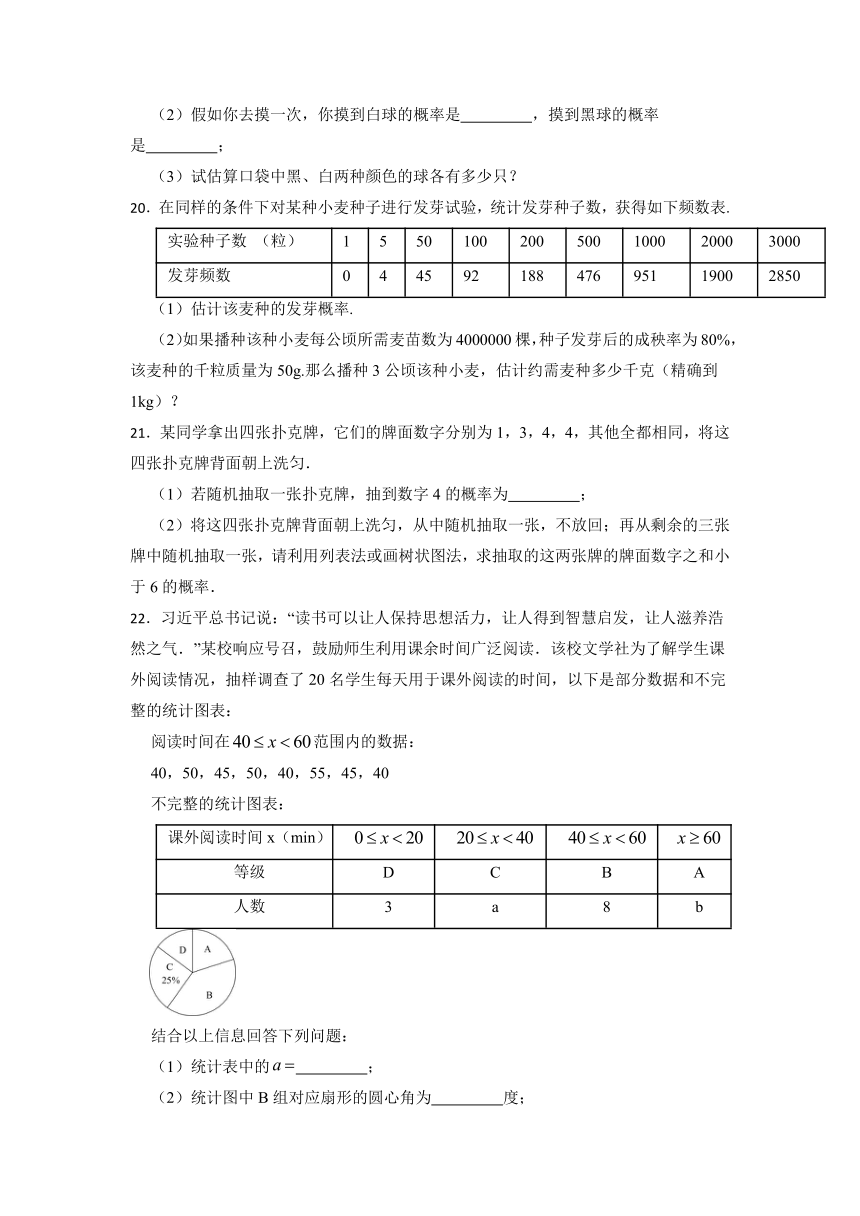
22.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了20名学生每天用于课外阅读的时间,以下是部分数据和不完整的统计图表:
阅读时间在范围内的数据:
40,50,45,50,40,55,45,40
不完整的统计图表:
课外阅读时间x(min)
等级 D C B A
人数 3 a 8 b
结合以上信息回答下列问题:
(1)统计表中的 ;
(2)统计图中B组对应扇形的圆心角为 度;
(3)阅读时间在范围内的数据的众数是 ;调查的20名同学课外阅读时间的中位数是 ;
(4)根据调查结果,请你估计全校800名同学课外阅读时间不少于的人数.
答案解析部分
1.【答案】B
【解析】【解答】解:A选项中不共线的三条线段不一定首尾相接,不一定组成三角形,是随机事件;
B选项中一年最多366天,则400人中至少有2人生日在同一天,是必然事件;
C选项中太阳从西方升起是不可能事件;
D选项中打开电视不一定播放动画片,是随机事件;
故答案为:B
【分析】必然事件是指一定会发生或一定不会发生的事件;随机事件是指可能发生也可能不发生的事件.根据定义并结合各选项即可判断求解.
2.【答案】A
【解析】【解答】解:A、打开电视,正在播放《中国机长》,是随机事件,符合题意,选项正确;
B、白发三千丈,缘愁似个长,是不可能事件,不符合题意,选项错误;
C、离离原上草,一岁一枯荣,是必然事件,不符合题意,选项错误;
D、钝角三角形的内角和大于,是不可能事件,不符合题意,选项错误.
故答案为:A.
【分析】在一定条件下,可能发生,也可能不会发生的事件就是随机事件;在一定条件下,一定不会发生的事件就是不可能事件;在一定条件下,一定会发生的事件就是必然事件,根据定义即可一一判断得出答案.
3.【答案】D
【解析】【解答】解:A. “经过有交通信号的路口遇到红灯”是随机事件,故该选项不正确,不符合题意;
B. 已知某篮球运动员投篮投中的概率为,则他投次有可能可投中7次,故该选项不正确,不符合题意;
C. 明天太阳从东方升起是必然事件,故该选项不正确,不符合题意;
D. 投掷一枚硬币正面朝上是随机事件,故该选项正确,符合题意.
故答案为:D.
【分析】根据随机事件及概率的意义逐一判断即可.
4.【答案】B
【解析】【解答】解:由题意可得,×100%=80%,
解得,a=12.
故答案为:B.
【分析】利用白球的个数÷小球的总个数×100%=80%进行计算即可.
5.【答案】B
【解析】【解答】解:根据题意得:指针落在有阴影的区域内的概率为.
故答案为:B
【分析】利用几何概率公式的计算方法求解即可。
6.【答案】B
【解析】【解答】解:对方出“剪刀”.这个事件是是随机事件.
故答案为:B.
【分析】必然事件:在条件S下,一定会发生的事件,叫做相对条件S的必然事件,简称必然[
不可能事件:在条件S下,一定不可能发生的事件,叫做相对条件S的不可能事件,简称不可能事件;
随机事件:随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件.
7.【答案】D
【解析】【解答】解:抛一枚均匀硬币正面朝上的概率为,就是经过大量重复的实验,抛一枚均匀硬币正面朝上的频率越稳定在左右,因此,
A.通过抛一枚均匀硬币确定篮球赛中谁先发球是公平的,这是公平的,因此选项A不符合题意;
B.大量重复抛一枚均匀硬币,出现正面朝上的频率稳定于,这种说法是正确的,因此选项B不符合题意;
C.连续抛一枚均匀硬币10次可能都是正面朝上,是可能存在的,因此选项C不符合题意;
D.连续抛一枚均匀硬币2次必有1次正面朝上,这是不正确的,因此选项D符合题意;
故答案为:D.
【分析】根据概率的意义可判断A;根据频率估计概率的知识可判断B;根据随机事件的概念可判断C、D.
8.【答案】B
【解析】【解答】解:由表格数据,可知某一结果发生的概率约为0.33,
∵,,,,
∴与最接近的是,
∴该结果发生的概率约为.
故答案为:B
【分析】利用频率估算概率的计算方法求解即可。
9.【答案】B
【解析】【解答】解:由题意可知一共有5个数,奇数有3个,
∴P(抽取一张,其正面的数字是奇数)=.
故答案为:B
【分析】利用已知条件可得到所有等可能的结果数及从中随机抽取一张,其正面的数字是奇数的情况数,然后利用概率公式进行计算.
10.【答案】A
【解析】【解答】解:由题意可得:白球的个数为4,球的总数为6,
∴摸到白球的概率为.
故答案为:A.
【分析】利用白球的个数除以球的总数即可求出对应的概率.
11.【答案】5
【解析】【解答】解:∵一副扑克牌有13张红桃,甲有5张红桃牌,乙有4张红桃牌,
∴剩余4张红桃,
∴丁的红桃牌有0,1,2,3,4张五种不同的情况.
故答案为:5.
【分析】一副扑克牌有13张红桃,利用已知可得到剩余4张红桃,据此可得到丁的红桃牌的数量的不同情况.
12.【答案】0.9
【解析】【解答】解:由表可知:经过大量重复试验,成活的频率逐渐稳定到0.9,
∴该种幼树在此条件下移植成活的概率是0.9,
故答案为:0.9.
【分析】由表可知:经过大量重复试验,成活的频率逐渐稳定到0.9,然后根据频率估计概率的知识进行解答.
13.【答案】20
【解析】【解答】解:设估计袋中黄球的个数约为x个,根据题意得
解之:x=20.
故答案为:20
【分析】设估计袋中黄球的个数约为x个,根据经过多次试验发现摸到红球的频率稳定在0.2,可得到关于x的方程,解方程求出x的值.
14.【答案】16
【解析】【解答】解:∵抽中“十九届六中全会”字样的卡片的概率为,
∴,
解得n=16.
故答案为:16.
【分析】根据概率公式结合题意可得,求解即可.
15.【答案】解:(1),(2)可能发生,也可能不发生,是随机事件.
(3)一定不会发生,是不可能事件.
(4)一定发生,是必然事件.
【解析】【分析】根据正品、次品的只数可得:取出的3只可能为3只正品;也可能为1只次品、2只正品;2只次品,1只正品;根据次品的只数可知不可能取出3只次品;根据次品只数为2只可知一定会取出正品,据此解答.
16.【答案】解:由概率和频率公式可求得纸箱中国球的总数和红、白球的数目。如:
球总数=白球数目/白球频率=2525%=100 个
黄球数目=黄球频率球总数=40%100=40 个
红球数目=球总数-白球数目-黄球数目=100-25-40=35 个
则此题求得纸箱中红球35个,黄球40个。
【解析】【分析】本题若想求得红、黄球的数目,则需要先利用白球求出纸箱中的总球数,最后再求得红球和白球数目。
17.【答案】解:列表得:
小亮 小明 小伟
小丽 小丽,小亮 小丽,小明 小丽,小伟
小红 小红,小亮 小红,小明 小红,小伟
∵共有6种等可能的情况,而正好是男生小明和女生小红的有1种情况,
∴正好抽到男生小明和女生小红的概率= .
【解析】【分析】列表可确定共有6种情况,而正好是男生小明和女生小红的有1种情况,根据概率公式求解即可.
18.【答案】(1)10;40;90
(2)解:抽到八年级(5)班学生的可能性大小为:
【解析】【解答】解:(1)随机抽女生人数:4÷10%=40(名),即b=40;
A等级人数:40-24-4-2=10(名),即a=10;
扇形图中表示A的圆心角的度数360°× =90°
故答案为:10,40,90;
【分析】(1)根据C等级的人数和所占比例可知随机抽女生人数:4÷10%=40(名),即b=40;A等级人数:40-24-4-2=10(名),即a=10;扇形图中表示A的圆心角的度数360°× =90°;(2)根据概率公式求解即可.
19.【答案】(1)0.60
(2)0.6;0.4
(3)解:因为摸到白球的概率是0.6,摸到黑球的概率是0.4,
所以口袋中黑、白两种颜色的球有:
白球是只,
黑球是只.
答:估计口袋中白色的球有12只,黑色的球有8只.
【解析】【解答】解:(1)解:根据题意可得当很大时,摸到白球的频率将会接近0.60;
故答案为:0.60;
(2)解:因为当很大时,摸到白球的频率将会接近0.60;
所以摸到白球的概率是0.6;
摸到黑球的概率是0.4;
故答案为:0.6,0.4;
【分析】(1)根据表格中的信息可知:当n很大时,摸到白球的频率将会接近0.60;
(2)结合(1)的结论并根据用频率估计概率可求解;
(3)根据频数=概率×样本容量可求解.
20.【答案】(1)解:根据实验数量变大,发芽数也在增大,2850÷3000×100%=95%,
故该麦种的发芽概率约为95%;
(2)解:设约需麦种x千克,
x×1000÷50×1000×95%×80%=4000000×3,
化简得15200x=12000000,
解得x=789,
答:约需麦种790千克
【解析】【分析】(1)在大量的实验的前提下,用发芽频数除以实验种子数即可;
(2) 设约需麦种x千克, 根据麦种的粒数× 发芽概率 × 成秧率 =4000000×3,列出方程解之即可.
21.【答案】(1)
(2)解:
此事件共有12种情况,且可能性相等,其中抽取的这两张牌的牌面数字之和小于6的有6种情况,
∴
【解析】【解答】解:(1) 若随机抽取一张扑克牌,抽到数字4的概率为:,
故答案为:.
【分析】(1)根据概率公式计算求解即可;
(2)先画树状图,再求出此事件共有12种情况,且可能性相等,其中抽取的这两张牌的牌面数字之和小于6的有6种情况,最后求概率即可。
22.【答案】(1)5
(2)144
(3)40;40
(4)解:根据题意得:,
∴全校800名同学课外阅读时间不少于的人数为人.
【解析】【解答】(1)解:根据题意得:;
故答案为:5
(2)解:B组对应扇形的圆心角为;
故答案为:144
(3)解:阅读时间在范围内的数据中,40出现的次数最多,
∴阅读时间在范围内的数据的众数是;
把阅读时间在范围内的数据从小到大排列为:40,40,40,45,45,50, 50, 55,
∵,
∴调查的20名同学课外阅读时间位于正中间的两个数分别为40,40,
∴调查的20名同学课外阅读时间的中位数是;
故答案为:40;40
【分析】(1)用样本容量乘25%可得a的值,再用样本容量分别减去其他等级的频数可得b的值;
(2)用360°乘B等级所占比例即可;
(3)分别根据众数和中位数的定义解答即可;
(4)用800乘样本中课外阅读时间不少于40min的人数所占比例即可.
一、单选题
1.下列事件中,是必然事件的是( )
A.不共线的三条线段可以组成一个三角形 B.400人中有两个人的生日在同一天
C.早上的太阳从西方升起 D.打开电视机,它正在播放动画
2.下列事件是随机事件的是( )
A.打开电视,正在播放《中国机长》 B.白发三千丈,缘愁似个长
C.离离原上草,一岁一枯荣 D.钝角三角形的内角和大于
3.下列说法正确的是( )
A.“经过有交通信号的路口遇到红灯”是必然事件
B.已知某篮球运动员投篮投中的概率为,则他投次一定可投中7次
C.明天太阳从东方升起是随机事件
D.投掷一枚硬币正面朝上是随机事件
4.一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在80%左右,则a的值约为( )
A.9 B.12 C.15 D.18
5.如图,在正六边形转盘中,有两个正三角形涂有阴影,为可绕点O自由转动的指针,转动指针(若指针恰好停在分界线上,则重新转动),指针落在有阴影的区域内的概率为( )
A. B. C. D.
6.在“石头、剪刀、布”游戏中,对方出“剪刀”.这个事件是( )
A.必然事件 B.随机事件 C.不可能事件 D.确定性事件
7.已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是( )
A.通过抛一枚均匀硬币确定篮球赛中谁先发球是公平的
B.大量重复抛一枚均匀硬币,出现正面朝上的频率稳定于
C.连续抛一枚均匀硬币10次可能都是正面朝上
D.连续抛一枚均匀硬币2次必有1次正面朝上
8.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,并绘制了如下表格.则该结果发生的概率约为( )
实验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.345 0.339 0.333
A. B. C. D.
9.有五张背面完全相同的卡片,正面分别写有数字1,2,3,4,5,把这些卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是奇数的概率为( )
A. B. C. D.
10.一个不透明的袋子里装有2个红球和4个白球,它们除颜色外其余都相同,从袋中任意摸出一个球是白球的概率为( )
A. B. C. D.
二、填空题
11.将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人,已知甲有5张红桃牌,乙有4张红桃牌,那么丁的红桃牌有 种不同的情况.
12.某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:
移植总次数n 1500 3500 7000 9000 14000
成活数m 1335 3203 6335 8037 12628
成活的频率
估计该种幼树在此条件下移植成活的概率是 (结果精确到0.1).
13.在一个不透明的口袋中装有红、黄两种颜色的球,它们形状大小完全相同,其中5个红球,若干个黄球,从中随机摸出一个球,记下颜色后放回,重复以上过程,经过多次试验发现摸到红球的频率稳定在0.2,据此估计袋中黄球的个数约为 个.
14.有背面完全相同,正面写有“十九届六中全会”字样的卡片n张,“元宇宙”字样的卡片4张,现正面朝下放置在桌面上,将其混合后,从中随机抽取一张,若抽中“十九届六中全会”字样的卡片的概率为,则 .
三、解答题
15.一盒乒乓球中共有6只,其中2只次品,4只正品,正品和次品大小和形状完全相同,每次任取3只,出现了下列事件:(1)3只正品;(2)至少有一只次品;(3)3只次品;(4)至少有一只正品
指出这些事件分别是什么事件.
16.某封闭的纸箱中有红色、黄色的玻璃球若干,为了估计出纸箱中红色、黄色球的数目,小亮向纸箱中放入25个白球,通过多次摸球实验后,发现摸到白球的频率为25%,摸到黄球的频率为40%,试估计出原纸箱中红球、黄球的数目.
17.净月某校在抗疫期间组织志愿小组到附近敬老院为老人服务,准备从初三(1)班中的3名男生小亮、小明、小伟和2名女生小红、小丽中选取一名男生和一名女生.请用画树状图(或列表)的方法,求出恰好选中男生小明和女生小红的概率.
四、综合题
18.为了解某校八年级全体女生“仰卧起坐”项目的成绩,随机抽取了部分女生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制成如下不完整的统计图、表.
根据以上信息解答下列问题:
(1)a= ,b= ,表示A等级扇形的圆心角的度数为 度;
(2)A等级中有八年级(5)班两名学生,如果要从A等级学生中随机选取一名介绍“仰卧起坐”锻炼经验,求抽到八年级(5)班学生的可能性大小.
19.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的频率
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.01)
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
20.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
实验种子数 (粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数 0 4 45 92 188 476 951 1900 2850
(1)估计该麦种的发芽概率.
(2)如果播种该种小麦每公顷所需麦苗数为4000000棵,种子发芽后的成秧率为80%,该麦种的千粒质量为50g.那么播种3公顷该种小麦,估计约需麦种多少千克(精确到1kg)?
21.某同学拿出四张扑克牌,它们的牌面数字分别为1,3,4,4,其他全都相同,将这四张扑克牌背面朝上洗匀.
(1)若随机抽取一张扑克牌,抽到数字4的概率为 ;
(2)将这四张扑克牌背面朝上洗匀,从中随机抽取一张,不放回;再从剩余的三张牌中随机抽取一张,请利用列表法或画树状图法,求抽取的这两张牌的牌面数字之和小于6的概率.
22.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读.该校文学社为了解学生课外阅读情况,抽样调查了20名学生每天用于课外阅读的时间,以下是部分数据和不完整的统计图表:
阅读时间在范围内的数据:
40,50,45,50,40,55,45,40
不完整的统计图表:
课外阅读时间x(min)
等级 D C B A
人数 3 a 8 b
结合以上信息回答下列问题:
(1)统计表中的 ;
(2)统计图中B组对应扇形的圆心角为 度;
(3)阅读时间在范围内的数据的众数是 ;调查的20名同学课外阅读时间的中位数是 ;
(4)根据调查结果,请你估计全校800名同学课外阅读时间不少于的人数.
答案解析部分
1.【答案】B
【解析】【解答】解:A选项中不共线的三条线段不一定首尾相接,不一定组成三角形,是随机事件;
B选项中一年最多366天,则400人中至少有2人生日在同一天,是必然事件;
C选项中太阳从西方升起是不可能事件;
D选项中打开电视不一定播放动画片,是随机事件;
故答案为:B
【分析】必然事件是指一定会发生或一定不会发生的事件;随机事件是指可能发生也可能不发生的事件.根据定义并结合各选项即可判断求解.
2.【答案】A
【解析】【解答】解:A、打开电视,正在播放《中国机长》,是随机事件,符合题意,选项正确;
B、白发三千丈,缘愁似个长,是不可能事件,不符合题意,选项错误;
C、离离原上草,一岁一枯荣,是必然事件,不符合题意,选项错误;
D、钝角三角形的内角和大于,是不可能事件,不符合题意,选项错误.
故答案为:A.
【分析】在一定条件下,可能发生,也可能不会发生的事件就是随机事件;在一定条件下,一定不会发生的事件就是不可能事件;在一定条件下,一定会发生的事件就是必然事件,根据定义即可一一判断得出答案.
3.【答案】D
【解析】【解答】解:A. “经过有交通信号的路口遇到红灯”是随机事件,故该选项不正确,不符合题意;
B. 已知某篮球运动员投篮投中的概率为,则他投次有可能可投中7次,故该选项不正确,不符合题意;
C. 明天太阳从东方升起是必然事件,故该选项不正确,不符合题意;
D. 投掷一枚硬币正面朝上是随机事件,故该选项正确,符合题意.
故答案为:D.
【分析】根据随机事件及概率的意义逐一判断即可.
4.【答案】B
【解析】【解答】解:由题意可得,×100%=80%,
解得,a=12.
故答案为:B.
【分析】利用白球的个数÷小球的总个数×100%=80%进行计算即可.
5.【答案】B
【解析】【解答】解:根据题意得:指针落在有阴影的区域内的概率为.
故答案为:B
【分析】利用几何概率公式的计算方法求解即可。
6.【答案】B
【解析】【解答】解:对方出“剪刀”.这个事件是是随机事件.
故答案为:B.
【分析】必然事件:在条件S下,一定会发生的事件,叫做相对条件S的必然事件,简称必然[
不可能事件:在条件S下,一定不可能发生的事件,叫做相对条件S的不可能事件,简称不可能事件;
随机事件:随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件.
7.【答案】D
【解析】【解答】解:抛一枚均匀硬币正面朝上的概率为,就是经过大量重复的实验,抛一枚均匀硬币正面朝上的频率越稳定在左右,因此,
A.通过抛一枚均匀硬币确定篮球赛中谁先发球是公平的,这是公平的,因此选项A不符合题意;
B.大量重复抛一枚均匀硬币,出现正面朝上的频率稳定于,这种说法是正确的,因此选项B不符合题意;
C.连续抛一枚均匀硬币10次可能都是正面朝上,是可能存在的,因此选项C不符合题意;
D.连续抛一枚均匀硬币2次必有1次正面朝上,这是不正确的,因此选项D符合题意;
故答案为:D.
【分析】根据概率的意义可判断A;根据频率估计概率的知识可判断B;根据随机事件的概念可判断C、D.
8.【答案】B
【解析】【解答】解:由表格数据,可知某一结果发生的概率约为0.33,
∵,,,,
∴与最接近的是,
∴该结果发生的概率约为.
故答案为:B
【分析】利用频率估算概率的计算方法求解即可。
9.【答案】B
【解析】【解答】解:由题意可知一共有5个数,奇数有3个,
∴P(抽取一张,其正面的数字是奇数)=.
故答案为:B
【分析】利用已知条件可得到所有等可能的结果数及从中随机抽取一张,其正面的数字是奇数的情况数,然后利用概率公式进行计算.
10.【答案】A
【解析】【解答】解:由题意可得:白球的个数为4,球的总数为6,
∴摸到白球的概率为.
故答案为:A.
【分析】利用白球的个数除以球的总数即可求出对应的概率.
11.【答案】5
【解析】【解答】解:∵一副扑克牌有13张红桃,甲有5张红桃牌,乙有4张红桃牌,
∴剩余4张红桃,
∴丁的红桃牌有0,1,2,3,4张五种不同的情况.
故答案为:5.
【分析】一副扑克牌有13张红桃,利用已知可得到剩余4张红桃,据此可得到丁的红桃牌的数量的不同情况.
12.【答案】0.9
【解析】【解答】解:由表可知:经过大量重复试验,成活的频率逐渐稳定到0.9,
∴该种幼树在此条件下移植成活的概率是0.9,
故答案为:0.9.
【分析】由表可知:经过大量重复试验,成活的频率逐渐稳定到0.9,然后根据频率估计概率的知识进行解答.
13.【答案】20
【解析】【解答】解:设估计袋中黄球的个数约为x个,根据题意得
解之:x=20.
故答案为:20
【分析】设估计袋中黄球的个数约为x个,根据经过多次试验发现摸到红球的频率稳定在0.2,可得到关于x的方程,解方程求出x的值.
14.【答案】16
【解析】【解答】解:∵抽中“十九届六中全会”字样的卡片的概率为,
∴,
解得n=16.
故答案为:16.
【分析】根据概率公式结合题意可得,求解即可.
15.【答案】解:(1),(2)可能发生,也可能不发生,是随机事件.
(3)一定不会发生,是不可能事件.
(4)一定发生,是必然事件.
【解析】【分析】根据正品、次品的只数可得:取出的3只可能为3只正品;也可能为1只次品、2只正品;2只次品,1只正品;根据次品的只数可知不可能取出3只次品;根据次品只数为2只可知一定会取出正品,据此解答.
16.【答案】解:由概率和频率公式可求得纸箱中国球的总数和红、白球的数目。如:
球总数=白球数目/白球频率=2525%=100 个
黄球数目=黄球频率球总数=40%100=40 个
红球数目=球总数-白球数目-黄球数目=100-25-40=35 个
则此题求得纸箱中红球35个,黄球40个。
【解析】【分析】本题若想求得红、黄球的数目,则需要先利用白球求出纸箱中的总球数,最后再求得红球和白球数目。
17.【答案】解:列表得:
小亮 小明 小伟
小丽 小丽,小亮 小丽,小明 小丽,小伟
小红 小红,小亮 小红,小明 小红,小伟
∵共有6种等可能的情况,而正好是男生小明和女生小红的有1种情况,
∴正好抽到男生小明和女生小红的概率= .
【解析】【分析】列表可确定共有6种情况,而正好是男生小明和女生小红的有1种情况,根据概率公式求解即可.
18.【答案】(1)10;40;90
(2)解:抽到八年级(5)班学生的可能性大小为:
【解析】【解答】解:(1)随机抽女生人数:4÷10%=40(名),即b=40;
A等级人数:40-24-4-2=10(名),即a=10;
扇形图中表示A的圆心角的度数360°× =90°
故答案为:10,40,90;
【分析】(1)根据C等级的人数和所占比例可知随机抽女生人数:4÷10%=40(名),即b=40;A等级人数:40-24-4-2=10(名),即a=10;扇形图中表示A的圆心角的度数360°× =90°;(2)根据概率公式求解即可.
19.【答案】(1)0.60
(2)0.6;0.4
(3)解:因为摸到白球的概率是0.6,摸到黑球的概率是0.4,
所以口袋中黑、白两种颜色的球有:
白球是只,
黑球是只.
答:估计口袋中白色的球有12只,黑色的球有8只.
【解析】【解答】解:(1)解:根据题意可得当很大时,摸到白球的频率将会接近0.60;
故答案为:0.60;
(2)解:因为当很大时,摸到白球的频率将会接近0.60;
所以摸到白球的概率是0.6;
摸到黑球的概率是0.4;
故答案为:0.6,0.4;
【分析】(1)根据表格中的信息可知:当n很大时,摸到白球的频率将会接近0.60;
(2)结合(1)的结论并根据用频率估计概率可求解;
(3)根据频数=概率×样本容量可求解.
20.【答案】(1)解:根据实验数量变大,发芽数也在增大,2850÷3000×100%=95%,
故该麦种的发芽概率约为95%;
(2)解:设约需麦种x千克,
x×1000÷50×1000×95%×80%=4000000×3,
化简得15200x=12000000,
解得x=789,
答:约需麦种790千克
【解析】【分析】(1)在大量的实验的前提下,用发芽频数除以实验种子数即可;
(2) 设约需麦种x千克, 根据麦种的粒数× 发芽概率 × 成秧率 =4000000×3,列出方程解之即可.
21.【答案】(1)
(2)解:
此事件共有12种情况,且可能性相等,其中抽取的这两张牌的牌面数字之和小于6的有6种情况,
∴
【解析】【解答】解:(1) 若随机抽取一张扑克牌,抽到数字4的概率为:,
故答案为:.
【分析】(1)根据概率公式计算求解即可;
(2)先画树状图,再求出此事件共有12种情况,且可能性相等,其中抽取的这两张牌的牌面数字之和小于6的有6种情况,最后求概率即可。
22.【答案】(1)5
(2)144
(3)40;40
(4)解:根据题意得:,
∴全校800名同学课外阅读时间不少于的人数为人.
【解析】【解答】(1)解:根据题意得:;
故答案为:5
(2)解:B组对应扇形的圆心角为;
故答案为:144
(3)解:阅读时间在范围内的数据中,40出现的次数最多,
∴阅读时间在范围内的数据的众数是;
把阅读时间在范围内的数据从小到大排列为:40,40,40,45,45,50, 50, 55,
∵,
∴调查的20名同学课外阅读时间位于正中间的两个数分别为40,40,
∴调查的20名同学课外阅读时间的中位数是;
故答案为:40;40
【分析】(1)用样本容量乘25%可得a的值,再用样本容量分别减去其他等级的频数可得b的值;
(2)用360°乘B等级所占比例即可;
(3)分别根据众数和中位数的定义解答即可;
(4)用800乘样本中课外阅读时间不少于40min的人数所占比例即可.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
