图形的相似单元测试题

绝密★启用前
第一章图形的相似试卷
考试范围：第一章图形的相似；考试时间：120分钟；命题人：李
第I卷（选择题）
一、选择题
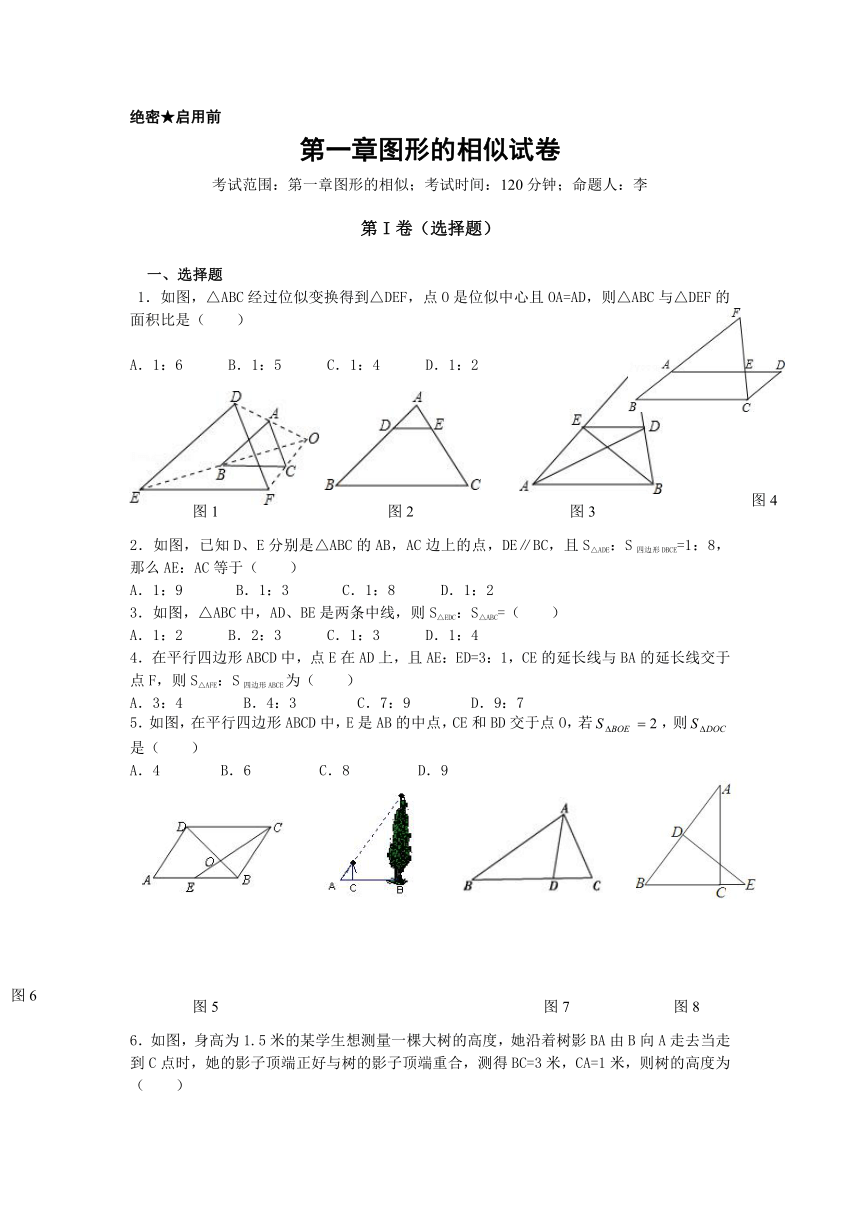
1．如图，△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，则△ABC与△DEF的面积比是（　　）
A．1：6 B．1：5 C．1：4 D．1：2
2．如图，已知D、E分别是△ABC的AB，AC边上的点，DE∥BC，且S△ADE：S四边形DBCE=1：8，那么AE：AC等于（　　）
A．1：9 B．1：3 C．1：8 D．1：2
3．如图，△ABC中，AD、BE是两条中线，则S△EDC：S△ABC=（　　）
A．1：2 B．2：3 C．1：3 D．1：4
4．在平行四边形ABCD中，点E在AD上 ( http: / / www.21cnjy.com )，且AE：ED=3：1，CE的延长线与BA的延长线交于点F，则S△AFE：S四边形ABCE为（　　）
A．3：4 B．4：3 C．7：9 D．9：7
5．如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点O，若，则是（ ）
A．4 B．6 C．8 D．9
6．如图，身高为1.5米的某学生想测量一棵 ( http: / / www.21cnjy.com )大树的高度，她沿着树影BA由B向A走去当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3米，CA=1米，则树的高度为（ ）
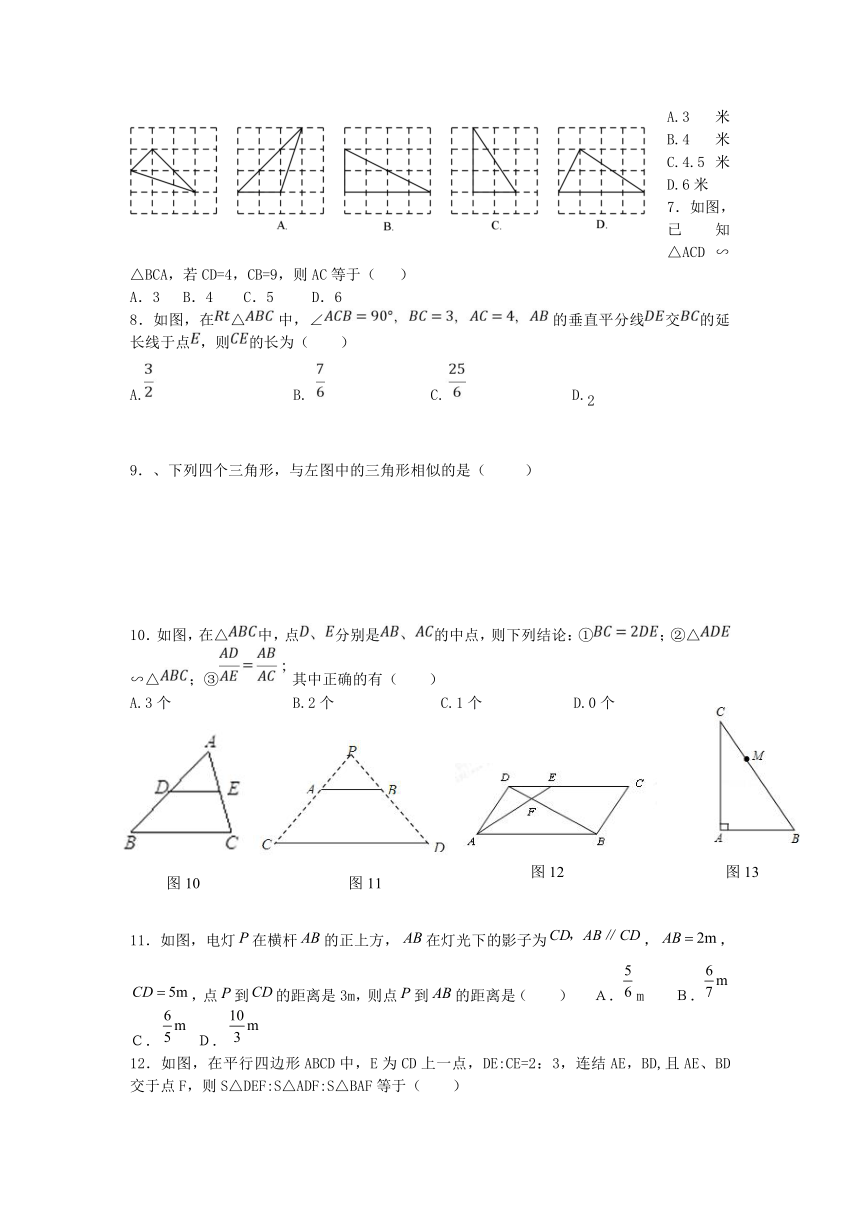
A.3米 B.4米 C.4.5米 D.6米
7．如图，已知△ACD∽△BCA，若CD=4，CB=9，则AC等于（ ）
A．3 B．4 C．5 D．6
8．如图，在△中，∠的垂直平分线交的延长线于点，则的长为（ ）
A. B. C. D.2
9．、下列四个三角形，与左图中的三角形相似的是（ ）
10．如图，在△中，点分别是的中点，则下列结论：①；②△∽△；③其中正确的有（ ）
A.3个 B.2个　　　 C.1个 D.0个
11．如图，电灯在横杆的正上方，在灯光下的影子为，，，点到的距离是3m，则点到的距离是（　　） Ａ．m Ｂ． Ｃ． Ｄ．
12．如图，在平行四边形ABCD中，E为C ( http: / / www.21cnjy.com )D上一点，DE:CE=2：3，连结AE，BD,且AE、BD交于点F，则S△DEF:S△ADF:S△BAF等于（　　）
A、4：10：25　 B、4：9：25 C、2：3：5 D、2：5：25
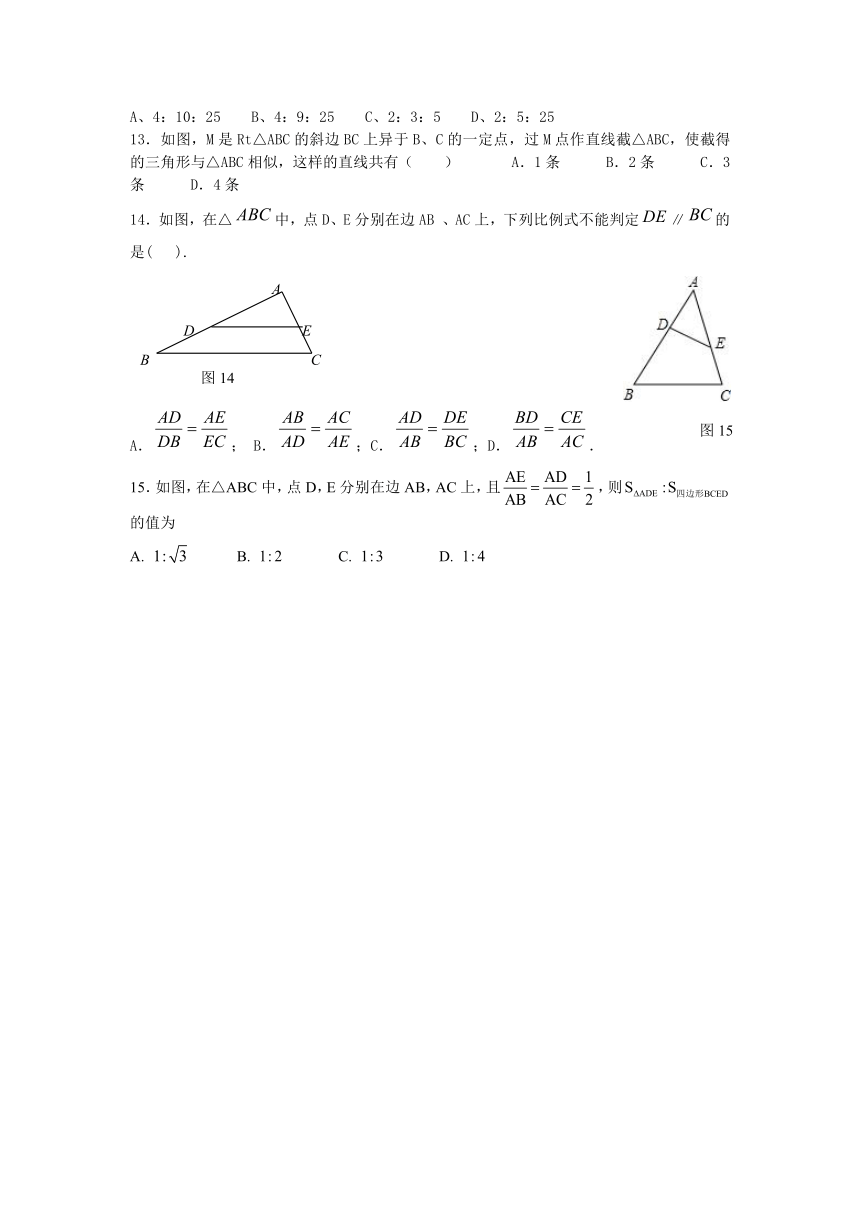
13．如图，M是Rt△AB ( http: / / www.21cnjy.com )C的斜边BC上异于B、C的一定点，过M点作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有（　　） A．1条 B．2条 C．3条 D．4条
14．如图，在△中，点D、E分别在边AB 、AC上，下列比例式不能判定∥的是( ).
A．； B．；C．；D．．
15．如图，在△ABC中，点D，E分别在边AB，AC上，且，则的值为
A. B. C. D.
第II卷（非选择题）
二、填空题（30分）
16．如图，直线l1∥l2∥l3，另两 ( http: / / www.21cnjy.com )条直线分别交l1、l2、l3于点A、B、C及点D、E、F，且AB＝3，DE＝4，DF＝6，则BC＝ ．
17．如图，平行于BC的直线DE把△ABC分成的两部分面积相等.则= .
18．如图，在平行四边形ABCD中，CD＝10，F是AB边上一点，DF交AC于点E，且＝，则＝________，BF＝________．
19．为了测量校园内一棵不可攀的树 ( http: / / www.21cnjy.com )的高度，学校数学应用实践小组做了如下的探索：根据光的反射定律，利用一面镜子和皮尺，设计如图所示的测量方案：把镜子放在离树(AB)8.7 m的点E处，然后观测者沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝2.7 m，观测者目高CD＝1.6 m，则树高AB约是________．(精确到0.1 m)
( http: / / www.21cnjy.com )
20．如图，已知，若再增加一个条件就能使结论“”成立，则这个条件可以是____________.（只填一个即可）
21．如图，△三个顶点的坐标分别为，以原点为位似中心，将△缩小，位似比为，则线段的中点变换后对应点的坐标为_________.
22．将一副三角尺如图所示叠放在一起，则的度数是 ，的值是 ．
三、计算题（15分）
23．（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE//BC，AQ交DE于点P,求证：
（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG,AF分别交DE于M,N两点.
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN=DM·EN
24．（12）已知：如图，在梯形A ( http: / / www.21cnjy.com )BCD中，AD∥BC，∠ABC=90°，BC=2AD，点E是BC的中点、F是CD上的点，联结AE、EF、AC．
（1）求证：AO OF=OC OE；
（2）若点F是DC的中点，联结BD交AE于点G，求证：四边形EFDG是菱形．
( http: / / www.21cnjy.com )
25．（12分）如图，△ABC中，BC >AC，点D在BC上，且CA=CD，∠ACB的平分线交AD于点F，E是AB的中点．
（1）求证：EF∥BD ；
（2）若∠ACB=60°，AC=8，BC=12，求四边形BDFE的面积．参考答案
1．C.
2．B．
3．D．
4．D
5．C.
6．D．
7．D.
8．B
9．C
10．A
11．C.
12．B.
13．C.
14．C
15．C。
16．1.5
17．.
18．　6
19．5.2 m
20．（答案不唯一）
21．或
22．75°,.
23．（1）证明略；（2）①，②证明略
24．(1)证明略；（2）证明略.
25．（1）证明略；（2）.
图4
图3
图2
图1
图6
图8
图7
图5
图13
图12
图10
图11
B
A
C
E
D
图14
图15
图18
图17
图16