四边形[下学期]
图片预览





文档简介
课件20张PPT。四边形2006(5)四边形
①探索并了解多边形的内角和与外角和公式,了解正多边形的概 念。
②掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性。
③探索并掌握平行四边形的有关性质[1]和四边形是平行四边形的条件[2]。 ’
④探索并掌握矩形、菱形、正方形的有关性质[3]和四边形是矩形、菱形、正方形的条件[4] 【备注2】:
[1]平行四边形的对边相等、对角相等、对角线互相平分。
[2]一组对边平行且相等,或两组对边分别相等,或对角线互相平分的四边形是平行四边形。
[3]矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直平分。 四边形
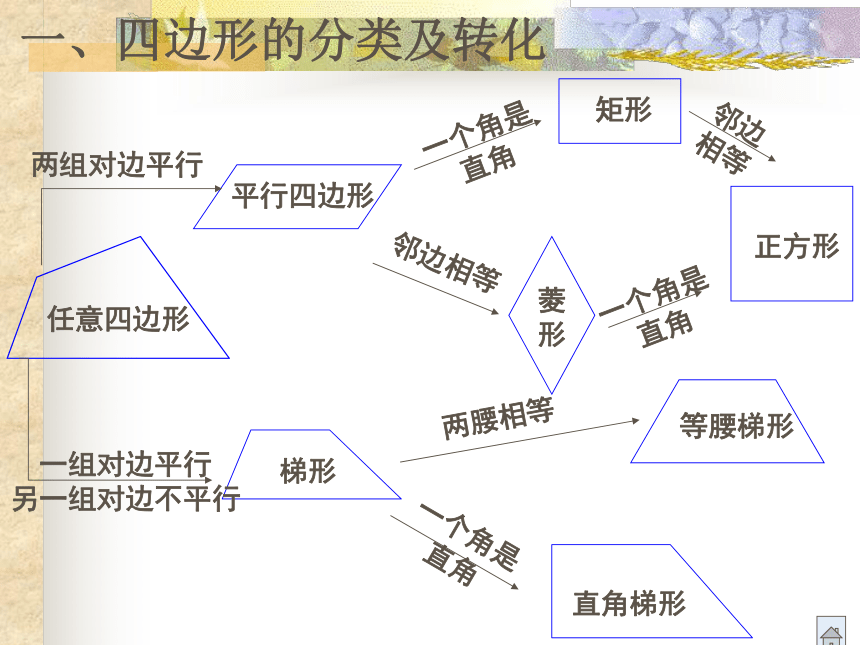
一、四边形的分类及转化
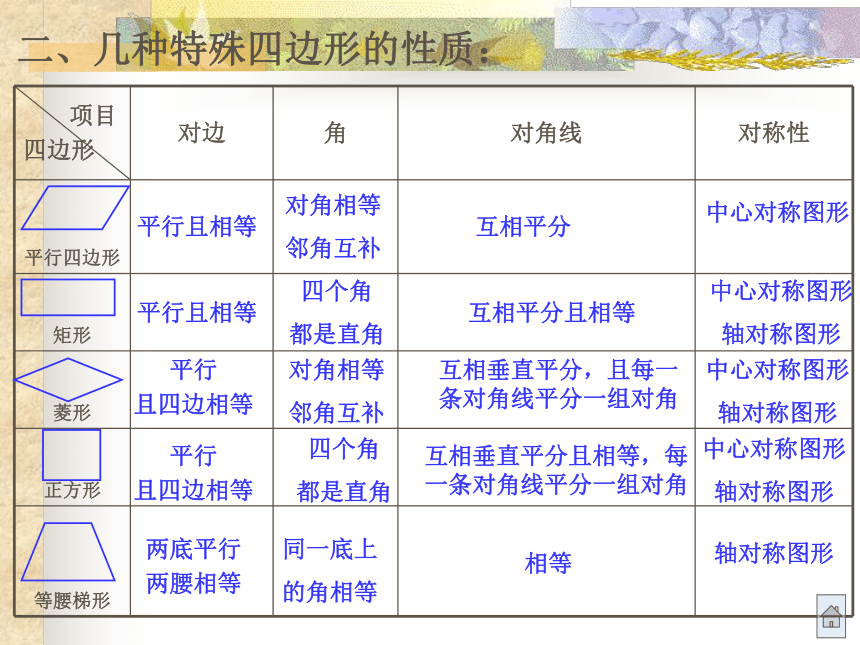
二、几种特殊四边形的性质
三、几种特殊四边形的常用判定方法
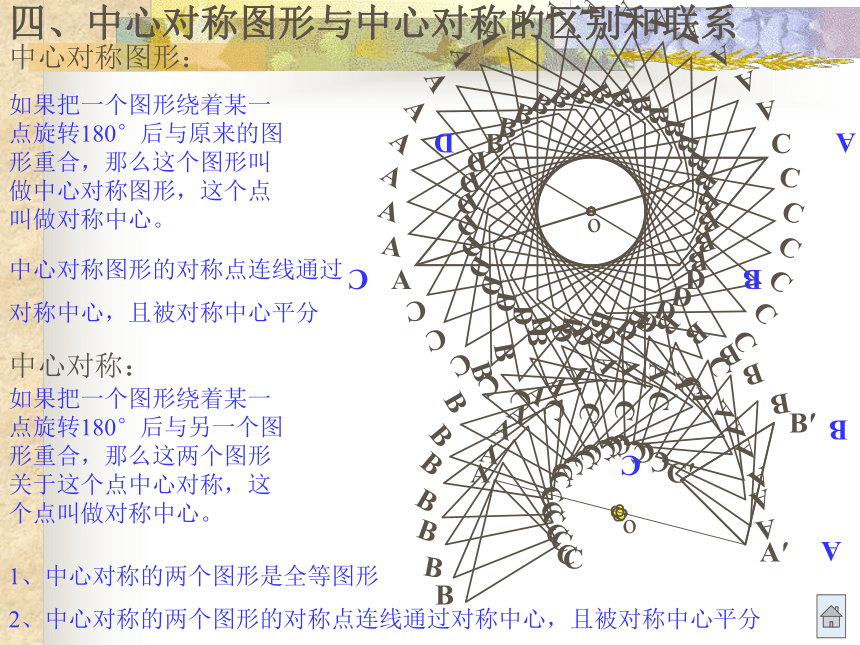
四、中心对称图形与中心对称的区别和联系
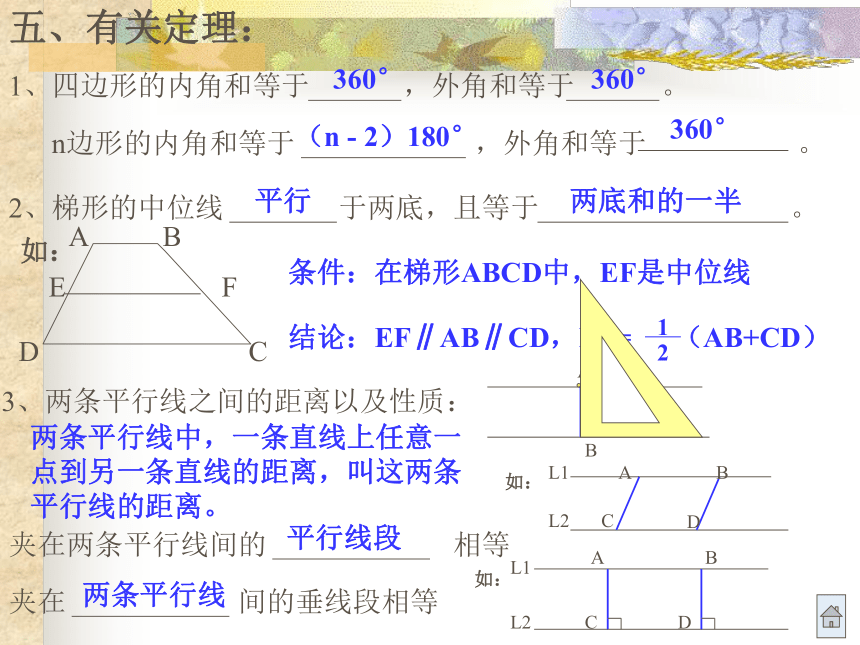
五、有关定理
六、主要画图
七、典型举例 一、四边形的分类及转化平行且相等平行且相等平行
且四边相等平行
且四边相等两底平行
两腰相等对角相等
邻角互补四个角
都是直角同一底上
的角相等对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分,且每一条对角线平分一组对角相等互相垂直平分且相等,每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形轴对称图形二、几种特殊四边形的性质:三、几种特殊四边形的常用判定方法:1、定义:两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分1、定义:有一外角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义:一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义:一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形1、两腰相等的梯形 2、在同一底上的两角相等的梯形 3、对角线相等的梯形四、中心对称图形与中心对称的区别和联系中心对称图形:中心对称:如果把一个图形绕着某一点旋转180°后与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心。如果把一个图形绕着某一点旋转180°后与另一个图形重合,那么这两个图形关于这个点中心对称,这个点叫做对称中心。C′A′B′1、中心对称的两个图形是全等图形
2、中心对称的两个图形的对称点连线通过对称中心,且被对称中心平分中心对称图形的对称点连线通过
对称中心,且被对称中心平分oo五、有关定理:平行360°(n - 2)180°360°两底和的一半360°条件:在梯形ABCD中,EF是中位线3、两条平行线之间的距离以及性质:平行线段两条平行线两条平行线中,一条直线上任意一点到另一条直线的距离,叫这两条平行线的距离。条件:AD∥BE∥CF,AB=BC结论:DE=EF条件:在△ABC中,AD= BD , DE∥BC结论:AE=EC条件:在梯形ABCD中,AE=DE ,AB∥EF∥DC结论:BF=FC相等第三边的中点另一腰的中点六、主要画图:1、画平行四边形、矩形、菱形、正方形、等腰梯形如:画一个平行四边形ABCD,使边BC=5cm,
对角线AC=5cm,BD=8cm.2、用平行线等分线段C如图:点C就是线段AB的中点如图:点D、E、F、H就是线段AB的五等分点七、典型举例:证明:四边形ABCD是平行四边形BE=DF四边形AFCE是平行四边形注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F例2:如图,在四边形ABCD中,AB=2,CD=1,∠A=60°, ∠B= ∠D=90 °,求四边形ABCD的面积。E注:四边形的问题经常转化为三角形的问题来解,转化的方法是添加适当的辅助线,如连结对角线、延长两边等。解:延长AD,BC交于点E,∵在Rt△ABE中,∠A=60°,∴∠E=30°又∵AB=2∵在Rt△CDE中,同理可得∴S四边形ABCD=S Rt△ABE - S Rt△CDE21例3:如图,在梯形ABCD中,AB∥CD,中位线EF=7cm,对角线AC⊥BD,∠BDC=30°,求梯形的高线AH析:求解有关梯形类的题目,常需添加辅助线,把问题转化为三角形或四边形来求解,添加辅助线一般有下列所示的几种情况:延长两腰M解:过A作AM∥BD,交CD的延长线于M又∵AB∥CD∴四边形ABDM是平行四边形,∴DM=AB,∠AMC= ∠BDC=30°又∵中位线EF=7cm,∴CM=CD+DM=CD+AB=2EF=14cm又∵AC⊥BD,∴AC⊥AM,∵AH⊥CD,∠ACD=60°注:①解“翻折图形”问题的关键是要认识到对折时折痕为重合两点的对称轴,会形成轴对称图形。
②本题通过设未知数,然后根据图形的几何元素间的关系列方程求解的方法,是数学中常用的“方程思想”。解:设折痕为EF,连结AC,AE,CF,若A,C两点重合,它们必关于EF对称,则EF是AC的中垂线 ,故AF=FC,设AC与EF交于点O,AF=FC=xcm答:折痕的长为7.5cm则FD=AD – AF=8 - x∴EF=±7.5(负根舍去)作FH⊥BC于H解法2同学们再见
①探索并了解多边形的内角和与外角和公式,了解正多边形的概 念。
②掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性。
③探索并掌握平行四边形的有关性质[1]和四边形是平行四边形的条件[2]。 ’
④探索并掌握矩形、菱形、正方形的有关性质[3]和四边形是矩形、菱形、正方形的条件[4] 【备注2】:
[1]平行四边形的对边相等、对角相等、对角线互相平分。
[2]一组对边平行且相等,或两组对边分别相等,或对角线互相平分的四边形是平行四边形。
[3]矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直平分。 四边形
一、四边形的分类及转化
二、几种特殊四边形的性质
三、几种特殊四边形的常用判定方法
四、中心对称图形与中心对称的区别和联系
五、有关定理
六、主要画图
七、典型举例 一、四边形的分类及转化平行且相等平行且相等平行
且四边相等平行
且四边相等两底平行
两腰相等对角相等
邻角互补四个角
都是直角同一底上
的角相等对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分,且每一条对角线平分一组对角相等互相垂直平分且相等,每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形轴对称图形二、几种特殊四边形的性质:三、几种特殊四边形的常用判定方法:1、定义:两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分1、定义:有一外角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义:一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义:一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形1、两腰相等的梯形 2、在同一底上的两角相等的梯形 3、对角线相等的梯形四、中心对称图形与中心对称的区别和联系中心对称图形:中心对称:如果把一个图形绕着某一点旋转180°后与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心。如果把一个图形绕着某一点旋转180°后与另一个图形重合,那么这两个图形关于这个点中心对称,这个点叫做对称中心。C′A′B′1、中心对称的两个图形是全等图形
2、中心对称的两个图形的对称点连线通过对称中心,且被对称中心平分中心对称图形的对称点连线通过
对称中心,且被对称中心平分oo五、有关定理:平行360°(n - 2)180°360°两底和的一半360°条件:在梯形ABCD中,EF是中位线3、两条平行线之间的距离以及性质:平行线段两条平行线两条平行线中,一条直线上任意一点到另一条直线的距离,叫这两条平行线的距离。条件:AD∥BE∥CF,AB=BC结论:DE=EF条件:在△ABC中,AD= BD , DE∥BC结论:AE=EC条件:在梯形ABCD中,AE=DE ,AB∥EF∥DC结论:BF=FC相等第三边的中点另一腰的中点六、主要画图:1、画平行四边形、矩形、菱形、正方形、等腰梯形如:画一个平行四边形ABCD,使边BC=5cm,
对角线AC=5cm,BD=8cm.2、用平行线等分线段C如图:点C就是线段AB的中点如图:点D、E、F、H就是线段AB的五等分点七、典型举例:证明:四边形ABCD是平行四边形BE=DF四边形AFCE是平行四边形注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F例2:如图,在四边形ABCD中,AB=2,CD=1,∠A=60°, ∠B= ∠D=90 °,求四边形ABCD的面积。E注:四边形的问题经常转化为三角形的问题来解,转化的方法是添加适当的辅助线,如连结对角线、延长两边等。解:延长AD,BC交于点E,∵在Rt△ABE中,∠A=60°,∴∠E=30°又∵AB=2∵在Rt△CDE中,同理可得∴S四边形ABCD=S Rt△ABE - S Rt△CDE21例3:如图,在梯形ABCD中,AB∥CD,中位线EF=7cm,对角线AC⊥BD,∠BDC=30°,求梯形的高线AH析:求解有关梯形类的题目,常需添加辅助线,把问题转化为三角形或四边形来求解,添加辅助线一般有下列所示的几种情况:延长两腰M解:过A作AM∥BD,交CD的延长线于M又∵AB∥CD∴四边形ABDM是平行四边形,∴DM=AB,∠AMC= ∠BDC=30°又∵中位线EF=7cm,∴CM=CD+DM=CD+AB=2EF=14cm又∵AC⊥BD,∴AC⊥AM,∵AH⊥CD,∠ACD=60°注:①解“翻折图形”问题的关键是要认识到对折时折痕为重合两点的对称轴,会形成轴对称图形。
②本题通过设未知数,然后根据图形的几何元素间的关系列方程求解的方法,是数学中常用的“方程思想”。解:设折痕为EF,连结AC,AE,CF,若A,C两点重合,它们必关于EF对称,则EF是AC的中垂线 ,故AF=FC,设AC与EF交于点O,AF=FC=xcm答:折痕的长为7.5cm则FD=AD – AF=8 - x∴EF=±7.5(负根舍去)作FH⊥BC于H解法2同学们再见
