等腰三角形的判定定理[上学期]

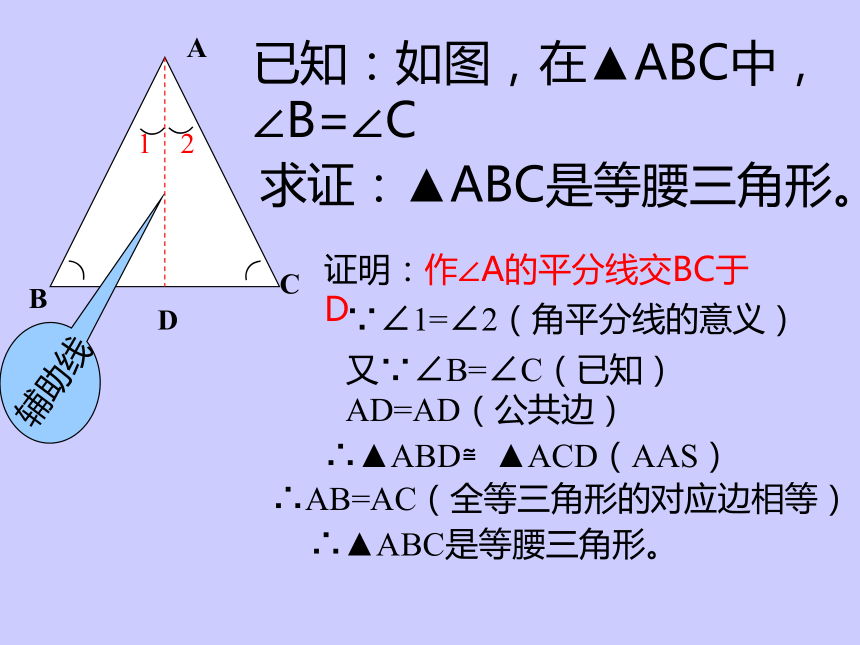
课件16张PPT。等腰三角形的判定定理主讲人：包淑婉复习等腰三角形的性质定理1、从边看：等腰三角形的两腰相等。（定义）2、从角看：等腰三角形的两底角相等。（性质定理1）3、从重要线段看：等腰三角形的顶角平分线、底边上的中线和高线互相重合。（性质定理2）定义：有两边相等的三角形是等腰三角形。如何判定一个三角形是等腰三角形？还有其他方法吗？等腰三角形的判定定理等腰三角形 的两底角相等，反之有两个角相等的三角形一定是等腰三角形吗？ABC⌒⌒⌒⌒12D已知：如图，在▲ABC中，∠B=∠C求证：▲ABC是等腰三角形。辅助线证明：作∠A的平分线交BC于D∵∠1=∠2（角平分线的意义）又∵∠B=∠C（已知）
AD=AD（公共边）∴▲ABD≌▲ACD（AAS）∴AB=AC（全等三角形的对应边相等）∴▲ABC是等腰三角形。等腰三角形的判定定理如果一个三角形有两个角相等，那么这个三角形是等腰三角形。(在一个三角形中，等角对等边。)应用格式：在▲ABC中
∵∠B=∠C（已知）
∴AB=AC（在一个三角形中，等边对等角）比一比等腰三角形的性质定理和判定定理的区别和联系？推论：三个角都相等的三角形是等边三角形。例1、已知：AD交BC于点O，AB‖CD，OA=OB
求证：OC=ODABCDO请你动手写一写！ABCDO提问1、若已知AB?CD，OC=OD，能否证明OA=OB？2、若已知OA=OB，OC=OD，能否证明AB?CD？AB?CD，OA=OB，OC=OD中已知任两个可推出第三个。规律：大家一起练一练1、求证：有一个叫是60o的等腰三角形是等边三角形。2、已知：如图，DE?BC，?1=?2。
求证：BD=CE。ADEBC分析：对于实际问题，关键在于把它转化为数学问题。
题目可改写成
已知：如图，AB=18?2=36海里
?A=40?，?NBC=80?
求BC的长。例2、如图，C表示灯塔，轮船从A处出发以每时18海里的速度向正北（AN方向）航行，2时后到达B处。测得C在A的北偏西40?方向，并在B的北偏西80?方向，求B处到灯塔C的距离。ABCN解：由已知，?NBC=80?，?A=40?∵ ? NB C=?A+?C（三角形的一个外角等于不相邻的两个内角和。）??C=?NBC–?A=80?–40?=40???A=?C?BA=BC（在一个三角形中，等边对等角）又∵BA=18?2=36海里?BC=36（海里）答：B处到灯塔C的距离是36海里。练习：如图1、已知：OD平分?AOB，EO=ED
求证：ED?OB。2、已知：OD平分?AOB，ED?OB
求证：EO=ED。3、已知：ED?OB，EO=ED
求证：OD平分?AOB。AEOBD规律：该图是有关等腰三角形的一个常用基本图形。“角平分线，平行线，等腰三角形”三者中，若有两者则必有第三者。想一想用七巧板拼成的图形（如图）中，有多少个是等腰直角三角形？小结：1、等腰三角形的判定方法（两种：定义，判定定理）2、等边三角形的判定方法（三种：定义，本节推论，本节练习1）3、等腰三角形的判定定理和性质定理的联系和区别。4、用等腰三角形的判定定理和性质定理证角相等或线段相等，
要求角或线段是同一个三角形中的内角或边；用三角形全等证
角相等或线段相等没有这个要求，但证明过程较复杂。请完成作业本中练习！再见