2023年江苏省无锡 九年级数学期末综合复习卷(一)(无答案)
文档属性
| 名称 | 2023年江苏省无锡 九年级数学期末综合复习卷(一)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 06:31:02 | ||
图片预览

文档简介
初三数学期末复习卷(一)
班级 姓名 学号 一、选择题(本大题共10小题,每题3分,共30分.)
1.已知x=1是一元二次方程x2-2mx+1=0的一个解,则m的值是 ( )
A. 1 B. 0 C. 0或1 D. 0或-1
2.若是一元二次方程x2―2x―3=0的两个根,则x1·x2的值是 ( )
A. B. C.4 D.
3.已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么下列结论正确的是( )
A.0<OP<5 B. OP=5 C. OP>5 D. OP≥5
4.二次函数y=x2+4x-5的图象的对称轴为 ( )
A.直线x=2 B.直线x=-2 C.直线x=4 D.直线x=-4
5.已知圆锥的底面半径为3cm,母线为5cm,则圆锥的侧面积是 ( )
A.30πcm2 B.15πcm2 C. cm2 D.10πcm2
6.已知在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是 ( )
A.sinA= B.tanA= C.cosB= D.tanB=
7.如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM︰OD=3︰5.则AB的长是( )
A.2cm B.3cm C.4cm D.2cm
8.如图,E是□ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是 ( )
A.= B.= C.= D.=
9.若函数的图象与坐标轴有三个交点,则的取值范围是 ( )
A. B. C. D.且
10.如图,在△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值是
(
(第
8
题)
(第
7
题)
(第
10
题)
(第
14
题)
)A.2 B. C. D.3― ( )
二、填空题(本大题共8小题,每题2分,共16分.)
11.方程x2=2x的根为 .
12.若x的一元二次方程kx2-2x-3=0有两个不相等的实数根,则k的取值范围是 .
13.若二次函数y=ax2-3x+a2-1的图象开口向下且经过原点,则a的值是 .
14.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD= .
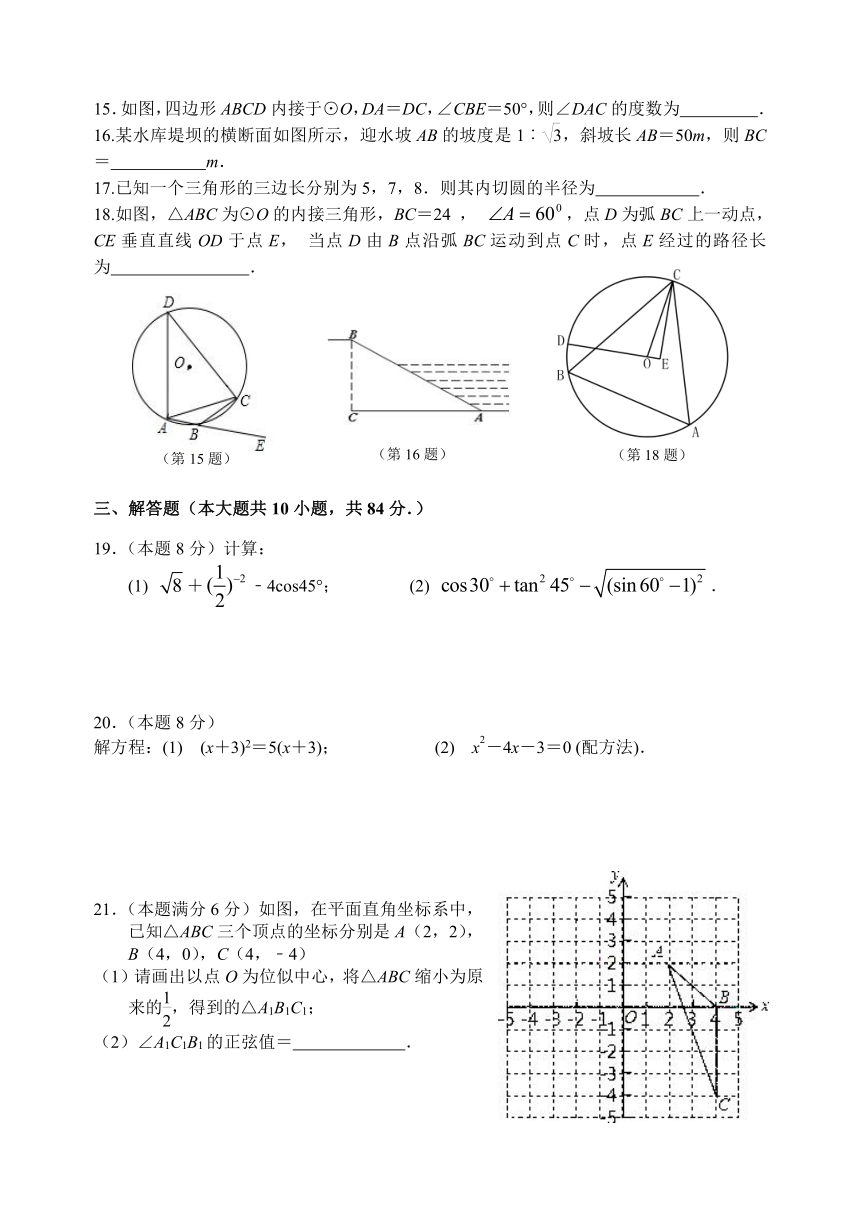
15.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的度数为 .
16.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1︰,斜坡长AB=50m,则BC= m.
17.已知一个三角形的三边长分别为5,7,8.则其内切圆的半径为 .
(
(第
16
题)
(第
15
题)
(第
18
题)
)18.如图,△ABC为⊙O的内接三角形,BC=24 , ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为 .
三、解答题(本大题共10小题,共84分.)
19.(本题8分)计算:
(1) +﹣4cos45°; (2) .
20.(本题8分)
解方程:(1) (x+3)2=5(x+3); (2) x-4x-3=0 (配方法).
21.(本题满分6分)如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出以点O为位似中心,将△ABC缩小为原来的,得到的△A1B1C1;
(2)∠A1C1B1的正弦值= .
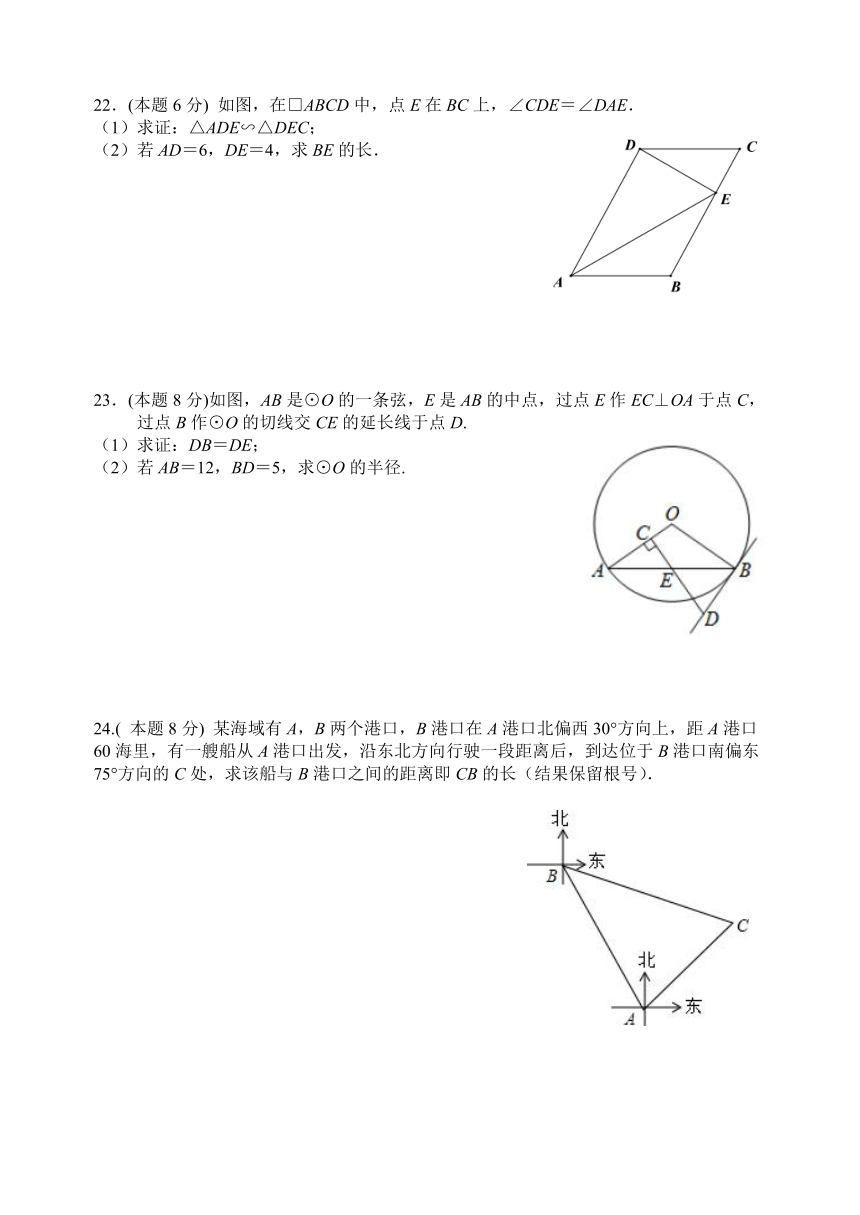
22.(本题6分) 如图,在□ABCD中,点E在BC上,∠CDE=∠DAE.
(1)求证:△ADE∽△DEC;
(2)若AD=6,DE=4,求BE的长.
23.(本题8分)如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
24.( 本题8分) 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
25.(本题10分)已知,如图,在Rt△ABC中,∠C=90 ,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹);
(2)判断直线BC与(1)中的⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O与AB边的另一个交点为E,AB=3,BD=,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和)
26.(本题10分)某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?
27.(本题10分)如图,抛物线与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
28.(本题10分)如图,已知一次函数的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
(1)求线段AB的长度;
(2)设点M在射线AB上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作⊙N.
①当⊙N与x轴相切时,求点M的坐标;
②在①的条件下,设直线AN与x轴交于点C,与⊙N的另一个交点为D,连接MD交x轴于点E,直线m过点N分别与y轴、直线l交于点P、Q,当△APQ与△CDE相似时,求点P的坐标.
.
班级 姓名 学号 一、选择题(本大题共10小题,每题3分,共30分.)
1.已知x=1是一元二次方程x2-2mx+1=0的一个解,则m的值是 ( )
A. 1 B. 0 C. 0或1 D. 0或-1
2.若是一元二次方程x2―2x―3=0的两个根,则x1·x2的值是 ( )
A. B. C.4 D.
3.已知⊙O的半径是5,直线l是⊙O的切线,P是l上的任一点,那么下列结论正确的是( )
A.0<OP<5 B. OP=5 C. OP>5 D. OP≥5
4.二次函数y=x2+4x-5的图象的对称轴为 ( )
A.直线x=2 B.直线x=-2 C.直线x=4 D.直线x=-4
5.已知圆锥的底面半径为3cm,母线为5cm,则圆锥的侧面积是 ( )
A.30πcm2 B.15πcm2 C. cm2 D.10πcm2
6.已知在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是 ( )
A.sinA= B.tanA= C.cosB= D.tanB=
7.如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM︰OD=3︰5.则AB的长是( )
A.2cm B.3cm C.4cm D.2cm
8.如图,E是□ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式中,错误的是 ( )
A.= B.= C.= D.=
9.若函数的图象与坐标轴有三个交点,则的取值范围是 ( )
A. B. C. D.且
10.如图,在△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值是
(
(第
8
题)
(第
7
题)
(第
10
题)
(第
14
题)
)A.2 B. C. D.3― ( )
二、填空题(本大题共8小题,每题2分,共16分.)
11.方程x2=2x的根为 .
12.若x的一元二次方程kx2-2x-3=0有两个不相等的实数根,则k的取值范围是 .
13.若二次函数y=ax2-3x+a2-1的图象开口向下且经过原点,则a的值是 .
14.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD= .
15.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的度数为 .
16.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1︰,斜坡长AB=50m,则BC= m.
17.已知一个三角形的三边长分别为5,7,8.则其内切圆的半径为 .
(
(第
16
题)
(第
15
题)
(第
18
题)
)18.如图,△ABC为⊙O的内接三角形,BC=24 , ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为 .
三、解答题(本大题共10小题,共84分.)
19.(本题8分)计算:
(1) +﹣4cos45°; (2) .
20.(本题8分)
解方程:(1) (x+3)2=5(x+3); (2) x-4x-3=0 (配方法).
21.(本题满分6分)如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出以点O为位似中心,将△ABC缩小为原来的,得到的△A1B1C1;
(2)∠A1C1B1的正弦值= .
22.(本题6分) 如图,在□ABCD中,点E在BC上,∠CDE=∠DAE.
(1)求证:△ADE∽△DEC;
(2)若AD=6,DE=4,求BE的长.
23.(本题8分)如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
24.( 本题8分) 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
25.(本题10分)已知,如图,在Rt△ABC中,∠C=90 ,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹);
(2)判断直线BC与(1)中的⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O与AB边的另一个交点为E,AB=3,BD=,求线段BD、BE与劣弧DE所围成的图形面积.(结果保留根号和)
26.(本题10分)某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?
27.(本题10分)如图,抛物线与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
28.(本题10分)如图,已知一次函数的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
(1)求线段AB的长度;
(2)设点M在射线AB上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作⊙N.
①当⊙N与x轴相切时,求点M的坐标;
②在①的条件下,设直线AN与x轴交于点C,与⊙N的另一个交点为D,连接MD交x轴于点E,直线m过点N分别与y轴、直线l交于点P、Q,当△APQ与△CDE相似时,求点P的坐标.
.
同课章节目录
