三角形内角和定理的证明与应用[下学期]
文档属性
| 名称 | 三角形内角和定理的证明与应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-07-16 17:50:00 | ||
图片预览






文档简介
课件28张PPT。三角形内角和的证明与应用 一、复习“三角形内角和定理” 我们已经知道:三角形的三个内角之和等于180゜。
即:在△ABC中, 有∠A+∠B+∠C=180゜
二、论证“三角形内角和定理” 即把∠A撕下来放在∠1的位置上,把∠B撕下来放在∠2的位置上。这时就可得∠ACB和∠1和∠2组成了一条直线,得到∠ACB+∠1+∠2=180゜,就可说明∠A+∠B+∠C=180゜了。 你试过了吗?. 在前面我们是采用拼接的方法来说明的。 但是组成的BC和CD真的就是一条直线吗?
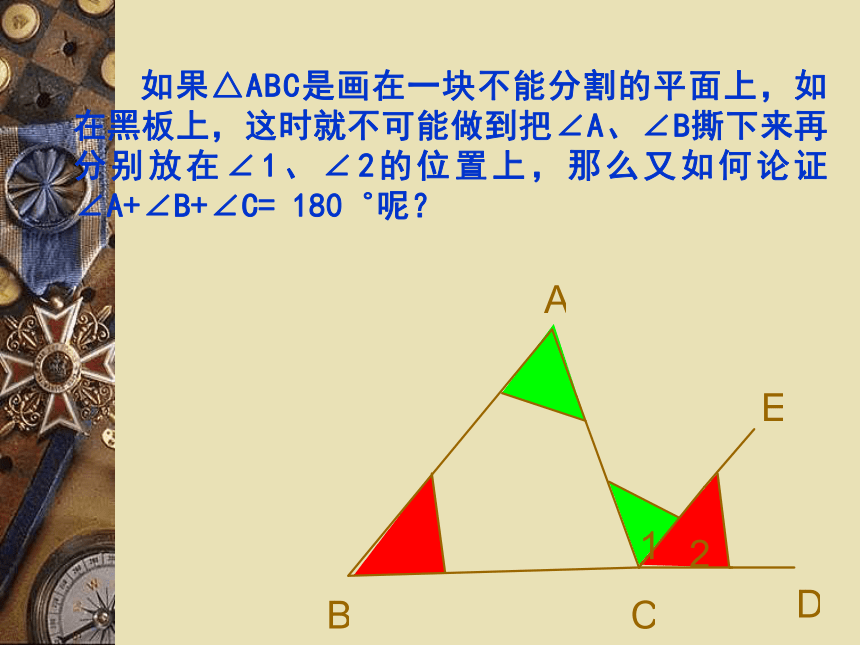
很明显,这是无法确定的 如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
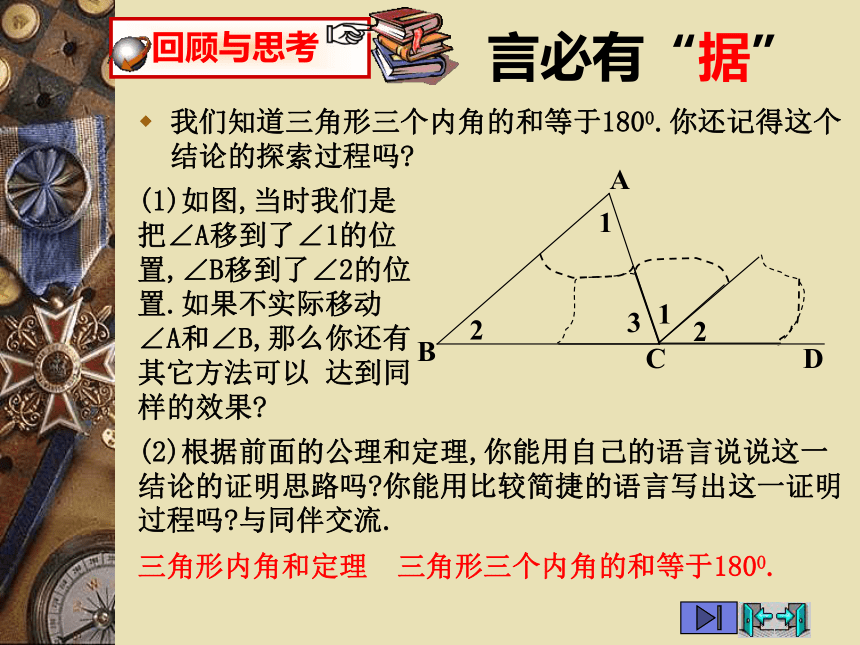
三角形内角和定理的证明 言必有“据”我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?12ABD3C(1)如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.如果不实际移动∠A和∠B,那么你还有其它方法可以 达到同样的效果?(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.三角形内角和定理 三角形三个内角的和等于1800.“行家” 看“门道”已知:如图, ∠A、∠B、∠C 是△ABC
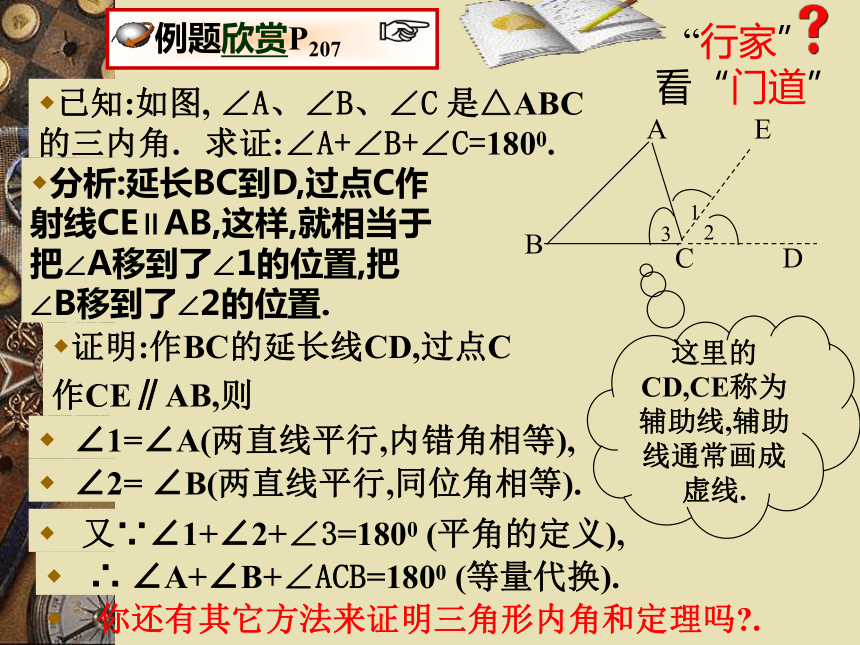
的三内角. 求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C
作CE∥AB,则 你还有其它方法来证明三角形内角和定理吗?. ∠1=∠A(两直线平行,内错角相等), ∠2= ∠B(两直线平行,同位角相等). 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.一题 多解在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请你帮小明把想法化为实际行动.小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则 ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等), 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.ABC已知:如图,△A B C.
求证:∠A +∠B +∠C=180°开启 智慧还有其他证明方法吗?“行家” 看“门道”根据下面的图形,写出相应的证明. 你还能想出其它证法吗?ABC证明:过A作AE∥BC,E开启 智慧证明:过点P作PQ ∥ AC交AB于Q点,
作PR ∥ AB交AC于R点。
∴四边形AQPR是平行四边形
(平行四边形的定义)
∴ ∠ QPR= ∠ A
(平行四边形的对角相等)
∠ RPC= ∠ B(两直线平行,同位角相等)
∠ QPB= ∠ C(两直线平行,同位角相等)
∵ ∠ QPB+ ∠ QPR + ∠ RPC=180 ° (1平角=180 ° )
∴ ∠ A+ ∠ B+ ∠ C=180 ° (等量代换)
∠EBC+ ∠FCB=180 °
(两直线平行,同旁内角互补)
即∠1+ ∠ABC+ ∠ACB+∠4= 180 °
又∵ ∠BAC= ∠2+ ∠3
∴ ∠BAC + ∠ABC + ∠ACB= 180 °
(等量代换)ABCEDF(((123证明:过A点作射线AD,过B点作BE ∥ AD,过C点作CF∥AD(两直线平行,内错角相等).4(则BE ∥ CF(平行与同一条直线的两直线平行)
∴∠1=∠2,∠3=∠4)A证明:E作BC的延长线CD,在△ABC的外部,以CA为一边, CE为另一边作∠1=∠A,则CE∥BA (内错角相等,两直线平行).∴∠B=∠2 (两直线平行,同位角相等).
)12又∵∠1+∠2+∠ACB=180° (平角的定义)∴∠A+∠B+∠ACB=180°
(等量代换)BCD O 在△ABC内任找一点O,连 接 AO、BO 、CO,即把△ABC分成三个三 角形,即△AOB、 △AOC、 △BOC,由于每个三角形的内角和相等,故可得等量关系△AOB、 △AOC 、△BOC 三个的内角和减去360就是△ABC 的内角和。 解:设△ABC的内角和 为 X , 于是有方程3X- 360° =X解得 X=180 °即三角形的内角和为180 ° O三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 我是最棒的1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500..结论: 直角三角形的两个锐角互余.以后可以直接运用.1、直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.ABC结论: 直角三角形的两个锐角互余;等边三角形每个内角60°以后可以直接运用.证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜(等量代换)
∴∠A+∠B=180゜-90゜= 90゜
(等式性质)
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜证明: ∵ DE ∥ BC (已知)
∴ ∠ AED= ∠ C(两直线平行,同位角相等)
∵ ∠ C=700(已知)
∴ ∠ AED= 700 (等量代换)
∵ ∠ A+ ∠ AED+ ∠ ADE=1800(三角形的内角和定理)
∠ A=600(已知)
∴ ∠ ADE=1800—600—700=500(等量代换)
即∠ ADE= 500(第2题)2、已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700. 求证: ∠ADE=5003、如图,直线AB∥CD,在AB、CD外有一点P,连结
PB、PD,交CD于E点。 则∠ B、 ∠ D、 ∠ P 之间是否存在一定的大小关系?他们是怎样的,并加以证明?用运动变化的观点理解和认识数学在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近1800),而∠B和 ∠C,越来越小(越来越接近00).由此你能想到什么?如果BC不动,把点A“拉离”BC,那么当A越来越远离BC时,∠A就越来越小(越来越接近00),而∠B和∠C则越来越大,它们的和越来越接近1800, 当把点A拉到无穷远时,便有AB∥AC,∠B和∠C成为同旁内角,它们的和等于1800.由此你能想到什么? 回味无穷掌握几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理.
结论: 直角三角形的两个锐角互余.
探索证明的思路的方法: 由“因”导“果”,执“果”索“因”.
与同伴交流,你是如何提高证明命题能力的. 我们证明了三角形内角和定理。证明的基本思想是:运用辅助线将原三角形中处于不同位置的三个内角集中在一起,拼成一个平角,辅助线是联系命题的条件和结论的桥梁。小结:本节课你有什么收获?三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 同学们你们掌握了吗,课后认真复习哦再见
即:在△ABC中, 有∠A+∠B+∠C=180゜
二、论证“三角形内角和定理” 即把∠A撕下来放在∠1的位置上,把∠B撕下来放在∠2的位置上。这时就可得∠ACB和∠1和∠2组成了一条直线,得到∠ACB+∠1+∠2=180゜,就可说明∠A+∠B+∠C=180゜了。 你试过了吗?. 在前面我们是采用拼接的方法来说明的。 但是组成的BC和CD真的就是一条直线吗?
很明显,这是无法确定的 如果△ABC是画在一块不能分割的平面上,如在黑板上,这时就不可能做到把∠A、∠B撕下来再分别放在∠1、∠2的位置上,那么又如何论证∠A+∠B+∠C= 180゜呢?
三角形内角和定理的证明 言必有“据”我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?12ABD3C(1)如图,当时我们是把∠A移到了∠1的位置,∠B移到了∠2的位置.如果不实际移动∠A和∠B,那么你还有其它方法可以 达到同样的效果?(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.三角形内角和定理 三角形三个内角的和等于1800.“行家” 看“门道”已知:如图, ∠A、∠B、∠C 是△ABC
的三内角. 求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C
作CE∥AB,则 你还有其它方法来证明三角形内角和定理吗?. ∠1=∠A(两直线平行,内错角相等), ∠2= ∠B(两直线平行,同位角相等). 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.一题 多解在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请你帮小明把想法化为实际行动.小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则 ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等), 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.ABC已知:如图,△A B C.
求证:∠A +∠B +∠C=180°开启 智慧还有其他证明方法吗?“行家” 看“门道”根据下面的图形,写出相应的证明. 你还能想出其它证法吗?ABC证明:过A作AE∥BC,E开启 智慧证明:过点P作PQ ∥ AC交AB于Q点,
作PR ∥ AB交AC于R点。
∴四边形AQPR是平行四边形
(平行四边形的定义)
∴ ∠ QPR= ∠ A
(平行四边形的对角相等)
∠ RPC= ∠ B(两直线平行,同位角相等)
∠ QPB= ∠ C(两直线平行,同位角相等)
∵ ∠ QPB+ ∠ QPR + ∠ RPC=180 ° (1平角=180 ° )
∴ ∠ A+ ∠ B+ ∠ C=180 ° (等量代换)
∠EBC+ ∠FCB=180 °
(两直线平行,同旁内角互补)
即∠1+ ∠ABC+ ∠ACB+∠4= 180 °
又∵ ∠BAC= ∠2+ ∠3
∴ ∠BAC + ∠ABC + ∠ACB= 180 °
(等量代换)ABCEDF(((123证明:过A点作射线AD,过B点作BE ∥ AD,过C点作CF∥AD(两直线平行,内错角相等).4(则BE ∥ CF(平行与同一条直线的两直线平行)
∴∠1=∠2,∠3=∠4)A证明:E作BC的延长线CD,在△ABC的外部,以CA为一边, CE为另一边作∠1=∠A,则CE∥BA (内错角相等,两直线平行).∴∠B=∠2 (两直线平行,同位角相等).
)12又∵∠1+∠2+∠ACB=180° (平角的定义)∴∠A+∠B+∠ACB=180°
(等量代换)BCD O 在△ABC内任找一点O,连 接 AO、BO 、CO,即把△ABC分成三个三 角形,即△AOB、 △AOC、 △BOC,由于每个三角形的内角和相等,故可得等量关系△AOB、 △AOC 、△BOC 三个的内角和减去360就是△ABC 的内角和。 解:设△ABC的内角和 为 X , 于是有方程3X- 360° =X解得 X=180 °即三角形的内角和为180 ° O三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 我是最棒的1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500..结论: 直角三角形的两个锐角互余.以后可以直接运用.1、直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.ABC结论: 直角三角形的两个锐角互余;等边三角形每个内角60°以后可以直接运用.证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜(等量代换)
∴∠A+∠B=180゜-90゜= 90゜
(等式性质)
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜证明: ∵ DE ∥ BC (已知)
∴ ∠ AED= ∠ C(两直线平行,同位角相等)
∵ ∠ C=700(已知)
∴ ∠ AED= 700 (等量代换)
∵ ∠ A+ ∠ AED+ ∠ ADE=1800(三角形的内角和定理)
∠ A=600(已知)
∴ ∠ ADE=1800—600—700=500(等量代换)
即∠ ADE= 500(第2题)2、已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700. 求证: ∠ADE=5003、如图,直线AB∥CD,在AB、CD外有一点P,连结
PB、PD,交CD于E点。 则∠ B、 ∠ D、 ∠ P 之间是否存在一定的大小关系?他们是怎样的,并加以证明?用运动变化的观点理解和认识数学在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近1800),而∠B和 ∠C,越来越小(越来越接近00).由此你能想到什么?如果BC不动,把点A“拉离”BC,那么当A越来越远离BC时,∠A就越来越小(越来越接近00),而∠B和∠C则越来越大,它们的和越来越接近1800, 当把点A拉到无穷远时,便有AB∥AC,∠B和∠C成为同旁内角,它们的和等于1800.由此你能想到什么? 回味无穷掌握几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理.
结论: 直角三角形的两个锐角互余.
探索证明的思路的方法: 由“因”导“果”,执“果”索“因”.
与同伴交流,你是如何提高证明命题能力的. 我们证明了三角形内角和定理。证明的基本思想是:运用辅助线将原三角形中处于不同位置的三个内角集中在一起,拼成一个平角,辅助线是联系命题的条件和结论的桥梁。小结:本节课你有什么收获?三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 同学们你们掌握了吗,课后认真复习哦再见
